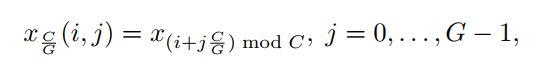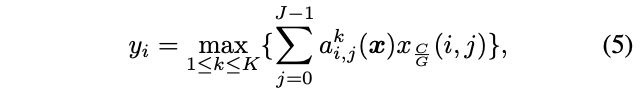轻量级网络MicroNet--低FLOPs的实现：卷积与激活函数的改进

论文地址：

《MicroNet: Towards Image Recognition with Extremely Low FLOPs》

亮点

卷积：稀疏连通性，避免了网络宽度的大幅度缩减；

激活函数：动态激活函数，减轻了网络深度缩减。

问题

这篇论文旨在以极低的计算成本解决性能大幅下降的问题，移动嵌入式设备通常具有较低的性能，因此要在边缘设备上部署深度学习模型，就要求网络模型具有较低计算量，但是低开销的网络通常性能表现不会很好。

高效CNN架构的最新进展成功地将ImageNet分类的计算成本从3.8G FLOPs (ResNet-50)降低了两个数量级到大约40M FLOPs（例如MobileNet、ShuffleNet），性能下降在可接受的范围内。

然而，当进一步降低计算成本时，它们会有显著的性能下降。例如，当计算成本分别从44M下降到21M和12M MAdds时，MobileNetV3的top-1准确率从65.4%大幅下降到58.0%和49.8%，而计算成本下降到4M MAdds时，MobileNetV3的top-1准确率下降到35.3%。

这篇论文提出了一种新的网络MicroNet，将极低 FLOP 机制下的精度从21M降到4M MAdds，这标志着计算成本降低到另一个数量级，而且性能下降在可接受的范围。 

设计原则

要想实现低FLOPs，主要是要限制网络宽度（输入输出通道数）和网络深度（网络结构层数），如果把一个卷积层抽象为一个层，那么该层输入和输出中间的连接边就可以用卷积核的参数量来衡量。

因此作者定义了卷积层连通性（connectivity）的概念，即每个输出节点所连接的边数。如果把一个卷积层的计算量设为固定值，那么更多的网络通道数就意味着更低的连通性：比如深度可分离卷积，具有较多的通道数但是有很弱的连通性。

作者认为平衡好通道数目和连通性之间的关系，避免减少通道数，可以有效地提升网络的容量。

作者认为当网络的深度（层数）大大减少时，其非线性性质会受到限制，从而导致明显的性能下降。

作者设计了MicroNet，针对上述问题提出了自己的设计原则如下：

1. MicroNet重新设计了卷积层的网络结构：降低网络节点（神经元）之间的连通性而不降低网络的宽度，Micro-Factorized convolution（微分解卷积）将MobileNet中的point-wise卷积以及depth-wise卷积分解为低秩矩阵，从而使得通道数目和输入输出的连通性得到一个良好的平衡；

2. MicroNet重新设计了一个激活函数：使用更复杂的非线性激活函数Dynamic Shift-Max来弥补通性网络深度的减少所带来的精度损失，使用一种新的激活函数，通过最大化输入特征图与其循环通道偏移之间的多重动态融合，来增强非线性特征；之所以称之为动态是因为融合过程的参数依赖于输入特征图。

Micro-Factorized Convolution（微分解卷积）

优化通道数和节点连接之间的trade-off；层之间的连通性E定义为每个输出节点的路径数，其中每条路径连接一个输入节点和一个输出节点。

Micro-Factorized Pointwise Convolution（微分解PW卷积）

作者提出使用分组自适应卷积来分解一个Pointwise卷积。其中分组数G自适应输入通道数C：

假设卷积核W具有相同数量的输入和输出通道C，R为通道压缩率，并忽略了bias。

对于常规的PW Conv，计算量很大为，为了进一步减少计算量，提升网络的稀疏性以降低连通性，论文作者将原始的稠密矩阵W分解为3个更加稀疏的矩阵P、Φ、Q'：

W是一个C×C矩阵；

Q是一个C×C/R矩阵，它将通道数压缩R倍；

P是一个C×C/R矩阵，它将通道数扩展回C；

Φ是一个C/R×C/R的置换矩阵，这个置换矩阵类似于shufflenet中的打乱通道顺序的操作； 

计算量为 

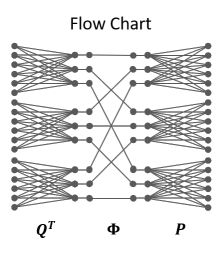
如下图所示：

其中C=18，R=2，所以G=3，原始PW卷积就需要一个18*18的实矩阵实现变换,计算量为324；

Q’将18个节点映射到9个节点（压缩率R为2），分为三组卷积，每组需要一个6*3的矩阵；

Φ将9个节点使用置换矩阵，进行重新排序；

P将9个节点分三组，映射回18个节点，每组需要一个3*6的矩阵;

计算量为O=2*18*18/2*3=108;

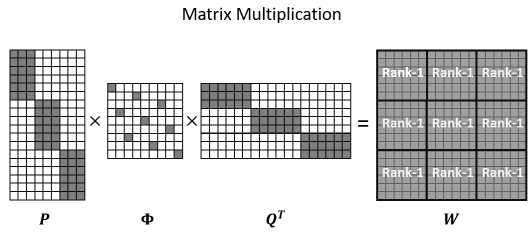
P和Q是带有G块的对角块矩阵，每个矩阵都实现了分组卷积实现，计算过程中矩阵的形态如下，其中P和Q为对角块矩阵，Φ为置换（排序）矩阵。分解后的3个矩阵的效果，相当于将原始W矩阵分成G*G个分组块，每个块的秩都为1。从节点的拓扑图可以看出网络是十分稀疏连的（非全连接），并且计算量也因此减少。

矩阵Φ的C/R通道表示为隐藏通道，而分组结构限制了这些通道的数量，每个隐藏通道连接到C/G个输入通道，每个输出通道连接到C/(RG)隐藏通道。每个输出通道的输入-输出连接数表示该层的连接；当计算预算和压缩因子R固定时，通道C和连通数E随G变化：

如图所示： 

 这两条曲线相交(即C=E)时，满足

 这个等式在通道数和节点连接性之间实现了很好的权衡，这保证了任何输入输出对之间不存在冗余路径（最小的路径冗余）和每对输入输出之间都存在一条路径（最大的输入覆盖率） ，从而使网络能够为给定的计算预算实现更多的通道。

这意味着分组数G的数量不是固定的，而是由通道数量C和压缩率因子R定义，该等式最优地平衡了通道数量C和输入/输出连通性E。数学上，得到的卷积矩阵W分解为G×G个秩为1的block。

Micro-Factorized Depthwise Convolution（微分解深度卷积）

引用Inception_v2中的分解卷积，将depthwize的一个K*K的卷积核分解为两个K*1和1*K的向量，将计算量从降到了2kC：

微分解PW卷积与微分解深度卷积结合得到Lite Combination

先用depthwise进行expand（通道数增加），再使用pointwise进行squeeze（通道压缩），这样可以节省更多的计算资源用到depthwise上，而非通道融合的pointwise上，如下图所示，先使用微分解的Depthwise卷积，通过对每个通道应用多个空间滤波器来扩展通道的数量，然后，应用一个分组自适应PW卷积来融合和压缩通道的数量。

Dynamic Shift-Max

使用一种新的激活函数，通过最大化输入特征图与其循环通道偏移之间的多重动态融合，来增强非线性特征，用于加强由Micro-Factorized创建的组之间的联系。 

假设为输入的第i个通道的特征图，则定义第i个通道在第j个组上的组循环偏移函数如下：（C为输入通道数，G为分组数）

动态最大偏移函数（Dynamic Shift-Max）如下：

其中J表示组数，i表示通道数，K表示融合后的输出数量J和K为手工设置的超参数，一般设置J=K=2；是可学习参数，并且是依赖于输入样本x的动态参数，类似于SENet中的动态通道加权，动态参数可以简单地通过两个全连接层后加平均池化层实现。

即每J个组，对每组的x进行加权求和，共K个融合，然后取K个中的最大值作为第i个通道上的激活函数值。 

Dynamic Shift-Max实现了两种形式的非线性：

1. 输出J组的K个融合的最大值，是对侧重于每一组内的连通性的微分解pointwise卷积的补充，从而加强了每一组之间的连接；
2. 通过一个动态参数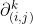、来加权每个融合，使网络能够根据输入样本x来调整这种增强功能；

这两种非线性增加了网络的表示能力，弥补了减少的层数所固有的损失。

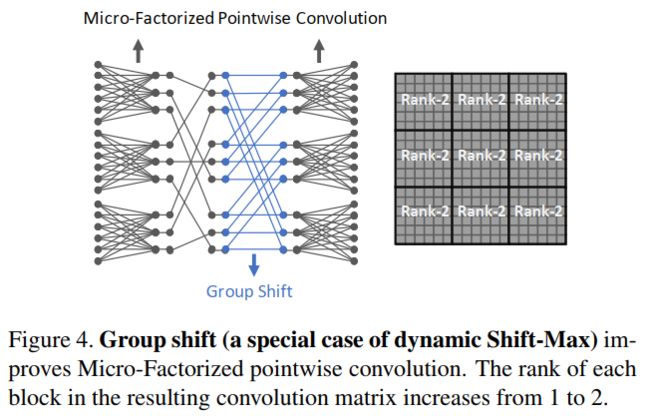
如下图所示，为使用Dynamic Shift-Max改装后的Micro-Factorized Pointwise Convolution（K=1，J=2）,在置换矩阵Φ之后又添加了Group Shift映射，来实现2个通道的信息融合（其中输出每个节点都来自两个不同输入组节点的映射）。通过添加Dynamic Shift-Max激活函数，卷积矩阵W中9个子矩阵块的秩从1上升到了2，提高了连通性。

Micro-Blocks 

作者介绍了3种不同MicroNet模型，其计算量FLOPs从6M到44M；

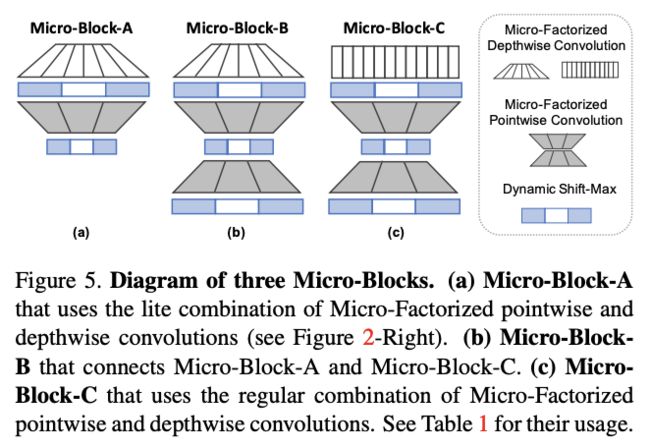
它们都是由 Micro-Factorized Pointwise Convolution 和 Micro-Factorized Depth-wise Convolution以不同的形式组合而来，并且都使用Dynamic Shift-Max作为激活函数。

图（a）所示：Micro-Block-A使用了微分解的pointwise和depthwise卷积的lite组合，通过微分解的depthwise卷积扩展了通道的数量，并通过分组自适应PW卷积进行压缩，对分辨率较高的低维特征特别有效；

图（b）所示：在Micro-Block-A基础上加了一个 MicroFactorized pointwise convolution进行维度扩展，包括两个分组自适应PW卷积：前者压缩了通道数量，而后者则增加了通道数量；

图（c）所示：Micro-Block-C实现了微分解的pointwise卷积和depthwise卷积的常规组合，它最适合于更高的网络层，因为它比精简组合为通道融合分配更多的计算。

每个block有四个超参数：卷积核大小k、输出通道数C、Micro-Factorized pointwise瓶颈处的缩减比R、2个Group自适应PW卷积的Group数对(G1,G2)。

网络结构

不同参数和计算量的MicroNet实例化结构：

需要注意的是两种卷积的分组数G1和G2，论文将分数组G的计算公式G=的约束G1G2改为C/R。

作者重新设计了Stem层，以满足低FLOPs的约束。它包括一个1*3的卷积和一个3*1的群卷积，然后是一个ReLU，第2次卷积将通道的数量增加了R倍。这大大节省了计算成本。

实验 

1. From MobileNet to MicroNet

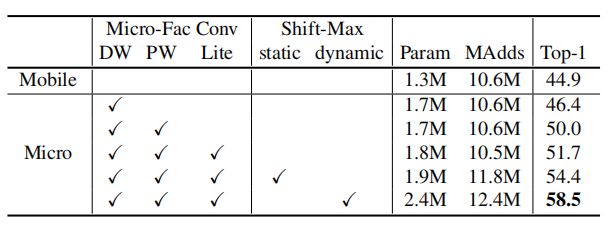
下表展示了从MobileNet到MicroNet的改变过程，表明Micro-Factorized卷积和Dynamic Shift-Max都是在计算成本极低的情况下实现网络的有效和互补的机制。

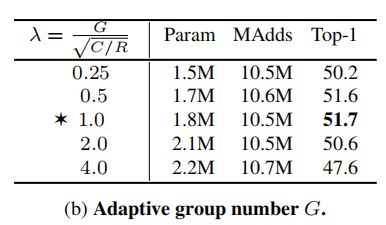
2. Number of Groups G 

下表展示了固定分组和自适应分组的对比，表明分组自适应卷积获得了更高的精度，证明了其在输入输出连接性和通道数之间的最优权衡的重要性， 可以看出，λ = 1时的效果最好。 

3. Lite combination

下表展示了使用微分解pointwise和depthwise卷积的lite组合在网络高低层进行比较。可以看出，lite组合对低层更有效。

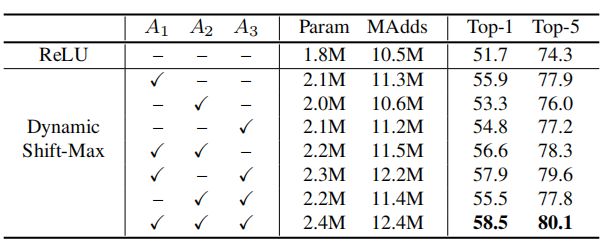
4. Activation functions 

下表展示了Dynamic Shift-Max与以前的三个激活函数进行比较。可以看出，Dynamic Shift-Max在性能上更好。

5. Location of Dynamic Shift-Max 

下表展示了不同位置的DY-Shift-Max的精度。可以看出，在所有结构中都使用DY-Shift-Max时，精度最高。

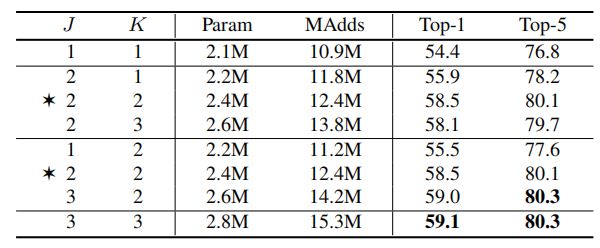
6. Hyper-parameters in Dynamic Shift-Max:

 下表展示了不同超参J和K的结果，可以看出，J=K=2时效果比较均衡。

总结 

这篇论文的目的是设计一个极低运算量但是网络性能不下降太多的网络结构，向着更轻量化前进，因为轻量化网络更容易在现实项目落地；

MicroNet主要的创新点在于：

通过分解DW与PW卷积核，压缩网络的连接性，使网络连接稀疏化，提高计算性能；

设计了全新的动态激活函数，引入更多的非线性特征，增强模型表现力。

参考

稀疏连接的 MicroNet

更小更快更好的MicroNet 

MicroNet: 低秩近似分解卷积以及超强激活函数 

MicroNet通过极低FLOPs实现图像识别 

 

仅为学习记录，侵删！