算法设计与分析2022 · 云端实验库
等我写完快排实验我才发现实验1是二分搜索不是快速排序tnnd都写完了舍不得删
敢于斗争,不怕牺牲
0-快速排序-递归
分析论
1.宏观视角:递归算法,每次将[l,r]区间进行快速排序,并向下递归
2.算法思想
A.极限划分返回:只有一个元素(或溢出)的时候返回
B.中间参考值划分:
中间参考值x,s1 s2左右指针,不断向中间位置靠拢
把大的丢右边去,小的丢左边去
如果s1,s2还没有交叠时候跳出
C.debug注意事项:边界问题
类似于二分搜索算法,受制于int向下取整的特性,l+r>>1可能会损失精度
对于除以2应当分为两种情况【向下取整 l+r>>1】【向上取整 l+r+1>>1】
这会影响到 向下递归时 子区间的划分
最终跳出while时候,s1到mid右侧,s2到mid左侧;此时要思考mid踩在哪个s上
这个我也不知道怎么说,看大家自己的悟性,我是这么理解的
这是我在整数二分搜索中参悟的思想
代码区
#include
#include
#include
using namespace std;
const int N = 1e5 + 7;
int node[N], n;
void asd(int a[], int l, int r)
{
if (l >= r)
return;
int x = a[l + r >> 1], s1 = l - 1, s2 = r + 1;
while (s1 < s2)
{
while (a[++s1] < x)
; //左侧靠近
while (a[--s2] > x)
; //右侧靠近
if (s1 < s2)
swap(a[s1], a[s2]); //没有溢出
}
// printf("%d %d \n", s1, s2);
asd(a, l, s2), asd(a, s2 + 1, r);
}
//如果是从大到小排序,只要改一下两个while中的符号就可以了
//不要去调整s1,s2
//思想上和二分查找是一脉相承的
/* S1左向右,S2右向左;最终数轴位置 S2在左S1在右
l+r 除以2,那么 mid踩在靠左侧 R 【左侧S2】【右侧S2+1】
l+r+1除以2 那么 mid踩在靠右侧 L 【左侧S1-1】【右侧S1】
*/
int main()
{
//输入
scanf("%d", &n);
for (int x = 0; x < n; x++)
scanf("%d", &node[x]);
//排序
asd(node, 0, n - 1);
//输出
for (int x = 0; x < n; x++)
printf("%d ", node[x]);
return 0;
}
/*
样例:对于取【中间点】【边界点】
10
49 59 88 37 98 97 68 54 31 3
样例:对于【do while】格式修改的;超时
30
128 294 133 295 175 8 232 248 241 164 11 60
238 133 291 116 6 67 98 67 196 260 181 160 83 160 90 153 233 216
*/
/*o(nlogn)
速度快,但是不稳定(相同数值的相对位置在排序前后或发生变化)
额外空间小,容易实现,书写简单(唯一的缺点)
*/
/*改S1报错
10
49 59 88 37 98 97 68 54 31 3
*/ 0-快速排序-非递归
分析论
使用queue临时存一下l和r,先进去的一定是【大区间】,向下递归的【小区间】存后边
网上找代码真是太难受了,写的又复杂又不直观,学习思想后自己写更舒服
queue是从宏观到微观,宏观工作完成了才会向下递归(弹出queue)
不能使用stack,因为他会在【没有完成工作】的情况下探底
代码区-queue
#include
#include
#include
#include
#include
using namespace std;
const int N = 1e5 + 7;
int b[N], n;
void qsort(int *a, int l, int r)
{
queue q;
//用于存放等待排序的左右指针
//首发入阵
q.push(l), q.push(r);
//先做一次左右排序,然后转入queue
while (q.size()) //非空的时候,依次弹出
{
l = q.front(), q.pop();
r = q.front(), q.pop();
if (l >= r)
continue;
int s1, s2, x;
s1 = l - 1, s2 = r + 1;
x = a[l + r >> 1]; //取得中间数值
while (s1 < s2)
{
// printf("%d %d\n", s1, s2);
while (a[++s1] < x)
;
while (a[--s2] > x)
;
if (s1 < s2)
swap(a[s1], a[s2]);
}
q.push(l), q.push(s2), q.push(s2 + 1), q.push(r);
}
}
void show(int *a)
{
// puts("233");
for (int i = 0; i < n; i++)
printf("%d ", a[i]);
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i++)
scanf("%d", &b[i]);
qsort(b, 0, n - 1);
show(b);
return 0;
} 1-二分搜索-非递归
分析论
思想过程:【追寻左端点】
1.宏观lr步数,查询t输入
2.while,lr没有交叠
A.mid=l+r>>1(暂定)
思想论:从不满足性质的一侧开始找,部署【首个满足条件元素具有的性质】
(左侧开始找,递增,找首个>=)
应该说左侧都是小的数字,右侧都是大的数字
B.关于 a[mid]的判断
a.首个满足性质的部署mid
思想论:mid满足性质,说明落在了右区间,我们要寻找的左端点应该在左区间找
向下取整时:左区间[l,mid] 右区间[mid+1,r]
向上取整时:左区间[l,mid-1] 右区间[mid,r]
跳出循环时候交叠,r在左侧,l在右侧
b.思考1:r=mid(mid在右区间,我们要去左区间找,所以更新【左区间的右端点r】)
c.反推1:l=mid+1
d.反推2:l+r>>1
思想论:mid踩在左侧r说明向下取整不用+1,mid踩在右侧l说明向上取整需要+1
这里S2就是R,S1就是L,跳出while时候说明左右指针交叠了
结束的时候看一下a[l],不相等说明这玩意压根就不存在
我们的追踪方法会让l停留在【首个满足该性质的元素】位置上
思想过程:【追寻右端点】
1.宏观lr步数,查询t输入
2.while,lr没有交叠
A.mid=l+r>>1(暂定)
思想论:从不满足性质的一侧开始找,部署【首个满足条件元素具有的性质】
(左侧开始找,递增,找首个>=) 应该说左侧都是小的数字,右侧都是大的数字
B.关于 a[mid]的判断
a.首个满足性质的部署mid
思想论:mid满足性质,说明落在了左区间,我们要寻找的右端点应该在右区间找
向下取整时:左区间[l,mid] 右区间[mid+1,r]
向上取整时:左区间[l,mid-1] 右区间[mid,r]
跳出循环时候交叠,r在左侧,l在右侧
b.思考1:l=mid(mid在左区间,我们要去右区间找,所以更新【右区间的左端点l】)
c.反推1:r=mid-1
d.反推2:l+r+1>>1
思想论:mid踩在右侧l说明向上取整,需要+1
代码区-非递归切分
#include
#include
#include
using namespace std;
const int N = 1e5 + 7;
int n, m, a[N];
//《模板示例》
//更新边界R在左侧,L在右侧
//[l,mid]-->r=mid (左侧) l=mid+1
//[mid,r]-->l=mid (右侧) r=mid-1
/*
二分搜索,应用于具有单调性的序列之中
现有一串不减序列,给到n个数字和m个询问
数组内编号0~n-1
输出所询问数字的启止范围
如果不存在输出-1 -1
*/
bool check(int a)
{ //满足性质的mid处在【左右】哪个区间
return true;
}
int T1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1; //无需+1型,mid在R位置
if (check(a[mid])) //此时满足的mid在右边区间,答案在左区间,更新R(左区间的右端点)
r = mid;
else
l = mid + 1;
}
return l;
}
int T2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1; //无需+1型,mid在R位置
if (check(a[mid])) //此时满足的mid在左边区间,答案在右区间,更新L(右区间的左端点)
l = mid;
else
r = mid - 1;
}
return l;
}
int main()
{
scanf("%d%d", &n, &m);
for (int x = 0; x < n; x++)
scanf("%d", &a[x]);
int t;
while (m--)
{
scanf("%d", &t);
int l = 0, r = n - 1;
while (l < r) //寻找左侧出发点
{
int mid = l + r >> 1;
if (a[mid] >= t)
r = mid;
else
l = mid + 1;
}
if (a[l] != t) //首次搜索都搜不到说明根本没有
{
printf("-1 -1\n");
continue;
}
printf("%d ", l); //否则,得出起始位置
l = 0, r = n - 1; //寻找右侧终止点
while (l < r)
{
int mid = l + r + 1 >> 1;
if (a[mid] <= t)
l = mid;
else
r = mid - 1;
}
printf("%d\n", r);
}
return 0;
}
/*
思想过程:【追寻左端点】
1.宏观lr步数,查询t输入
2.while,lr没有交叠
A.mid=l+r>>1(暂定)
思想论:从不满足性质的一侧开始找,部署【首个满足条件元素具有的性质】(左侧开始找,递增,找首个>=)
应该说左侧都是小的数字,右侧都是大的数字
B.关于 a[mid]的判断
a.首个满足性质的部署mid
思想论:mid满足性质,说明落在了右区间,我们要寻找的左端点应该在左区间找
向下取整时:左区间[l,mid] 右区间[mid+1,r]
向上取整时:左区间[l,mid-1] 右区间[mid,r]
跳出循环时候交叠,r在左侧,l在右侧
b.思考1:r=mid(mid在右区间,我们要去左区间找,所以更新【左区间的右端点r】)
c.反推1:l=mid+1
d.反推2:l+r>>1
思想论:mid踩在左侧r说明向下取整不用+1,mid踩在右侧l说明向上取整需要+1
结束的时候看一下a[l]不相等说明这玩意压根就不存在
我们的追踪方法会让l停留在【首个满足该性质的元素】位置上
思想过程:【追寻右端点】
1.宏观lr步数,查询t输入
2.while,lr没有交叠
A.mid=l+r>>1(暂定)
思想论:从不满足性质的一侧开始找,部署【首个满足条件元素具有的性质】(左侧开始找,递增,找首个>=)
应该说左侧都是小的数字,右侧都是大的数字
B.关于 a[mid]的判断
a.首个满足性质的部署mid
思想论:mid满足性质,说明落在了左区间,我们要寻找的右端点应该在右区间找
向下取整时:左区间[l,mid] 右区间[mid+1,r]
向上取整时:左区间[l,mid-1] 右区间[mid,r]
跳出循环时候交叠,r在左侧,l在右侧
b.思考1:l=mid(mid在左区间,我们要去右区间找,所以更新【右区间的左端点l】)
c.反推1:r=mid-1
d.反推2:l+r+1>>1
思想论:mid踩在右侧l说明向上取整,需要+1
*/ 1-二分搜索-递归
分析论
稍微改造一下就可以了,思路和上边是一样的,只是while控制改成边缘返回条件罢了
同样通过了ACWING的测试
代码区-递归切分
#include
#include
#include
using namespace std;
const int N = 1e5 + 7;
int n, m, a[N], t;
int getL(int t, int l, int r)
{
if (l >= r)
return l;
int mid = l + r >> 1;
if (a[mid] >= t)
getL(t, l, mid);
else
getL(t, mid + 1, r);
}
int getR(int t, int l, int r)
{
if (l >= r)
return r;
int mid = l + r + 1 >> 1;
if (a[mid] <= t)
getR(t, mid, r);
else
getR(t, l, mid - 1);
}
int main()
{
scanf("%d%d", &n, &m);
for (int x = 0; x < n; x++)
scanf("%d", &a[x]);
while (m--)
{
scanf("%d", &t);
int l = getL(t, 0, n - 1);
if (a[l] != t)
{
printf("-1 -1\n");
continue;
}
int r = getR(t, 0, n - 1);
printf("%d %d\n", l, r);
}
return 0;
} 2-最大子段和-暴力
分析论 带了个前缀和
代码区
#include
#include
#include
using namespace std;
#define LL long long
const int N = 1e5 + 7;
int n, a[N];
LL maxx=-2e9, b[N];
//堆栈外区不用初始化默认就是0,并且可以开更大的数组
// main里面数组不能太大,并且
void t1()
{
scanf("%d", &n);
for (int i = 0; i < n; i++)
scanf("%d", &a[i]);
for (int e = 0; e < n; e++)
for (int s = 0; s <= e; s++)
{
LL sum = 0;
for (int i = s; i <= e; i++)
sum += a[i];
maxx = max(maxx, sum);
}
printf("%lld", maxx);
}
void t2()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++) //前缀和从1开始存
scanf("%d", &a[i]), b[i] = b[i - 1] + a[i];
for (int e = 1; e <= n; e++)
for (int s = 1; s <= e; s++)
maxx = max(maxx, b[e] - b[s - 1]);
printf("%lld", maxx);
}
int main()
{
// t1(); //纯暴力
t2(); //前缀和优化
return 0;
}
/*
6
-2 11 -4 13 -5 -2
*/ 2-最大子段和-递归
分析论
(1)算法思想
A.部署find(k)函数,用于寻找到【必定选中第k个元素的最大子段和】
部署备忘录m[k],来记录find(k)的数值,如果递归过程发现find(k)执行过一次了,就从备忘录里面调动(直接return m[k])(int型函数提前return就算终止掉了不会再往下运行)
B.递归边界:k=0时候,说明递归探底(因为我们数据从a[0]开始存储)
这时候返回a[0],同时部署m[0]
C.递归划分:思想论·当前选中第k个元素的最佳状态是和之前形成的最大字段和有关的,考虑两种状态
a.选择前面的最大子段和,并且把k号元素加上(衔接过程)
b.不选择前面的最大子段和,重新从当前第k号元素开始(另立门户)
b选项的递归决定了起点的选择,a选项则决定了子段和的长度在哪里
前面最大子段和:find(k-1)
当前k号元素:a[k]
那么我们m[k]=find(k)=max(a[k],a[k]+find[k-1]);
阶段结束后要存储到m[k]中并return
D.最后扫描一遍备忘录m,把max弄出来
E.关于先进书写的补充:return a=b;会先赋值后返回
相当于把【内部语句】拆分到上一行,执行完成后再return
F.关于时间复杂度:这是带着备忘录的递归,只会从n探底到0 1次,其他时间会通过备忘录调取,不会再执行find函数
代码区
#include
#include
#include
using namespace std;
const int N = 1e5 + 7;
int a[N], n, m[N], maxx = -2e9;
//带备忘录的递归,时间复杂度降低到O(N);是最先进的书写
int find(int k) //当前第k个元素可以形成的最大
{
if (m[k] != 0) //主要是回溯的时候避免重复计算,降低时间复杂度
return m[k];
if (k == 0) //递归探底,返回第一个元素(以第一个元素为起点)
return m[0] = a[0]; //首发元素部署
m[k] = max(a[k], find(k - 1) + a[k]);
//只要当前元素(新建起点) 或 前缀max(某个起点)+当前元素
//到0就return了,不会再向下找
return m[k];
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i++)
scanf("%d", &a[i]);
find(n); //递归探底
// m[k]:以第k个元素结尾,所能形成的 max前缀和
//(起点在下层递归中自适应形成)
for (int i = 0; i < n; i++)
maxx = max(maxx, m[i]);
printf("%d\n", maxx); //把max扫出来
return 0;
}
/*
6
-2 11 -4 13 -5 -2
6
-2 1 -4 -13 -5 -2
如果全是负数的话,就是扫描一个最大的数值出来
*/
2-最大子段和-分治
分析论
(1)算法思想
A.部署find(l,r),意图返回区间l~r之间的最大公共子序列
递归边界在l=r时候,说明只有一个元素,那返回a[l] a[r]都可以
B.三分法思想·论当前最大公共子序列可能出现的位置
a.左侧区域 find(l,mid)
b.右侧区域 find(mid+1,r)
c.中间区域
以mid为切分,向左取得最长字段sum,向右同样取得sum
二者sum求和就是中间区域的最大子段和
(向左向右限制都不得超过当前lr范围)
以上为子状态分治拆分的结果,当前结果只能是以上三者之一
以上三个取得一个max就是当前l~r之间的最大公共子序列
关于时间复杂度
a. 单次求和复杂度O(1)
b. T(n)=2*T(n/2)+O(n)
两个是左右开递归的时间复杂度,n是中间部分的时间复杂度
c. 求解就是nlogn
代码区
//【最大子段问题】·分治算法P58
#include
#include
using namespace std;
const int N = 1e5 + 7, inf = -2e9;
int a[N], n;
int get_maxM(int l, int r)
{
int mid = l + r >> 1;
int ML = inf, MR = inf, sum = 0;
for (int i = mid; i >= l; i--) //中区左半部分最大值
{
sum += a[i];
if (ML < sum)
ML = sum; // Max_L
}
sum = 0; //恢复一下
for (int i = mid + 1; i <= r; i++) //中区右半部分最大值
{
sum += a[i];
if (MR < sum)
MR = sum; // Max_R
}
return ML + MR; //得出中区的max
}
int ans(int &a, int &b, int &c) //返回三个中的最大值
{
a = max(a, b);
a = max(a, c);
return a;
}
int find(int l, int r)
{
// printf("%d %d\n", l, r);
if (l == r) //只有一个元素,无法切分的情况
return a[l];
int mid = l + r >> 1;
int maxL = find(l, mid); //【左半区】递归
int maxR = find(mid + 1, r); //【右半区】递归
int maxM = get_maxM(l, r); //【中区】终章返回
return ans(maxL, maxR, maxM); //返回三者的最大值
}
int main()
{
scanf("%d", &n);
for (int l = 0; l < n; l++)
scanf("%d", &a[l]);
printf("%d", find(0, n - 1));
return 0;
}
/*
最大子段有三种出现情况
1.全在左半区 maxL
2.全在右半区 maxR
3.踩在mid上 从中间向两侧延伸的max
*/
/*
7
-2 -11 -4 -13 -1 -2 -5
6
-2 -11 14 -13 -5 -1
*/ 2-最大子段和 - 一维度DP
分析论
A.DP[k]:包含第k个元素的子段,最大和是多少
B.子状态分析:
a.前端衔接:a[k]+dp[k-1]
b.前端抛弃:a[k]
这个和上边的递归思想是一脉相承的
b方案就是舍弃前面的另立门户,a方案就是衔接前面的
二者取得max即可
C.注意事项:由于涉及到d[i-1]状态,所以数组从a[1]开始存储
代码区
#include
#include
#include
using namespace std;
const int N = 1e5 + 7;
int n, a[N];
int dp[N]; // dp[k]:包括a[k]在内,最长子段和是多少
/*
由两种子状态转移来
dp[k-1]+a[k]
a[k]
两个取max来
*/
void show()
{
for (int i = 1; i <= n; i++)
printf("%d ", dp[i]);
puts("");
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]);
int sum = -2e9;
for (int i = 1; i <= n; i++)
{
dp[i] = max(dp[i - 1] + a[i], a[i]);
sum = max(sum, dp[i]);
}
//show();
printf("%d", sum);
return 0;
}
/*
6
-2 11 -4 13 -5 -2
*/ 2-最大子段和 - 零维度DP
分析论
A.我们观察到当前dp[i]和dp[i-1]有关,到达第i次循环时候
B.认为当前dp就是dp[i],而dp在没有【更新】之前是dp[i-1]
C.根本就用不到数组dp,只要零维度dp即可
代码区
#include
#include
#include
using namespace std;
const int N = 1e5 + 7;
int n, a[N];
int dp;
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]);
int sum = -2e9;
for (int i = 1; i <= n; i++)
{
dp = max(dp + a[i], a[i]);
sum = max(sum, dp);
}
//内层的dp相当于dp[i-1]
//我们最新外层更新的dp相当于dp[i]
// show();
printf("%d", sum);
return 0;
}
/*
6
-2 11 -4 13 -5 -2
*/ 3-01背包-二维
分析论
1.宏观部署
F[i][y]:DP数组,属性为【最大价值】,表示只考虑前i个物品时,总重量不超过y的前提下,可以取得的最大价值是多少
N、m:n个物品,背包最多承重为m
W v:weight物品重量,value物品价值
2.状态表示
当前状态由前方状态承接而来,
A.选择第i个物品:
B.不选择第i个物品:
以上为两个子状态,我们最终要输出f[n][m]状态
(考虑前n个物品,总重量不超过n的最大价值)
3.状态转移方程
T1.如果装得下:
需要考虑选择和不选择,哪种价值会最大化?
A.选择,那就从【考虑前i-1个物品】【减去物品i的重量】的状态转移过来,价值是在上
一个状态的基础上+v(当前第i个物品的价值):F[i][j]=f[i-1][j-w] + v
B.不选择,那就直接延承f[i-1][j]
以上两种方案需要进行比较,选择最大价值写入
T2.如果装不下:
那就不选择第i个物品,当前状态就直接延承考虑前i-1个物品
体积不超过j的状态:f[i][j] = f[i-1][j]
4.具体实践
需要关注一个问题,在考虑第i个物品时候,当前背包能不能装得下
三目运算符,会先让内部max执行之后再赋值
代码区
#include
#include
#include
#include
using namespace std;
const int N = 1e3 + 7;
int n, m, w, v, f[N][N]; //考虑前i个物品,容量不超过j的最大价值
// f[x][y]:考虑前x件物品中,当前使用的体积不超过y时,所能取得的最大价值
/*
状态转移方程、
1.不选择:f[x][y]=f[x-1][y] 直接不考虑第x个物品,体积不变
2.选择:f[x][y]=f[x-1][y-w[x]]+v[x] 减去第x个物品的体积,加上价值
默认不选择,如果体积OK考虑选择,二者取一个max
最终结果在f[x][0-v]中取出max即可
*/
int main()
{
scanf("%d%d", &n, &m); //物品个数+背包大小
for (int i = 1; i <= n; i++) //寻访,每一件物品
{
scanf("%d%d", &w, &v); //重量+价格
for (int j = 0; j <= m; j++) //寻访,每一寸体积
f[i][j] = j < w ? f[i - 1][j] : max(f[i - 1][j], f[i - 1][j - w] + v);
}//如果背包够装,就取max;装不下就只能延承i-1不添加新物
printf("%d", f[n][m]);
return 0;
}
/*
01背包
物品只能选一次,选或者不选
选只能整个选
思想·苏晓辉のDP思想(建议多做题?)首发思考二维
0.状态表示:【前i个物品】【某种限制】(如体积等)
坐标表示什么集合?
考虑前i个物品,总体积不超过j;的方案的最大值 集合
存的数值和集合之间是什么关系?
方案集合中的最大价值
1.状态计算 固定套路,【看最后一个或几个物品的不同点】
f[i][j]的子集划分(子集首先要满足f[i][j]限制)
(子集通过某种变化,可以转移为当前的状态)
A.选择第i个物品后体积=j:f[i-1][j-w[i]]+v[i]
(前i-1个物品中,总体积小于j-w[i]的最大价值,再加上选中第i个物品)
减去重量,获得价值。
B.不选择第i个物品体积=j:f[i-1][j]
(只考虑前i-1个物品,总体积小于等于j)
二者取max(B方案启用需要判断,背包体积是否能容下)
默认选择第一方案
大致一个感知:前面随便选,最后考虑是否包含物品i即可
在递推过程中每一步都取得最优解,子问题也拿到最优解
最终得出全局的最优解
3.时空优化 看递推公式
发现只需要用到上一层的情况
所以二维降维一维
4.优化控制
从大到小,防止出现“串联”
j在右侧侧j-w在左侧;更新点是右侧的j
从大到小递推,可以保障j-w都是上层i-1的数字
从小到大递推,你访问的j-w可能是前几轮更新已经更新过的变成了第i层而非i-1层
DP优化过程要保证前后代码等价
*/
/*
01背包:每个物品最多只取得一次
完全背包:每个物品可以取得无限次
多重背包:每个物品最多取得Si个(每个物品有多个副本)
优化问题:
分组背包问题:多分组每组有若干物品,每组里边只能选1个
*/ 3-01背包-一维
分析论
5.维度压缩(优化)
A.思想来源:
我们发现f[i][j]只与f[i-1][j]上一层有关,我们在进入下一层循环的时候,在算法执行之前f中存储的就是上一层i-1的数据,我们新算出来的f[i]覆盖进去就可以了
B.改造思路 对f的意义进行优化定义,压缩成一维度
F[x]:体积不超过x时的最大价值
C.注意事项 为什么是从大到小枚举?
简单来说,因为我们【当前状态】的生成需要使用到【之前状态】,会调动f[i-v],如果我们从小到大进行枚举,f[小数字]会被率先更新为【当前状态】(覆盖掉了),那么我们算到f[大数字]时候需要调动f[小数字],但是此时的f[小数字]已经不是【之前状态】了,出现异常覆盖!
为了确保 f[j-v[i]]这个状态没有更新过,是i-1层的
而不是出现用本层更新过的数据,认为是上一层的数据来参与计算
出现 “串联”;所以让j从大到小枚举
j在右边,j-v[i]在左边;一路向左推过去,只是更新最右侧的j
即可确保右侧更新是进行比较的【左端点】是来自i-1层
思想上,如果认为序列n很长,我们从左向右推进
更新右端点,采用的【左端点】,必然会遇到第i层(本轮)已经更新过的右端点,这就不对了
D.优化论
从大到小枚举从【最大体积】枚举到【当前物品体积】即可,可保障当前背包容积一定能够装下当前物品,就不要再去搞三目什么的了
E.状态转移论
F[j]相当于f[i][j],只要考虑f[i-1][j]和f[i-1][j-w]+v的情况即可,取max
二维压缩的话把第一维度的i去掉就可以了,新覆盖进去的就相当于i
里面存储的相当于i-1层
代码区
#include
#include
#include
#include
using namespace std;
const int N = 1007;
int n, m;
int f[N];
/*
二维改进,发现当前层状态只和上一层有关
那么可以压缩为一层即可
f[x]:所有体积小于等于x的方案,取得的最大价值
*/
int main()
{
scanf("%d%d", &n, &m); // n个物品,m的背包体积
for (int i = 1; i <= n; i++)
{
int v, w; // v是价值,w是体积
scanf("%d%d", &v, &w);
for (int j = m; j >= v; j--) //从全体积开始考虑,以装的下为标准
f[j] = max(f[j], f[j - v] + w);
//【至少能装得下1个】,才考虑要不要更新
//否则就是【延承】i-1位置的数据
} /*
为什么是从大到小枚举?
为了确保 f[j-v[i]]这个状态没有更新过,是i-1层的
而不是出现用本层更新过的数据,认为是上一层的数据来参与计算,出现 “串联”
所以让j从大到小枚举
j在右边,j-v[i]在左边;一路向左推过去,只是更新最右侧的j
即可确保右侧更新是进行比较的【左端点】是来自i-1层
思想上,如果认为序列n很长,我们从左向右推进
更新右端点,采用的【左端点】,必然会遇到第i层(本轮)已经更新过的右端点
这就不对了*/
printf("%d", f[m]);
return 0;
} 4-独立任务最优调度 - 二维
分析论
1.问题论述
有两台机器AB,需要批改n个作业,每个作业给不同的机器所需要的批改时间是不一样
的,分别记作a[x] b[x];现在给出这一组作业,输出两台机器完成批改所需的最短时间。
2.状态表示
A.集合表示
F[x][y]:处理完前x作业,A机器总用时为y时,B机器最低用时
B.集合属性
取得min(B机器最低用时),分别用两个for循环进行状态更新,第一层遍历所有作
业,第二层遍历A所有可能的时间状态
C.额外说明
a)关于A机用时状态
由于第二维度需要遍历A机器所有可能的时间状态,所以我们在全局变量部署一个
time_A,作为所有作业都给A批改时的A机总用时
b)关于真实用时
最终完成批改的时候,A机器和B机器各自耗时或为不同,需要取得二者最大
值为所有任务完成用时
3.状态转移
状态论:我们认为前i-1个作业全部批改完成,现在第i个作业给谁?
A.给A机器:那么B机器时间不变(F直接延承)从哪里延承?
思考认为,此时(处理完成第i个作业)和(第i个作业还没处理) 时候的B机器用时是
【一致的】,也就是:F[i][j]=f[i-1][j-a[i]]
(A机器减去第i个作业用时·前状态)
(【A机尚未处理第i个作业时的机器B用时】=【A机处理完成第i个作业时的机器B用时】)
B.给B机器:那么B机器需要加上(处理第i个作业所需用时)
思考认为,此时A机用时是不变的(第二维度j不变),也就是
F[i]][j]=f[i-1][j]+b[i]
(B处理前i-1个作业用时)+(B处理第I个作业用时)
4.注意事项·朴素
数组地址不能是负数,需要注意当前作业给A机器用时,如果超过A机器总用时j时候,A机器是没法处理这个作业的,只得交由B机器处理。
否则就是AB状态都计算一下,取得min来更新f[x][y]
全部处理完成时候,真实时间需要另外写一个for循环,枚举AB机器在阶段状态的用时,取得max真实时间之后,得出全局最小真实时间
5.时间复杂度
两层循环O(n^2),实际上会比n²大一点,因为第二维度遍历的是A机器全部时间状态,通常情况下比n大
代码区
//独立任务最优调度问题
#include
#include
#include
#include
using namespace std;
const int N = 1e4 + 7;
int a[N], b[N], f[N][N];
int A_all, n, min_t = 0x3f3f3f;
int dp()
{
for (int i = 1; i <= n; i++) //遍历,所有作业
for (int j = 0; j <= A_all; j++) //遍历,A机所有时间
{
int ta = f[i - 1][j - a[i]];
int tb = f[i - 1][j] + b[i];
//交由A机处理时候,B机延承(A尚未处理第i个作业)时的B机用时
//交由B机处理的时,A机用时不变,B机用时+处理第i个作业的用时
//第i个作业耗时在A机(当前最大耗时)的承受范围之内,取得min
//否则只得交由B机处理
f[i][j] = a[i] > j ? tb : min(ta, tb);
}
for (int i = 0; i <= A_all; i++) //扫一遍,A所有可能的时间
{
int t = max(f[n][i], i);
// A机用时为i,此时B机用时为f,二者取max是实际完成的用时
if (min_t > t) //意图取得min
min_t = t;
}
return min_t;
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
scanf("%d", &a[i]), A_all += a[i];
for (int i = 1; i <= n; ++i)
scanf("%d", &b[i]);
printf("%d\n", dp());
return 0;
}
/*
6
2 5 7 10 5 2
3 8 4 11 3 4
*/
/*
状态表示
集合:f[i][j]全局总用时:处理完成前i个作业,A机器总用时为J时,机器B的最低用时
属性:min I:第I个作业 J:A总用时 内存:B用时
真实用时t=max(j,f[n][j]);//处理完成n个作业,.
状态计算
子集分析:边界情况,认为i-1个作业处置完毕,看第i个作业给谁处理
A.给A机器处理:f[i][j]=f[i-1][j-a[i]],B机器用时没变
A机处理第i个作业前,B机用时;不变!
B.给B机器处理:f[i][j]=f[i-1][j]+b[i]
(B处理前i-1个作业用时)+(B处理第I个作业用时)
(A机没有新任务,时间不变)
注意一个边界,循环J时候,如果J=a[i])
那么第I个作业只能给到B机器处理
否则就AB中取得min进行转移
状态转移:
状态不合法:由B转移得来, 否则:AB中取得min进行转移
f[i-1][j-a[i]]:第I作业给到A处理,B机器总用时不变,延承
f[i-1][j]+b[i]:第I作业给到B处理,A机器总用时不变,加上B处理第I作业的情况
初始化:部署0即可,没开始处理都不耗时
*/ 4-独立任务最优调度 - 一维
分析论
7.压缩优化
A.观察发现
当前f[i][j]和上一层的f[i-1][j]是有关的,不涉及跨层,那么就可以用类似于01背包优化的办
法给他第一维度搞掉;我们当前计算得出的就是当前的f[i][j],在计算开始前f里面存的就
是i-1层的内容
B.进化思想
F[x]:A机器用时最大为x时候,B机器的最低用时
8.进化优势
A.节省了不必要的空间,实现了空间优化(时间复杂度不变)
B.能够处理更大规模的问题
如果是二维f,N最多=1e4+7,再多就爆堆栈了
现在一维度f,N最多=1e7+7,可以处理更多更复杂的状态
9.注意事项·进化
和01背包一样,因为这里需要调用【上层f[小数字]状态】,所以部署为从大到小扫
描,避免出现错误覆盖,导致对【非上层状态】的引用,导致错误结果。
类似于01背包的思想,为什么我们这里j不是限制到a[i]来确保这个任务是可以交由A
机器处理的呢?
因为这违背了转换等价性原则。
在a[i]>j的部分,我们原则上是要部署tb=f[i-1][j]+b[i]的
如果把这部分不进行计算(就是限制最小到a[i]) 那么我们实际上是部署了tb=f[i-1][j]
01背包之所以能进行限制,是因为他不限制的时候,状态方程刚好是上边这个
我们这个问题时要把b[i]给加上。
代码区
//独立任务最优调度问题
#include
#include
#include
#include
using namespace std;
const int N = 1e7 + 7;
int a[N], b[N], f[N];
int A_all, n, min_t = 0x3f3f3f;
int dp()
{
for (int i = 1; i <= n; i++) //每个作业
for (int j = A_all; j >= 0; j--) // A机器所有时间状态
{
int ta = f[j - a[i]];
int tb = f[j] + b[i];
f[j] = a[i] > j ? tb : min(ta, tb);
}
for (int i = 0; i <= A_all; i++) //扫描,处理完成N个作业时候,
{
int t = max(f[i], i); // A B机器中最大耗时为真实时间
if (min_t > t) //取得真实时间的最小值
min_t = t;
}
return min_t;
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
scanf("%d", &a[i]), A_all += a[i];
for (int i = 1; i <= n; ++i)
scanf("%d", &b[i]);
printf("%d\n", dp());
return 0;
}
/*
6
2 5 7 10 5 2
3 8 4 11 3 4
*/
/*
状态表示
集合:f[i][j]:处理完成前i个作业,A机器总用时为J时,机器B的最低用时
属性:min I:第I个作业 J:A总用时 内存:B用时
真实用时t=max(j,f[n][j]);//处理完成n个作业,.
状态计算
子集分析:边界情况,认为i-1个作业处置完毕,看第i个作业给谁处理
A.给A机器处理:f[i][j]=f[i-1][j-a[i]],B机器用时没变
(【A机尚未处理第i个作业时的机器B用时】=【A机处理完成第i个作业时的机器B用时】)
B.给B机器处理:f[i][j]=f[i-1][j]+b[i]
(B处理前i-1个作业用时)+(B处理第I个作业用时)
(A机没有新任务,时间不变)
注意一个边界,循环J时候,如果J=a[i])
那么第I个作业只能给到B机器处理
否则就AB中取得min进行转移
状态转移:
状态不合法:由B转移得来, 否则:AB中取得min进行转移
f[i-1][j-a[i]]:第I作业给到A处理,B机器总用时不变,延承
f[i-1][j]+b[i]:第I作业给到B处理,A机器总用时不变,加上B处理第I作业的情况
初始化:部署0即可,没开始处理都不耗时
*/ 5-哈夫曼编码(线段树结构)
极光 · 哈夫曼树の生成(非指针实现 仿邻接表)_影月丶暮风的博客-CSDN博客
分析论
没啥好分析的,每次选两个权最小的结点,提出来就是了
这里采用的是线段树结构,因为node*在【结构体排序】【结点的保存】上遇到了难以逾越的问题
被迫采用线段树
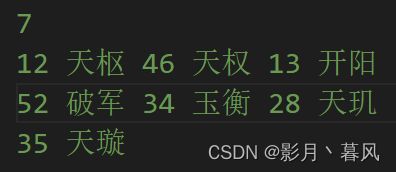
本题测试数据-璃月七星北斗七星
线段树数据实例
举几个例子:
8号点,L=1说明左节点是【天枢星12】R=3说明右节点是【开阳星13】
10号点,L=5【玉衡星34】 R=7【天璇星35】,W=98是二者权值之和。
本身结点为【生成结点】,W=25说明权值=25
我们测试数据只有7个数据,在1~7的数据我们视作【叶子结点】,其余的视作
【生成结点】,在优先队列生成过程中,非叶子结点会被指向name[idx=0]。
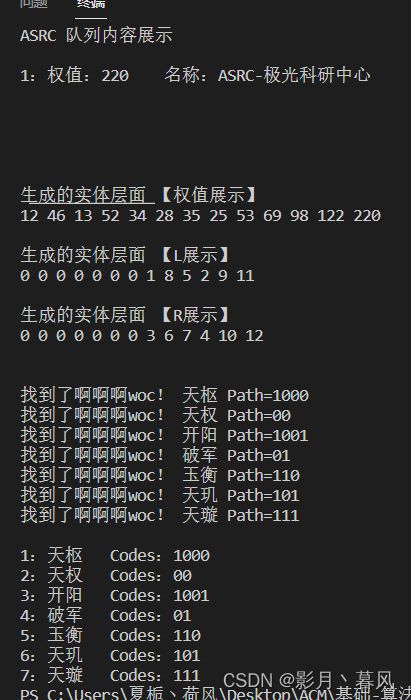
关于find的论述
就是线段树DPS过程,我们递归边界是看way(实体结点坐标idx)是否小于等于n(从1启存,叶子结点范围是1~n)是否落在1~n范围,这说明我们已经探测到了叶子结点。
此时我们将递归携带的destination字符串数组和对应叶子结点的name[i]进行比较,如果相同说明就找到了这个叶子结点。
边界终止判断之后,就是对左叶子结点,右叶子结点的递归探索过程,其中左右结点坐标来自LR数组。
关于在find函数中用到的几个数据进行说明
path[i]:路径数组,向左记作false,向右记作true,在向下递归开始前进行部署
Codes_idx:当前正在寻找的目标叶子结点,在线段树中的下标
Des[]:char数组,正在寻找的结点名称
Code[i]:string数组,存对应结点的哈夫曼编码的
Step:记录当前走了几步,来对path进行寻访,生成路径存入code
Way:当前结点在线段树中的idx下标
关于边界情况的论述
触发边界条件的时候,对应的path[step]没有生成,而step-1的path全部生成完成
代码区
// ASRC-极光科研中心 哈夫曼编码 - 非指针实现
// 思想参考AcWing图论中,对于【邻接表】的运用
// 因为【结构体优先队列】似乎无法对【node*】的排序
// 暂时无法突破这个技术难点,只能退而求其次
// 不过调整后的实际运用效果还是不错的
// 2022-06-22 鸿蒙纪元·乾坤 Day294
// 这里就是LR改成int,用idx作为指针
// 优势在于规避了 node *l,*r 的出现,可以实现同样效果
// 缺点在于需要预定义内存,不能实现动态内存和释放
// 从我实践的角度出发,算法竞赛中是以实现为目的,不要太追求这种细枝末节
// 以后的工程实践过程中再考虑这种产品优化的问题吧
#include
#include
#include
#include
#include
using namespace std;
#define top hfm.top()
#define pop hfm.pop()
#define size hfm.size()
#define push(x) hfm.push(x)
//【数据存储模块】
const int N = 1e5 + 7, T = 2 * N - 1;
struct node
{
int w; //权重
int idx; //结点name下标,=0时候表示是生成结点
int st; //实体idx,记录【结点】在【线段表】位置
//【线段表】:wlr三剑客
};
bool operator<(node t1, node t2)
{
return t1.w > t2.w; //新插入T2更小,意图构造大头
//实际上恰好相反
}
int n; //【初始结点个数】
int idx = 1; //【新结点存储位置】仿造邻接表
int HFM; //【哈夫曼树根节点idx】
bool path[N]; //【搜索路径】
string codes[N]; //【结点对应的哈夫曼编码】
int codes_idx; //【哈夫曼编码追踪标记】:当前捕获的path对应哪个结点
int l[T], r[T], w[T]; //【左节点idx】【右节点idx】【结点权值】
priority_queue hfm; //【生成树辅助优先队列】,存储结点对应的idx下标和权值,权值小的往前排
char name[N][27] = {"ASRC-极光科研中心"}; //【结点名称】,
//【测试函数模块】
void show_queue()
{
puts("\n\nASRC 队列内容展示\n");
int tmp = 0;
while (size)
{
printf("%d:权值:%d", ++tmp, top.w);
printf("\t名称:%s\n", name[top.idx]), pop;
}
puts("\n\n");
}
void show_node()
{
puts("\n\n生成的实体层面 【权值展示】");
for (int i = 1; i <= HFM; i++)
printf("%d ", w[i]);
puts("\n\n生成的实体层面 【L展示】");
for (int i = 1; i <= HFM; i++)
printf("%d ", l[i]);
puts("\n\n生成的实体层面 【R展示】");
for (int i = 1; i <= HFM; i++)
printf("%d ", r[i]);
puts("\n\n");
}
//【功能函数模块】
void get_in()
{
scanf("%d", &n);
for (idx = 1; idx <= n; idx++)
{ //跳出的时候,idx指向n+1
scanf("%d%s", &w[idx], &name[idx]);
node tmp = {w[idx], idx, idx};
//第一个idx,结点名称位置,也代表是不是合成结点
//第二个idx,作为一个结点,在实体层面的下标(w中的下标)
push(tmp);
}
}
void c_Tree()
{
while (size != 1)
{
node t1, t2, t3;
t1 = top, pop;
t2 = top, pop;
{ //新建结点(实体层面)
t3.w = w[idx] = t1.w + t2.w;
t3.idx = 0; //表示是【合成结点】
t3.st = idx; //实体层面坐标
l[idx] = t1.st;
r[idx] = t2.st;
}
push(t3); //新建结点(虚空层面)
idx++;
}
HFM = top.st;
}
void find(char des[], int way, int step) // destination
{
if (way <= n) //追踪坐标落到了1~n,说明是叶子结点了
{
if (strcmp(des, name[way]) == 0)
{
printf("找到了啊啊啊woc! %s Path=", des);
for (int i = 0; i < step; i++)
{
printf("%d", path[i] ? 1 : 0);
codes[codes_idx] += path[i] ? '1' : '0';
}
puts("");
}
return;
}
path[step] = false, find(des, l[way], step + 1);
path[step] = true, find(des, r[way], step + 1);
}
void show_code()
{
for (int i = 1; i <= n; i++)
codes_idx = i, find(name[i], HFM, 0); // 0表示已经走了几步
}
void show_remember()
{
puts("");
for (int i = 1; i <= n; i++)
printf("%d:%s Codes:%s\n", i, name[i], codes[i].c_str());
}
//【主战函数模块】
int main()
{
get_in(); //【结点读入】《读入后,第一次展示》
c_Tree(); //【建立哈弗曼树】wlr三剑客,线段表建树
show_queue(); //【展示优先队列】
show_node(); //【调试-wlr三剑客 内容展示】
show_code(); //【展示,各个结点对应的哈弗曼编码】
show_remember(); //【展示,string生成的哈夫曼编码】
return 0;
// show_queue();//【调试-优先队列 内容展示】破坏性读取(全部弹出)
}
/*
7
12 天枢
46 天权
13 开阳
52 破军
34 玉衡
28 天玑
35 天璇
*/ 6-01背包-递归回溯
分析论
代码区
#include
#include
using namespace std;
const int N = 1e5 + 7;
int n, c, v[N], w[N], maxx = -2e9;
void find(int i, int remain, int value)
{
if (i == n)
{
maxx = max(maxx, value);
return;
}
if (remain >= w[i])
find(i + 1, remain - w[i], value + v[i]);
find(i + 1, remain, value);
}
int main()
{
scanf("%d%d", &n, &c);
for (int x = 0; x < n; x++)
scanf("%d%d", &w[x], &v[x]);
find(0, c, 0);
printf("%d\n", maxx);
return 0;
}
/*
物品20个,容量200,重量+价值 454
20 200
24 50 42 60 20 49 7 15 48 115
4 11 3 8 7 5 52 66 50 25
5 8 9 25 14 40 9 22 55 42
40 30 35 49 33 16 12 12 65 127
*/ #include
#include
using namespace std;
const int N = 1e5 + 7;
int n, c, v[N], w[N], maxx = -2e9; //递归流
int work(int x, int c)
{ //第i个物品选择,体积选择
if (x < 0 || c < w[x])
return 0; //全部署完成,或装不下
int a = work(x - 1, c - w[x]) + v[x];
int b = work(x - 1, c);
return max(a, b);
}
int main()
{
scanf("%d%d", &n, &c);
for (int x = 0; x < n; x++)
scanf("%d%d", &w[x], &v[x]);
printf("%d", work(n, c));
return 0;
} 6-01背包-迭代回溯
分析论
1.回溯原理
树形结构,在递归过程中可以得到剪枝(如果当前情况足以判断子树探底往下一定不符合我们最终目标的条件(比如背包放不下了,下面的物品就不考虑了)),每层代表一个元素的一种状态,探底时候是所有元素的1种状态,树状结构的路径相当于对状态的全排列,实现探底也就意味着符合题目的约束条件。
2.01背包的回溯运用
n个物品,每种物品有选和不选2种状态,可以用二叉树结构实现回溯探底,并且根据实时背包容量进行约束剪枝;实现探底的时候我们看一下当前背包取得的价值,用maxx记录是否是最优的方案。
3.迭代回溯
A.宏观设计-探底措施
外层大循环用于遍历每个物品(在过程中i通过stack进行回溯),指针指向i是考虑是否将第i个物品放入背包;如果【情况1:能放入且放入】就放一下,【情况2:放不了且不放入】放不了会自动i+1(跳过这个物品),其实已经蕴含在for循环中(所以就不用在if下再写了)
B.宏观设计-回溯措施
Stack结构部署背包Bag,用于存储【放入背包的元素序号】,回溯的时候弹出最顶上(最后放入的物品),让i=top,在for循环控制下寻访i+1,跳过这个top,因为这个top的情况已经考虑过了,回溯步骤其实就是取出已经放入物品的过程,即【情况3:能放入且不放】,腾出背包空间意图放入其他的物品
弹出措施要注意,不仅仅是访问top,还要pop一下【bug修复报告】另外,弹出的序号用于更新i,在下一轮for会自动+1,跳过这个top;同时vw要做出调整(价值重量把第i个物品取出来(i是top刚弹出来的元素))
C.宏观设计-常规边界
在放置模块结束后,看一下i是否指向n-1(因为我们是从0~n-1存储的),如果是,说明n个物品的放置情况都考虑过了,可以输出一种方案了(不是输出,应该当前获得的总价值v_max是和maxx进行比较,取得max)。
常规边界需要进行回溯1步。
D.宏观设计-极限边界(终止条件 · 重难点)
极限边界情况是需要回溯2步的,这是为什么呢?
先说说何为极限边界,就是背包弹出了最后一个物品i,我们发现i是第n件物品(最后一件物品);倘若此时用【常规边界】进行回溯,我们i++后会取得i=n(我们从0启存,边界到n-1),这时候指针就溢出了。
上面是从指针溢出的角度进行考虑,我们现在从方案的角度进行考虑。回溯2步可以保证方案不会出现重复,为什么这么思考呢
假如7件物品我们放入了237(极限边界),弹出2块可以让i=3(最后弹出的物品),然后在for循环中i++,开始考虑24的情况(以此实现了不重不漏)(抽象的实在太难讲了,我只能举例子,你们思考一下)
假如237按照(常规边界),只弹出1个,i=7,+1后溢出了,查无此元素,就脱离了实际情况。 所以我们需要回退2步,让物品多弹出一个
极限边界如何知道完成遍历了所有的情况?
我们部署的终章情况是(最后元素是n,并且弹出后bag.empty)
还是刚才237的例子,我们在程序中首先【考虑放入】再【考虑不放入】
最后元素=7,弹出后bag.empty说明前面6件物品的放入不放入2种情况都 考虑过了,现在是最终元素考虑不放入的情况,我们从1111走到了0000,也就完成了整个状态树的遍历。
E.基础工程-变量功能说明
W_now:当前背包内物品总重量 v_now:当前背包内物品总价值
Maxx:背包曾经获得的最大价值 bag:背包栈,存放入物品的【序号】
4.递归回溯
A.宏观设计-边界判断
我们存储0~n-1,在递归过程中,到达剪枝判断条件的时候,i还没有考虑部署或者没有部署的情况,而前面i-1元素都部署完成了;所以我们以i==n来判断,此时0~n-1元素全部部署完成,n没有部署(实际上物品编号n不存在),认为完成了一种方案部署,进行价值max的判断
B.宏观设计-回溯措施
探底后会自动return,递归本身就是树形结构,左边return了它会自动往右边走,右边结束了这个节点return再到上一层,上一层再探测右节点.....
我们需要的是控制树形结构的分支,也就是是否选择第i个物品进行分支
如果要放入物品i要看是否能放得下,放入后加上物品的价值和重量
C.宏观设计-背包结构1型 void型
不是引用参数,而是传递参数,所以递归返回后i物品的重量价值就被自动减去了,实现了回溯,不需要额外再去写w-w[i]。Find(a,b,c)意图取得:考虑第i个物品是否放入背包,当前背包容量为remain,当前背包价值为value
向下探索,放入物品i的话,减去重量加上价值,探索i+1;没放的话就直接i+1,不用进行vw的变化
D.宏观设计-背包结构2型 int型
work(x,v)是考虑第完成前0~x-1元素时候,背包容器剩余v时候所能取得的最大价值,由2个子状态转移而来
当前放入:work(x+1,c-w[x])+v[x]
当前抛弃:work(x+1,c)
代码区
#include
#include
#include
#include
using namespace std;
const int N = 1e5 + 7;
int w[N], v[N];
int n, m;
int ans()
{
stack Bag;
int maxx = 0;
int w_now = 0, v_now = 0;
for (int i = 0; i < n; i++)
{
if (w_now + w[i] <= m) //《常规放置-可放入 + 放入》
Bag.push(i), w_now += w[i], v_now += v[i];
//《常规放置-不可放入 + 不放入》
if (i == n - 1) //【边界情况】
{
maxx = max(maxx, v_now);
//边界回溯 《常规放置-可放入 + 不放入》
i = Bag.top(), Bag.pop();
w_now -= w[i], v_now -= v[i];
if (i == n - 1) //【终止情况】
{
if (Bag.empty()) //最后弹出的元素是n,且弹出后空栈
break; //说明全部方案部署完成,弹出
//边界回溯
i = Bag.top(), Bag.pop();
w_now -= w[i], v_now -= v[i];
}
}
}
return maxx;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i++)
scanf("%d%d", &w[i], &v[i]);
printf("%d", ans());
return 0;
}
/*
物品20个,容量200,重量+价值 454
20 200
24 50 42 60 20 49 7 15 48 115
4 11 3 8 7 5 52 66 50 25
5 8 9 25 14 40 9 22 55 42
40 30 35 49 33 16 12 12 65 127
*/ 7-旅行售货商
分析论
1. 何谓【分支限界法】
A.区别于回溯法意图取得【所有满足条件的解】,分支限界法更倾向于取得【一个满足条件的(最优)解】
B.回溯法更像DFS,分支限界法更像【升级过的BFS】(如果是采用优先队列的话,因为优先队列总是弹出局部条件最优的情况,未必是一层一层向下探测,有可能跨层探测或者跳回好几个上层来拓展)
C.分支限界法更吃内存,尤其是优先队列结构,因为它不是逐层扩展的,每个节点都需要保存自己的(层数)(路径);常规队列结构也需要额外记录层数
D.只要节点从queue中pop,非边界情况下必须立即进行拓展,下一层满足条件的结点全部塞入queue
E.其实我个人感觉和BFS差不多,多了一个剪枝步骤,结点要记录floor(层数);优先队列多了一个node的path记录
F.分支限界法相较于回溯法,其最大的优势在于【首次探底即最优解(优先队列)】,而回溯法需要【全部探底后进行比较】,才能得出最优解;尽管在某些极限情况下二者都是指数级别的暴搜,但是分支限界法在某些特别的数据情况下时间复杂度可以压缩到O(n),(一路探底,直接出)
2. 最优解情况、算法选择
旅行售货商,商人从城市1出发遍历所有其他城市后返回城市1,求最短路程。
城市的遍历方式是一种【全排列】,意味着回溯法可以做(但是时间复杂度很高,因为你需要探底所有遍历情况),分支限界法可以做(容易思考,就是回溯法的优化,或可,相当于BFS,但是在某些特殊数据情况下,或可一步到达)
3.数据结构与书写优化 - 主函数概览
G:图,邻接矩阵,默认INF=0x3f3f3f3f为走不通(1e9左右),采用INF覆盖优势在于在两个INF相加时候,不会爆int变成负数
path和cost:最优路径 及其路程花费
Node结构:需要记录path、len(已经走的路程花费)、dep(下一层深度,还没走过)
这里构造函数是参考java的,没想到C++也有,已经由极光科研部收录。
Queue结构:结构体优先队列,结点是node,根据len从小到大排
4.实践论-边界约束模块
优先队列中,头部弹出一个结点。
如果这个结点下一层dep=n,说明这是在倒数第二层的结点,下一步没得走了(从dep~n,只有n-dep+1种选择,就是到城市n;前面1~dep-1的城市已经固定下来了,idx=dep=n时候,固定1~n-1,只有1种选择,那么整条path就确定了)走出后即可(探底+返回城市1)。
边界约束条件触发时候,我们要看看这条路径是不是最优解(废话肯定是),记录临时top的path到全局path,记录cost=【1~n-1点已走路径花费】+【n-1点到n点探底路径花费】+【n点到1点回程路径花费】
边界约束条件在优先队列结构的分支限界法中一旦触发,就是找到了最优解,终止整个算法。
5.实践论-剪枝优化模块
看新弹出的top走过的路程len,如果已经严格大于当前全局最短,直接略过不考虑分支拓展了。
事实上优先队列体系不必要加这句话,因为cost只会被更新1次,更新即终止,其他时候cost=inf,所以写和没写都一样。写出来只是为了体现算法的【模板性】
6.实践论-分支拓展模块
Idx=top.dep,下标是 刚才头部弹出结点的(下一层深度),也就是这次分支拓展的起点(还未到访的城市)。
这里有两个思想误区,放到下面讲。
7.实践论-最优解的捕获(局部/全局)
全局最优解,能走的通,并且当前【总路程花费】<【全局最优路程花费】
局部最优解,生成新节点放入,前提是【新路径局部花费】<【全局最优路程花费】
我后面仔细想了一想,这里好像就已经实现了剪枝了,弹出的top都不会大于cost
8.思想误区1- 拓展时,似乎忽略了一些城市(区分i与way[i])
下一个是遍历了idx~n的城市,1~idx-1的城市不考虑嘛。
Idx=top.dep,idx是刚弹出来top结点的下一层层数(目前尚未确定前往哪个城市) 这个思想误区是没有搞清楚i和way[i]的区别
此处i是,【尚未访问的城市的下标】,真正的是哪个城市是way[i]
确认某个城市可以访问,那就放到way[idx]位置上,实现1~idx路径的固定
9.思想误区2-为什么是交换way[idx] way[i](全排列的形成)
意图更新、确认:way[idx],下一步要到哪个城市?
i是扫描还没有固定的、可以作为下一步(下一步就是下一层idx)访问的城市的下下标(从way[idx~n]中捞一个目标放到idx),找到后swap放过去。后面idx~n的结点都有机会放到idx,而idx从1~n,以此实现全排列。
另外,这里是先把top结点先给到a结点后,对a结点way进行swap
以此下一层for循环进来的way,不会受到上一层swap的影响(因为top.way没动)
10.辅助模块(init show函数)
没啥好讲的,G部署inf,way部署1234567,用于形成全排列;无向图
代码区
#include
#include
#include
#include
#include
using namespace std;
#define top Q.top()
#define pop Q.pop()
#define push(x) Q.push(x)
#define size Q.size()
#define INF 0x3f3f3f3f // inf优势在于,相加=2e9,不会溢出爆炸成负数
const int N = 1e4 + 7;
//【数据结构】
int G[N][N]; //图
int n, m; //【顶点数】【边数】
int path[N]; //最优路径
int cost = INF; //最优路径总长
struct node //【活点】(可拓展点)
{
int way[N]; //路径记录(从1启存)
int len; //路径长度(总长度)
int dep; //下一层深度
node() {} //无参构造
node(int a, int b, int p[]) //有参构造
{
len = a, dep = b;
for (int i = 1; i <= n; i++)
way[i] = p[i];
}
};
bool operator<(node t1, node t2)
{
return t1.len > t2.len;
//结构体优先队列,新来的t2小的排在后面,意图构造大头队列
//事实恰好相反
}
int step; //测试使用,记录走了多少步
//【分支限界BFS】
void work()
{
priority_queue Q;
node a = node(0, 2, path); //祖始结点
//总长度=0,从1号点出发(深度为1),下一层深度=2
push(a);
node t; //临时结点
int idx; //临时深度(下一层的)
while (size) //非空
{
t = top, pop; // len最小的node先弹出来,优先进行拓展
idx = t.dep; // 拓展完成后树的深度
if (t.len >= cost) //【剪枝】,当前结点路径长度已经超过最优解
continue;
if (idx == n) //【探底-边界约束】(完成这一步后走到底部)
{
int w1 = t.way[n - 1]; //倒数第二点
int w2 = t.way[n]; //最终点
int g1 = G[w1][w2]; //【一步】最后一段路,探底
int g2 = G[w2][t.way[1]]; //【一步】探底后,从最终点到回家(1号城市)
int c_new = g1 + g2 + t.len; //【出发+探底+回家】总路程cost_new
if (g1 != INF && g2 != INF && c_new < cost) //能走且更优
{
cost = c_new;
for (int j = 1; j <= n; j++)
path[j] = t.way[j];
}
return; //首次探底,就是最优解,直接终止
}
for (int i = idx; i <= n; i++) //【分支拓展】下一步前往 d~n
{
step++;
//【注意!】这里不是说下一步的城市在d~n中选
//而是说在way[idx]~way[n]中选择
//而通过内部交换(下面的swap)实现的全排列,可以覆盖所有城市访问情况
int f1 = t.way[idx - 1]; //出发点from
int g1 = G[f1][t.way[i]]; //到达下一层所需的路径长度
int nc = t.len + g1; //新路径-总长度
if (nc < cost) //更短的路径,才形成新节点放入
{
a = node(nc, idx + 1, t.way); //新建结点,深度+1,路径是tmp中的
swap(a.way[idx], a.way[i]); //【疑难点】借此形成全排列
//为什么是放在这里呢,拿d和i换?
//因为到这一步,说明【下一步】已经确定是前往【城市way[i]】
//而d作用就像idx,指向【下一步】位置;于是我们要把way[i]拿来放在way[idx]位置
//再idx++
push(a);
}
}
}
}
//【辅助函数】
void init()
{
sizeof(G, 0x3f, sizeof(G)); //不可到达路径赋值为0x3f
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
path[i] = i;
for (int j = 0; j < m; j++)
{
int s, e, w;
scanf("%d%d%d", &s, &e, &w);
G[s][e] = G[e][s] = w;
}
}
void show()
{
printf("\nTravel_Path:");
for (int j = 1; j <= n + 1; j++)
printf("%d ", j == n + 1 ? path[1] : path[j]);
printf("\nMin_Cost:%d\n", cost);
printf("Step=%d\n",step);
}
//【主战函数】
int main()
{
init();
work();
show();
return 0;
}
/* 城市数,道路数;起点-终点-权值25
4 6
1 2 30
1 3 6
1 4 4
2 4 10
2 3 5
3 4 20
*/
/*旅行售货商 为例子
一、与回溯法的区别
1.回溯法意图探底取得所有解
分支限界法,意图最快取得满足条件的一个解即可
2.回溯法本质是DFS,分支限界法本质是BFS
3.分支限界法更吃内存
4.一个活结点一旦拓展,就要展开所有可能的子节点
二、常见形态
1.常规队列型
2.优先队列型
每个地方走一遍,最后回到原点,要求路径最短
*/ 8-最小重量机器
分析论
1.回溯法-思想
机器爆炸了,要修复机器,这里有n个部件,每个部件有m个供应商,上级给你分配的开销是all(不得超过);每个供应商都可以供应各个部件,但是来自不同供应商所需的花费和零件重量是不同的;现在要求你找出选择方案,在不超支的情况下使得总重量最小。
那么对于n个部件,可以构成一个深度为n+1的m叉树(根节点不代表任何部件),每层表示一个零件的供应商来源,每次探底为一次方案。
回溯法是通过递归穷举每种方案,在每次探底时保存全局最优方案(判断一下是否是更优秀的方案)
2.回溯法-实现(非迭代)
部署函数work(k,cost_now,weight_now),含义:当前层数,当前开销,当前重量
Work初始传递数值为 0 0 0 ,因为我们【部件/供应商】都是从0开始存的
【剪枝操作】看一下是不是超支了,超支直接中断掉
【递归边界】层数=n,说明0~n-1(一共n个)全部部署完成,已经形成方案将当前重量抛给【判断函数】
【判断函数】看一下当前重量是否更小,如果更小就把这个供应商部署方案tmp 存下来,更新一下最小重量
From是全局最优的部署方案,tmp是临时使用
3.回溯法-时间复杂度分析
指数级别O(mn),回溯本质上就是暴力枚举,每个部件有m个供应商,n个零件都有m个选择,就变成n个m相乘。
4.分支限界法-思想
有明显的属性需求,就是总重量最小,那么在局部或可形成最优情况(当前已经形成的方案部分花费,按优先队列从小到大排序),我们期待top先弹出的结点能够更快接近最优方案。并且方案情况有明显的树状结构。
部署结构体node表示树中的结点,存储【部署方案】【上一层深度】【当前方案的总开销、总重量】;部署结构体优先队列,按照总重量从小到大排序。全局上部署ans
来存储最佳方案。
5.分支限界法-初始化、数据结构设计
带参数的node构造方法,初始化优先队列时候,我们认为祖始结点是第0层
因为我们的cw都是从0启存,所以1号零件在0的位置。
初始化优先队列是考虑,生成第一层的结点搞进去,结点里面的dep部署0是上一层的结点的层数(根节点第0层)。传入当前结点【开销、重量、深度】,部署部件1的供应商是i+1(因为我们扫描供应商从0开始扫描,题目输出是1~m的供应商)
剪枝操作就是看一下是否超支,超支的结点直接减掉。
6.分支限界法-先进书写
7.分支限界法-宏观设计
队列弹出node到t,在不空的情况下会一直弹出。
【边界约束1】结点边界溢出,直接弃用;这里为什么是部署>=n-1呢,因为我们要求优先队列中部署1~n-1个部件即可,最后一个部件的供应商由for循环给出,得出新节点a(头部弹出临时结点为t)
【边界约束2】在当前新节点a生成的时候,看新节点的dep是否=n-1(新节点的上一层是n-1,那么当前结点是n,已经完成1~n部件的供应商选择了,得出一套方案)。这时候看一下有没有超支,没超支的就直接show出来(优先队列中首次探底就是最优方案)
8.分支限界法-边界约束
结点深度约束(当前节点供应商扫描开始前,外层)
探底边界约束(当前结点供应商正在扫描中,内层),新生成了当前层的结点;
当前层结点的上一层是n-1,说明n个方案都部署完成了,触发边界约束
看一下有没有超支?是否为更优化的方案?满足以上两条件进来。
Res存【全局最小重量】,ans存【最优供应商方案】,这里要特别注意n-1位置
这里a是刚生成的结点,最后一个结点的供应商应当是外层for循环的i+1。因为这时候的way还没有写入,最后一个供应商还没部署到way中。
所以先将0~n-2(前n-1个)扫进去ans,最后一个n-1再特判部署为i-1。
这在常规的结点扩展中也是需要特判的。
9.分支限界法-非边界拓展
当前层新节点a已经生成,看一下没到边界情况,那么我们就要用top中的way部署给新节点的way,最后一个点需要特判。
这里变量有偏移有点弯弯绕绕,要仔细想一想。
我们树结构第0层是虚空,第一层部署第一个零件(存储于0号位置),我们当前所在 层数是a.dep+1,例如dep=3时候,我们位于第四层,此时第4个零件部署完成了, 其中1~3来自top的way,4=i+1;但是我们存储way从0启动存储,所以扫描way 从0~2(
10.分支限界法-时间复杂度分析
看数据的特征性,如果有比较明显的小重量会执行的很快,如果重量都差不多那会执行很慢,时间复杂度在O(mn)~O(n)不等。
11.回溯法与分支限界法的比较
回溯法本质是暴搜,所有方案都探底DFS返回得出后,全部比较一遍才能得出最优解;优点是空间占用会少一点,牺牲时间换空间。
分支限界法是【结点化】思想,每个结点内置自己的【路径】,通过某种【局部最优状态】构建队列,依次弹出进行BFS扩展;优点是每次都能取得【局部最优】,更快地达成【全局最优】,牺牲空间换时间。
代码区-回溯
//最小重量机器
#include
#include
using namespace std;
//【数据结构】
const int N = 1e4 + 7;
int n, m, d; // n个部件,m个商店,总开销不能超过d
int c[N][N], w[N][N]; //花费+价格
int from[N], minn = 2e9 + 7; //各个部件来自哪个供应商,最小重量
int tmp[N];
//【辅助函数】
void init()
{
scanf("%d%d%d", &n, &m, &d);
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
scanf("%d", &c[i][j]);
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
scanf("%d", &w[i][j]);
}
void pd(int t)
{
if (minn > t) //重量更小的就记录下来
{
minn = t;
for (int i = 0; i < n; i++)
from[i] = tmp[i];
}
}
void show()
{
printf("%d\n", minn);
for (int i = 0; i < m; i++)
printf("%d ", from[i] + 1);
}
//【主战函数】
void work(int k, int cost_now, int weight_now)
{
if (cost_now > d) //【剪枝】超出经费开支的搞掉
return;
if (k == n) //【探底】遍历完成,并且开支结余
{
pd(weight_now); //判断一下,重量是否更小
return;
}
for (int i = 0; i < m; i++)//【拓展】
{
//扫描每一个供应商
tmp[k] = i; //第k个元素供应商来自i
work(k + 1, cost_now + c[k][i], weight_now + w[k][i]);
}
}
int main()
{
init();
work(0, 0, 0); //部署第0个部件的供应商,当前花费为0,总重量为0
show();
return 0;
}
/*
3 3 4
1 2 3
3 2 1
2 2 2
1 2 3
3 2 1
2 2 2
*/
代码区-分支限界
#include
#include
#include
#include
#include
using namespace std;
//【先进书写】
#define pop Q.pop()
#define push(x) Q.push(x)
#define top Q.top()
#define size Q.size()
//【数据结构】
const int inf = 0x3f3f3f3f;
const int N = 1e4 + 7;
int n, m, all; //零件数量,供货商数量,总预算
int ans[N]; //答案(各个零件选择的供货商)
int c[N][N]; //价格
int w[N][N]; //重量
int res = inf; //最小重量
//不超过总预算前提下,要求总重量最小
struct node
{
int w, c, dep, way[N];
//方案总重量,方案总开销,结点深度(0~n-1),方案内容
node(int a, int b, int c1)
{
w = a, c = b, dep = c1;
}
};
bool operator<(node t1, node t2)
{
if (t1.w != t2.w) //重量低
return t1.w > t2.w;
else //深度浅
return t1.dep > t2.dep;
//新来的更小,意图构造大头,事实恰好相反
}
priority_queue Q;
//【辅助函数】
void init()
{
scanf("%d%d%d", &n, &m, &all);
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
scanf("%d", &c[i][j]);
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
scanf("%d", &w[i][j]);
//开销读入,重量读入
for (int i = 0; i < m; i++) //扫描供应商
{
node t = node(w[0][i], c[0][i], 0); //重量,开销,深度(上一层)
if (t.c > all) //开销超支的,剪枝
continue;
t.way[0] = i + 1;
push(t);
}
// 零件 の 开销,重量都是0~n-1 , dep=0结点,说明0号零件部署完成
// 上层是n-1,说明当前部署到了第n层,需要弹出了
}
void show()
{
printf("%d\n", res);
for (int i = 0; i < n; i++)
printf("%d ", ans[i]);
}
//【主战函数】
void work()
{
while (size)
{
node t = top; //弹出top
pop;
if (t.dep >= n - 1) //深度溢出
continue;
for (int i = 0; i < m; i++)
{
int now = t.dep + 1;
int t1 = t.w + w[now][i]; //重量假设
int t2 = t.c + c[now][i]; //开销假设
node a = node(t1, t2, now); //重量,开销,当前深度
if (a.dep == n - 1) //【探底-当前深度达到n-1】
{
if (a.w >= res || a.c > all) //超支,或新方案没有减少重量
continue; //没寄掉说明方案更好
res = a.w;
for (int i = 0; i < n - 1; i++)
ans[i] = t.way[i]; //记录一下,(前面的n-1个方案)
ans[n - 1] = i + 1; //最后一个特判,因为a是刚生成的node
//它的供应商取决于外层for循环的i(供应商枚举)
return;
} //首次探底就是最优值返回
if (a.dep < n - 1) //【结点拓展】
{
if (a.c > all) //超支剪枝
continue;
for (int i = 0; i < a.dep; i++) //历史路径
a.way[i] = t.way[i]; //内部i,用完销毁
a.way[a.dep] = i + 1; //最后一个特判,因为a是new node
push(a); //塞入
}
}
}
}
int main()
{
init();
work();
show();
return 0;
}
/*
3 3 4
1 2 3
3 2 1
2 2 2
1 2 3
3 2 1
2 2 2
*/