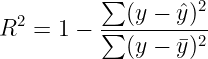基于lingo的线性回归和非线性回归

线性回归和非线性回归的lingo编程实现

目录

1.介绍

1.1 使用工具

1.2 lingo求解回归方程的特点

2.回归方程的求解

2.1线性回归

2.2非线性回归

3.模型推广

---

1.介绍

本文通过建立目标规划的方法求解回归方程。lingo通过目标规划求解线性和非线性回归方程简单有效，容易理解，编程简单。

1.1 使用工具

lingo18

1.2 lingo求解回归方程的特点

        lingo作为一款求解线性和非线性方程方程组功能非常强大的软件，是求解优化模型的最佳选择。很多情况一个问题不止有一个解法。我们在这篇文章中介绍回归方程的另外一种解法。我们求解回归方程通常使用最小二乘法，最小二乘法可以通过以下三种方法求得回归方程参数

1、多元函数求最值（也有的说法把这当成最小二乘法）
2、利用线代的几何意义
3、梯度下降法

求得回归方程中未知参数后得到误差最小的回归方程。

        但是这些方法的步骤较为繁琐，我们考虑到是否可以通过执果索因的方法求解回归方程参数，具体来说就是通过求解误差最小得到回归方程参数。正常来说，这种违背由因得果的方法基本不可能实现，但是我们考虑将其转化为目标规划，以误差最小为目标函数利用lingo求解，得到误差最小时回归系数的最优解，这一方法省去了大量繁琐的步骤。以下将举线性和非线性回归通过lingo目标规划求解的两个例子。

2.回归方程的求解

以下的为原数据，为的平均值，为回归的值。为点的数量。为回归方程参数。

2.1线性回归

        对于一般线性回归 , 我们引入相关系数作为评价指标，越接近于1，吻合程度越高，越接近0，则吻合程度越低。于是我们将作为目标函数求解最大值得到系数最优解。

目标函数：

约束条件：

lingo程序:

model:
sets:
data/1..21/:x,y,y_fit;!创建x,y,x_fit的原数据和回归矩阵;
endsets
data:
x=13,15,16,21,22,23,25,29,30,31,36,40,42,55,60,62,64,70,72,100,130;!读入x,y数据;
y=11,10,11,12,12,13,13,12,14,16,17,13,14,22,14,21,21,24,17,23,34;
enddata
max=R_square;!目标函数为R^2最大;
R_square=1-@sum(data:((y-y_fit)^2))/@sum(data:((y-y_meanvalue)^2));!计算R^2;
@for(data:y_fit=a*x+b);!线性回归函数;
y_meanvalue=@sum(data:y)/@size(data);!求y的均值;
@free(a);!释放a,b的取值范围;
@free(b);
end

求解结果如下表：

	0.8402766
	0.1795222
	8.208418

由于lingo不方便做图，采用Rstudio做出回归曲线：

 

2.2非线性回归

        针对此例我们假设非线性回归方程  进行回归求解。和线性回归一样，我们采用目标规划，这次我们引入评价指标。数理统计中均方误差是指参数估计值与参数真值之差平方的期望值，记为MSE。MSE是衡量"平均误差"的一种较方便的方法，MSE可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据具有更好的精确度。于是我们将最小作为目标函数求解最小值得到系数最优解。

目标函数：

约束条件：

lingo程序：

model:
sets:
data/1..9/:x,y,y_fit;!创建x,y,x_fit的原数据和回归矩阵;
endsets
data:
x=1.5,4.5,7.5,10.5,13.5,16.5,19.5,22.5,25.5;!读入x,y数据;
y=7,4.8,3.6,3.1,2.7,2.5,2.4,2.3,2.2;
enddata
min=MSE;!目标函数为MSE最小;
MSE=@sum(data:(y_fit-y)^2)/@size(data);!计算MSE;
@for(data:y_fit=a*x+b*@log(x)+c);!回归函数;
@free(a);!释放a,b的取值范围;
@free(b);
end

求解结果如下表：

	0.003873966
	0.08187599
	-2.398902
	7.893306

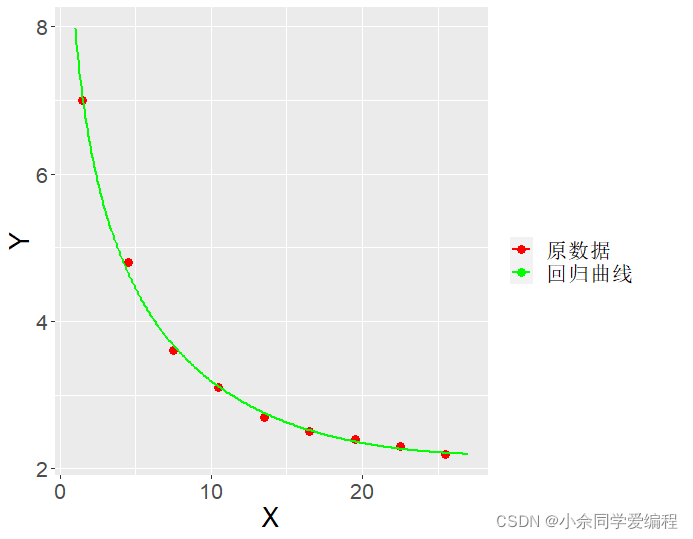
由于lingo不方便做图，采用Rstudio做出回归曲线:

 

3.模型推广

        lingo相比较与其它软件它做回归方程的目标规划求解的灵活性更高。遇到一些特殊情况，在求解回归方程时我们可以通过增加约束方程的形式加入我们的要求。如果使用其它损失评价指标只需改变目标函数和约束条件即可。lingo通过目标规划解决线性和非线性回归方程简单有效，容易理解，编程简单。