【保姆级教程】使用python实现SIR模型（包含数据集的制作与导入及最终结果的可视化）

目录

一、SIR模型介绍

二、Python实现SIR模型

1.制作自己的数据集的两种方法（csv格式）

（1）excel转为csv格式

（2）通过python对csv格式文件进行内容修改

2.导入数据集

（1）具体代码如下所示：

（2）点数据集与连边数据集展示

（3）变量格式展示

 3.制定初始网络

 （1）具体代码如下

（2）重要变量内容格式展示如下

 4. 定义网络节点状态更新规则

（1）具体更新思想

（2）代码呈现如下

5.模拟执行过程并展示结果图

（2）结果图展示部分代码

（3）部分变量内容展示

（4）结果图展示

 三，通过python制作散点图

1.代码部分

 2.散点图呈现

---

一、SIR模型介绍

        经典SIR模型是一种传染病模型，此模型能够简单地展现出一种传染病从出现到扩散再到最后逐渐被消灭的过程。该模型假设总节点数保持不变，且每个个体存在于三种可能的人群状态之中，分别为：S，代表易感人群；I，代表感染人群；R，代表恢复人群（假定恢复人群不会再次被感染）。 三类人群状态之间的转换规则如图1所示：

        SIR模型中除了上述三种人群状态外，还设定了两个常值，分别为感染概率a和恢复概率b。每个时间单位，每个状态为易感人群S的节点若和系统网络中的感染人群I中的节点存在连接，则有a的概率受到感染人群I影响，被感染转换状态，成为感染人群I中的节点。而感染人群I中的节点，在每个单位时间下，则有b的概率，转换自身状态，成为恢复人群R中的节点。

        S(t)，I(t)，R(t)分别代表了当前时间点下，易感人群S总人数，感染人群I总人数及恢复人群R总人数。通过不同人群的占比，我们可以得到当前时刻，感染状态的人群所占总人群的比例，从而了解当前传染病的蔓延程度如何。

---

二、Python实现SIR模型

1.制作自己的数据集的两种方法（csv格式）

（1）excel转为csv格式

将所需数据按列输入excel中

输入完毕后，另存为csv格式进行保存，格式选择如下

 保存完后的csv格式文件在程序中内容如下所示

 

（2）通过python对csv格式文件进行内容修改

具体内容代码参考下方博客即可，写的很详细

通过python编写csv格式文件的四种类型

2.导入数据集

（1）具体代码如下所示：

import pandas
import csv
import random
 
node_df = pandas.read_csv('E:/data/节点.csv')
all_nodes_list = node_df.values.tolist()  #获取文件中所有节点
 
edge = []   #获取所有边
with open('E:/data/边.csv','r',encoding='utf-8-sig') as f: 
    data = f.readlines()  
    for line in data: 
        line = list(line.replace('\r','').replace('\n','').replace('\t','').split(','))
        # 去除“，”和换行符，将data列表中的元素转换为列表
        single_edge = tuple([line[0],line[1]])
        edge.append(single_edge)

为了更加直观理解每个变量内容，针对如下点与边的csv文件内容展示部分变量：

（2）点数据集与连边数据集展示

（3）变量格式展示

node_df，all_nodes_list，data格式如下

 line每一轮从列表data中获取一个元素，以第一轮为例，刚获取时格式如下：

  通过执行 line = list(line.replace('\r','').replace('\n','').replace('\t','').split(',')) ，将其中的逗号与换行符去除，并转换为列表，此时格式如下：

 通过执行 single_edge = tuple([line[0],line[1]]) ，提取line列表中的元素，并以元组形式储存于single_edge 中，此时格式如下：

 每个轮次将得到的single_edge内容存储于edge中，最终当所有轮次执行完后，edge内容如下：

 3.制定初始网络

 （1）具体代码如下

参数初始化设置

days = 50  # 设置模拟的天数
alpha = 0.2  # 感染率
beta = 0.10  # 恢复率

# 设置不同人群的显示颜色，易感者为橘色，感染者为红色，恢复者为绿色
color_dict = {"S": "orange", "I": "red", "R": "green"}

节点状态初始化设置

import networkx as nx
ba = nx.Graph()        # 引入一个类
ba.add_edges_from(edge)  # 将上一步的edge导入这个类中
for node in ba.nodes():  # 将每个人的初始状态设为“S”
    ba.nodes[node]["state"] = "S"
# 随机选取一个节点为初始感染者，此处设定为老张
ba.nodes["老张"]["state"] = "I"

（2）重要变量内容格式展示如下

仅使用了ba类中的 adj 与 nodes部分，每个人的adj中存储了与其有连接的人（即邻居），nodes中存储了每个人当前状态。

特别注意：类中数据类型为dict（字典）的数据部分设定完成后无法更改。

 4. 定义网络节点状态更新规则

（1）具体更新思想

先考虑单个节点的更新

我们使用一个简单的函数来实现一个节点的状态的更新。

首先，如果一个节点是恢复者，那么下一步还是恢复者，其节点状态保持不变。 如果一个节点是感染者，那么其恢复的概率是 β。用程序实现的方法为，先均匀生成一个0到1的随机数 p，如果 p < β，则节点恢复，否则节点依然处于感染状态。

如一个节点是易感者，先要去其邻居节点中看看一共有多少个邻居是感染者，有 k 个邻居是感染者，那么当前节点被感染的概率是 1 - (1 - α)k。我们生成一个0到1的随机数 p，如果 p < 1 - (1 - α)k，则节点被感染，否则不被感染。

（2）代码呈现如下

对单个节点更新部分的代码

import random
 
# 根据 SIR 模型，更新单一节点的状态
def updateNodeState(G,node, alpha, beta):
    if G.nodes[node]["state"] == "I": #感染者
        p = random.random() # 生成一个0到1的随机数
        if p < beta:   # gamma的概率恢复
            G.nodes[node]["state"] = "R" #将节点状态设置成“R”
    elif G.nodes[node]["state"] == "S": #易感者
        p = random.random() # 生成一个0到1的随机数
        k = 0  # 计算邻居中的感染者数量
        for neibor in G.adj[node]: # 查看所有邻居状态，遍历邻居用 G.adj[node]
            if G.nodes[neibor]["state"] == "I": #如果这个邻居是感染者，则k加1
                k = k + 1
        if p < 1 - (1 - alpha)**k:  # 易感者被感染
            G.nodes[node]["state"] = "I" 

通过遍历循环，实现对所有节点的状态更新：

def updateNetworkState(G, alpha, beta):  # 需要对应的ba，感染率，恢复率
    for node in G: #遍历图中节点，每一个节点状态进行更新
        updateNodeState(G,node, alpha, beta)   # 需要对应的ba，当前节点，感染率，恢复率

在每个时间单位下，当遍历更新完所有人当前状态后，用函数countSIR对3类人群的数量进行统计。

# 计算三类人群的数量
def countSIR(G):
    S = 0;I = 0
    for node in G:
        if G.nodes[node]["state"] == "S":
            S = S + 1
        elif G.nodes[node]["state"] == "I":
            I = I + 1
    return S,I, len(G.nodes) - S - I    

5.模拟执行过程并展示结果图

（1）执行部分代码展示

在图中开始SIR模型的模拟，设置模拟天数，开始执行模拟过程

import time
SIR_list = []
for t in range(0,days):
    updateNetworkState(ba,alpha,beta) #对网络状态进行模拟更新
    SIR_list.append(list(countSIR(ba))) #计算更新后三种节点的数量

（2）结果图展示部分代码

模型结果可视化

# 模拟天数为days，更新节点状态
import matplotlib.pyplot as plt

df = pandas.DataFrame(SIR_list,columns=["S","I","R"])
df.plot(figsize=(9,6),color=[color_dict.get("x") for x in df.columns])
plt.show()

（3）部分变量内容展示

将每一天的3类人群数量转换为一个列表，将每一天的列表放入SIR_list 中，最终 SIR_list 内容如下所示 ：

通过执行df = pandas.DataFrame(SIR_list,columns=["S","I","R"])，df内容如下所示：

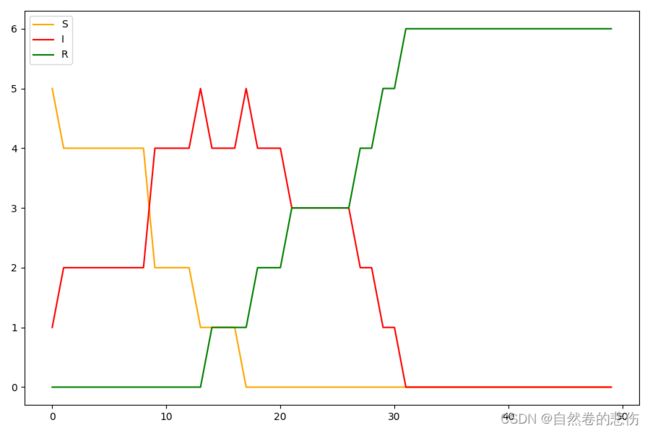
通过执行df.plot(figsize=(9,6),color=[color_dict.get(x) for x in df.columns]) ，将3类人群曲线得到不同颜色。

（4）结果图展示

---

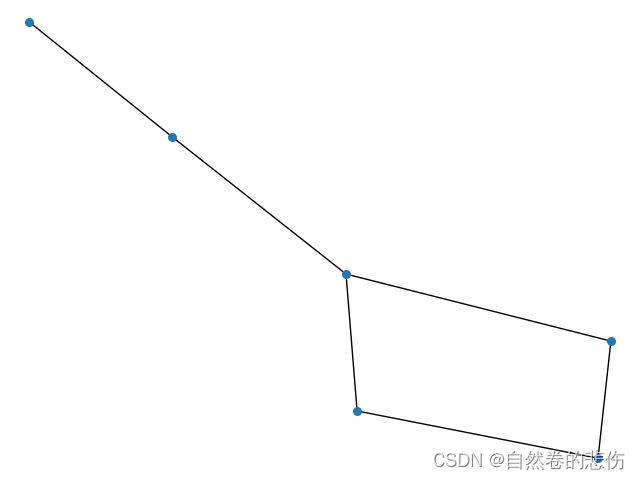
 三，通过python制作散点图

 在上述用python实现SIR模型的基础上，增添了散点图的呈现方式，更好地呈现了个体与个体之间的联系。

1.代码部分

ps=nx.spring_layout(ba)  #针对上述SIR模型中的ba类，布置框架
nx.draw(ba,ps,with_labels=False,node_size=30)  
# with_labels指是否给每个点设定标签，由于数据集中个体为人的名字，中文无法直接作为标签，故而设定为不需要
plt.show()

 2.散点图呈现