超简单易懂的模拟退火算法原理及其matlab代码实现

在介绍模拟退火算法之前，我们先认识一下爬山算法。

在爬山法寻找最优值的过程中，先随机生成一个点，计算其适应度值f(x)，然后再其左领域和右领域中依照步长各选取一个点计算其适应度值f(xleft),f(xright),比较其三者，将适应度最大值点作为下一次迭代的初始点，直至寻找到最大值点。

爬山算法是一种典型的贪婪算法是一种狭隘的没有顾及全局的算法，如图所示在使用爬山算法寻找最大值时容易陷入局部最优。

模拟退火算法原理

本文力求通俗易懂，故不在讲述物理层次的原理，我们回到爬山算法，爬山算法有一个非常重大的缺陷是容易陷入局部最优，并且陷入局部最优之后不能跳出。造成这样一种现象的原因是在每一次迭代中，我们采用贪婪的思想，只采用了最大值。

如图所示：按照爬山法的原理f(x)>f(xleft),所以将f(x)作为下一次迭代初值，而舍弃了可能更靠近全局最优值的f(xleft)。
所以引申出了一个议题：当左领域或者右领域的适应度值小于本身的适应度值，我们是否应该尝试去以一定的概率接受它来做下一次迭代的初值。

那么这个一定概率（p）到底是怎么计算的呢，按照咱们一般人的思维，当然是差距越小，咱们越容易去接受它。差距在函数寻找最优值的时候便体现在了距离上，即 | f(x)-f(xleft) | 也就是说这个概率是与这个距离成反比的，距离越大，接受的概率就越小。用数学的语言来表达即：
问题又来了，这个p既然是一个概率，那他也应该有个取值范围 [0,1] 这说明刚刚上式不能完全作为p的计算公式，那么在我们印象中有哪些函数的值域刚好是在[0,1]内，很多人可能想到sigmod。也有人想到arctan值域是在[-pi/2,pi/2],由于距离加了绝对值所以取值是在[0,pi/2],最后除以pi/2即可完成归一化。这些想法都是不错的，但是有一条更简单的曲线，它就是e^(-x)；图像如图：

那么结合距离和该函数图像就能合理的假设出

在这里，为什么不是倒数了是我们要保证距离和概率p要成负相关。

概率函数设计完毕工作到此似乎完成了，但是科学是严谨的。我们考虑一下现实，模拟退火算法模拟的是一种退温过程，我那稀薄的物理知识告诉我，分子在高温的情况下运动是非常剧烈的，在温度逐渐下降的过程中运动逐渐减缓并趋于稳定。

视角转移到算法这里，运动剧烈意味着我们更容易跳到其他地方搜索最优解，也就是在温度高的时候我们更容易接受其他解，可以合理的得到推论：概率p和温度成正相关，不妨设函数C(t)。此处记 | f(x)-f(xleft) | =△f。概率p公式可表现为：

其中C(t）是随着温度递减的函数。

到了这里终究还是逃不过物理范畴。因为的C(t)的选择是在太多了，哪一个才是合适的。在1995年Metropolis提出了一个重要的采样性方法，即设当前状态i生成新状态j，若新状态的内能小于状态i的内能即（Ej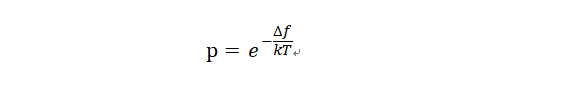
对这个准则有兴趣的话可以去查阅相关文献资料进行了解。博主微薄的物理知识实在是理解不了怎么得出的公式。

概率计算到此告一段落。既然是模拟退火算法，那温度变化必然是不可少的，且温度的变化应是随着时间而且减小的。下面介绍三种常用降温方式：
（1）T(k+1) =αT(k) 简易模拟退火算法

（2）T(k) = t0 /lg(1+k) 经典模拟退火算法

（3）T(k)= t0/(1+k) 快速模拟退火算法

算法流程

代码实现

%% SA 模拟退火: 求解函数y = 11*sin(x) + 7*cos(5*x)在[-3,3]内的最大值(动画演示）
tic
clear; clc

%% 绘制函数的图形
x = -3:0.1:3;
y = 11*sin(x) + 7*cos(5*x);
figure
plot(x,y,'b-')
hold on  % 不关闭图形，继续在上面画图

%% 参数初始化
narvs = 1; % 变量个数
T0 = 100;   % 初始温度
T = T0; % 迭代中温度会发生改变，第一次迭代时温度就是T0
maxgen = 200;  % 最大迭代次数
Lk = 100;  % 每个温度下的迭代次数
alfa = 0.95;  % 温度衰减系数
x_lb = -3; % x的下界
x_ub = 3; % x的上界

%%  随机生成一个初始解
x0 = zeros(1,narvs);
for i = 1: narvs
    x0(i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(1);    
end
y0 = Obj_fun1(x0); % 计算当前解的函数值
h = scatter(x0,y0,'*r');  % scatter是绘制二维散点图的函数（这里返回h是为了得到图形的句柄，未来我们对其位置进行更新）

%% 定义一些保存中间过程的量，方便输出结果和画图
max_y = y0;     % 初始化找到的最佳的解对应的函数值为y0
MAXY = zeros(maxgen,1); % 记录每一次外层循环结束后找到的max_y (方便画图）

%% 模拟退火过程
for iter = 1 : maxgen  % 外循环, 我这里采用的是指定最大迭代次数
    for i = 1 : Lk  % 内循环，在每个温度下开始迭代
        y = randn(1,narvs);  % 生成1行narvs列的N(0,1)随机数
        z = y / sqrt(sum(y.^2)); % 根据新解的产生规则计算z
        x_new = x0 + z*T; % 根据新解的产生规则计算x_new的值
        % 如果这个新解的位置超出了定义域，就对其进行调整
        for j = 1: narvs
            if x_new(j) < x_lb(j)
                r = rand(1);
                x_new(j) = r*x_lb(j)+(1-r)*x0(j);
            elseif x_new(j) > x_ub(j)
                r = rand(1);
                x_new(j) = r*x_ub(j)+(1-r)*x0(j);
            end
        end
        x1 = x_new;    % 将调整后的x_new赋值给新解x1
        y1 = Obj_fun1(x1);  % 计算新解的函数值
        if y1 > y0    % 如果新解函数值大于当前解的函数值
            x0 = x1; % 更新当前解为新解
            y0 = y1;
        else
            p = exp(-(y0 - y1)/T); % 根据Metropolis准则计算一个概率
            if rand(1) < p   % 生成一个随机数和这个概率比较，如果该随机数小于这个概率
                x0 = x1; % 更新当前解为新解
                y0 = y1;
            end
        end
        % 判断是否要更新找到的最佳的解
        if y0 > max_y  % 如果当前解更好，则对其进行更新
            max_y = y0;  % 更新最大的y
            best_x = x0;  % 更新找到的最好的x
        end
    end
    MAXY(iter) = max_y; % 保存本轮外循环结束后找到的最大的y
    T = alfa*T;   % 温度下降
    pause(0.01)  % 暂停一段时间(单位：秒)后再接着画图
    h.XData = x0;  % 更新散点图句柄的x轴的数据（此时解的位置在图上发生了变化）
    h.YData = Obj_fun1(x0); % 更新散点图句柄的y轴的数据（此时解的位置在图上发生了变化）
end

disp('最佳的位置是：'); disp(best_x)
disp('此时最优值是：'); disp(max_y)

pause(0.5)
h.XData = [];  h.YData = [];  % 将原来的散点删除
scatter(best_x,max_y,'*r');  % 在最大值处重新标上散点
title(['模拟退火找到的最大值为', num2str(max_y)])  % 加上图的标题

%% 画出每次迭代后找到的最大y的图形
figure
plot(1:maxgen,MAXY,'b-');
xlabel('迭代次数');
ylabel('y的值');
toc

function y = Obj_fun1(x)
    y = 11*sin(x) + 7*cos(5*x);
end

参考资料：张军，詹志辉《计算智能》 清华大学出版社
数学建模清风第二次直播：模拟退火算法
https://www.bilibili.com/video/BV1hK41157JL