数字图像处理MATLAB学习笔记（一）

数字图像处理MATLAB学习笔记（一）

灰度转换与空间滤波

本节主要使用Matlab语言进行灰度转换与空间滤波的使用

并对相关数学原理进行总结

1. Intensity Transformer Function(灰度转换函数)

这里Matlab语言中提供有多个灰度转换函数可使用。

灰度转换函数：输出值取决于像素点的大小。通过与特定参数进行比较，确定像素点位置输出像素大小是多少。

1.1 Function: imadjust & imcomplement

1.1.1 imadjust

Function model:

g = imadjust(f, [low_in high_in], [low_out high_out], gamma)

This function maps the intensity values in image f to new values in g, such that values between low_in and high_in map to values between low_out and high_out.

Valuse below low_in and above high_in are clipped; that is, values below low_in map to low_out, and those above high_in map to high_out. But do not worry about the class between the input and output image that they have the same one. If we use the empty matrix ([ ]) fr [low_in high_in] or for [low_out high_out] results in the default values [0 1]. Output intensity is reversed if high_out is less than low_out.

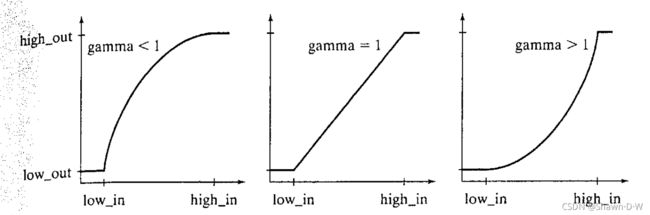
Another parameter: gamma specifies the shape of the curve that maps the intensity values in f to create g.

If gamma is less than 1, the mapping is weighted toward higher(brighter) output values. If gamma is larger than 1, the mapping is weighted toward lower(darker) output values. Gamma defaults to 1, which is linear mapping.

1.1.2 imcomplement(负片变换)

Function model:

g = imcomplement(f)

The negative of an image can be obtained also with fucntion imcomplement.

This function can tackle the problem the parameters high and low automatically.

一般情况下，我们使用此方法获得图片的负片图像

1.2 Logarithmic and Contrast-Stretching Transformations

Logarithm transformations are implemented using the expression

g = c * log(1 + double(f))

where c is a constant. The shape of this transformation is similar to the gamma curve with the low values set 0 and the high values set to 1 on both scales. Note that the shape of the gamma curve is variable(可变的), whereas the shape of the log function is fixed(固定的).

The easiest way to bring the resulting compressed values back to the full range of the display when performing a logarithmic in MATLAB is with the statement:

>> gs = im2uint8(mat2gray(g))

The function im2uint8 brings the values to the range [0, 1]. And im2uint8 brings the values to the range [0, 255].

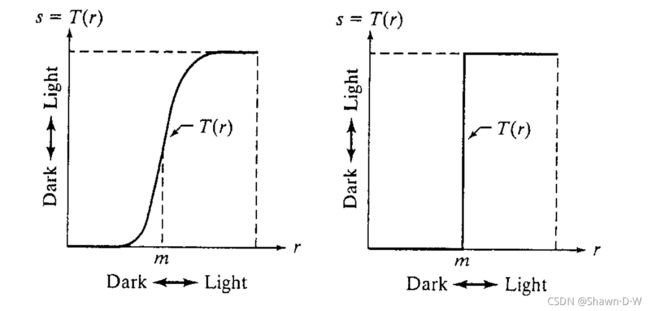
Contrast-stretching Transformation Function: It compressed the input levels lower than m into a narrow range of dark levels in the output image. The result is an image of higher contrast. (Show in left)

Function is
$$s=T(r)=\frac{1}{1+(m/r{)}^E}$$
Parameter r represents the intensities(灰度值) of the input image, parameter s the corresponding intensity values in the output image, and E controls the slope of the function. This equation is implemented in MATLAB for an entire image as

g = 1./(1 + (m. / (double(f) + eps)).^E)	

Note: The output values of image are limited in the range [0, 1] because the limited value of g is 1.

Thresholding Function: The output is a binary image in the limiting case show in right figure. It is a simple too used for image segmentation.

Example: Using a log transformation to reduce dynamic range

>> g = im2uint8(mat2gray(log(1 + double(f))));
>> imshow(g)

1.3 Specify any Intensity Transformations

If it is essential to use one specific transformation function to transform thr intensity of one image, T can be used as column vector that includes value of the transformation function. The program will be greatly simplified when using the float data ranging [0, 1] represents the input and output image. One easy implemented way is to use the interpl function.

z = linspace(0, 1, numel(T))';
g = interpl(z, T, f)

Parameter f represents the input image, g represents the output image, T represents the column vector with the same dimension to z.

1.4 Some Utility M-Function for Intensity Transformations

Two M-functions that incorporate various aspects of thei ntensity transformations introduced in the previous two sections.

1.4.1 Handling a Variable Number of Inputs and/or Outputs

To check the number of arguments input into an M-function, we use function nargin, which returns the actual number of arguments input into the M-function.

n = nargin

To check the number of arguments output into an M-function, we use function nargout, which returns the actual number of arguments input into the M-function.

n = nargout

Function nargchk can be used in the body of an M-function to check if the correct number of arguments were passed. The synax is:

msg = nargchk(low, high, number)

It returns the message NOT ENOUGH input parameters if number is less than low or TOO MANY input parameters if number is greater than high. If the number is between low and high(inclusive), nargchk returns an EMPTY matrix.

It is usually used to stop the execution via the error function if the incorrect number of arguments is input.

Often, it is useful to be able to write functions in which the number of input and/or output arguments is variable. We use the variables varagin and varargout.

For example, accepts a variable number of inputs into function testhv3,

function [m, n]  testhv3(varagin)

And returns a variable number of outputs from function testhv4.

function [varagout] = testhv4(m, n, p)

Anyway, it is one of the ways to handle the variable number of inputs and/or outputs.

1.4.2 Another M-Function for Intensity Transformations

It is a function that computes the following transformation functions: ***negative(负片变换)***, ***log(对数变换)***, gamma(gamma变换) and ***contrast stretching(对比度扩展)***.

function g = intrans(f, varargin)
% 亮度变换的M函数，实现负片变换、对数变换、gamma变换和对比度拉伸变换。
% 第三章 3.2.3
% G = INTRANS(F, 'neg') computes thr nrgative of input iamge F.
% 计算输入图像F的负数,即补图像
%
% G = INTRANS(F, 'log', C, CLASS) computes C * log(1 + F) and multiplies
% the result by (positive) constant C. CLASS : the class of output as
% 'unit8'/'uint16'.
% 实现对数转换
%
% G = INTERANS(F, 'gamma', GAM): a gamma transformation on the input iamge
% using parameter GAM.
% 实现gamma转换
%
% G = INTERANS(F, 'stretch', M, E): a contrast-stretching transformation
% using 1./(1 + (M ./(F+eps)).^E).  Parameter M [0, 1],default 
% M = mean2(im2double(F)), and E default to 4.
% 实现对比度拉伸

% varify the correct number of inputs
error(nargchk(2, 4, nargin))

% store the class of the input for use later
classin = class(f);

% If the input is of class double, and it is outside the range
% [0, 1], and the specified transformation is that 'log', convert the
% input to the range [0, 1].
if strcmp(class(f), 'double') & max(f(:) > 1) & ...
        ~strcmp(varargin{1}, 'log')
    f = mat2gray(f);
else % convert to double, regardless of class(f)
    f = im2double(f);
end

% Determine the type of transformation specifed.
method = varargin{1};
% Perform the intensity transformation specified.
switch method
    case 'neg'
        g = imcomplement(f);
    case 'log'
        if length(varargin) == 1
            c = 1;
        elseif length(varargin) == 2
            c = varargin{2};
        elseif length(varargin) == 3
            c = varargin{2};
            classin = varargin{3};
        else
            error('Incorrect number of inputs for the log option')
        end
        g = c * (log(1 + double(f)));
    case 'gamma'
        if length(varargin) < 2
            error('Not enough inputs for the gamma option')
        end
        gam = varargin{2};
        g = imadjust(f, [], [], gam);
    case 'stretch'
        if length(varargin) == 1
            % Use defaults
            m = mean2(f);
            E = 4.0;
        elseif length(varargin) == 3
            m = varargin{2};
            E = varargin{3};
        else
            error('Incorrect number of inputs for the stretch option.')
        end
        g = 1./(1 + (m./(f + eps)).^E);
    otherwise
        error('Unknow enhancement method');
end

% Convert to the class of the input image
g = changeclass(classin, g);

While, we may find out that there is no changeclass function in the MATLAB, so we need to finish it by coding. The code of function changeclass is supported by the author of the book and shown below:

function image = changeclass(class, varargin)
% CHANGECLASS changes the storage class of an image.
% I2 = CHANGECLASS(CLASS, I);
% RGB2 = CHANGECLASS(CLASS, RGB);
% BW2 = CHANGECLASS(CLASS, BW);
% X2 = CHANGECLASS(CLASS, X, 'indexed');

% Copyright 1993-2002 The MathWorks, Inc. Used with permission.
% $Revision: 1.2 $ $Date: 2003/02/19 22:09:58 $
switch class
    case 'uint8'
        image = im2uint8(varargin{:});
    case 'uint16'
        image = im2uint16(varargin{:});
    case 'double'
        image = im2double(varargin{:});
    otherwise
        error('Unsupported IPT data class.');
end

2 Histogram Processing and Function Plotting

This section is on obtaining, plotting, and using histograms for image enhancement.

2.1 Generating and Plotting Image Histograms

The hisgtogram of a digital image with $L$ total possible intensity levels in the range $[0,G]$ is defined as the discrete function
$$h(r_k)=n_k$$
where $r_k$ is the $kth$ intensity level in the interval $[0,G]$ and $n_k$ is the number of pixels in the image whose intensity level is $r_k$.

Often, it is useful to work with normalized histograms, obtained simply by dividing all elements of $h(r_k)$ by the total number of pixels in the image, which we denote by n:
$$p(r_k)=\frac{h(r_k)}{n}=\frac{n_k}{n}$$
We recognise $p(r_k)$ as an estimate of the probability of occurrence of intensity level $r_k$.

The core function in the toolbox for dealing with image histograms is imhist, the basic synax is

h = imhist(f, b)

Parameter f is the input image, h is its histogram $h(r_k)$, and b is the number of bins used in forming the histogram(b = 256 is used by default if it is not included in the argument). A bin is simply a subdivision of the intensity scale.

We obtain the normalized histogram simply by using the expression

p = imhist(f, b) / numel(f)

Note that numel(f) gives the number of elements in array f (i.e. the number of pixels in the image).

Histograms often are plotted using bar graphs. The function is

bar(horz, v, width)

Parameter v is a row vector containing the points to be plotted, horz is a vector of the same dimension as v that contains the increments of the horizontal scale, and width is a number between 0 and 1.

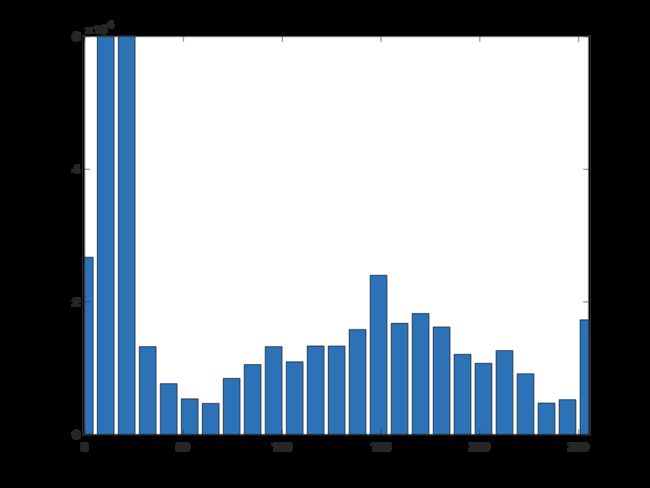
The following statement produce a bar graph, with the horizontal axis divided into groups of 10 levels:

>> h = imhist(flower, 25);
>> horz = linspace(0, 255, 25);
>> bar(horz, h)
>> axis([0 255 0 60000])
>> set(gca, 'xtick', 0:50:255)
>> set(gca, 'ytick', 0:20000:60000)

A stem graph is similar to a bar graph. The syntax is

stem(horz, v, 'color_linestyle_marker', 'fill')

Parameter v is row vector containing the points to be plotted, and horz is as described for bar. The argument ‘color_linestyle_marker’ is a triplet of values from Table below. The argument ‘fill’ is used for filling with the color in the marker.

Symbol	Color	Symbol	Line Style	Symbol	Marker
k	Black	-	Solid	+	Plus sign
w	White	–	Dashed	o	Circle
r	Red	:	Dotted	*	Asterisk
g	Green	-.	Dash-dot	.	Point
b	Blue	none	No line	x	Cross
c	Cyan			s	Square
y	Yellow			d	Diamond
m	Magenta			none	No marker

>> horz = 1:10:256;
>> stem(horz, h1, 'fill')
>> axis([0 255 0 15000])
>> set(gca, 'xtick', [0:50:255])
>> set(gca, 'ytick', [0:2000:15000])

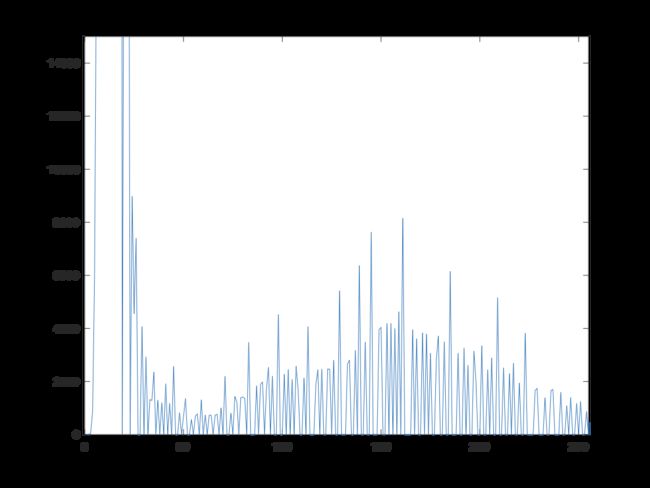
Function plot:

plot(horz, v, 'color_linestyle_marker')

It has similar parameters as stem graph.

>> h = imhist(flower);
>> plot(h) % Use the default values.
>> axis([0 255 0 15000])
>> set(gca, 'xtick', [0:50:255])
>> set(gca, 'ytick', [0:2000:15000])

2.2 Histogram Equalization

2.2.1 Continuous Quantities

If the intensity levels are continuous quantities normalised to the range [0, 1], and let $p_r(r)$ denote the probability density function(概率密度函数) of the intensity levels in a given image, where the subscript is used for differentiating between the PDFs of the input and output images.

So, the transformation on the input levels to obtain output intensity levels, s, is
$$s=T(r)={\int }_0^r{p}_r(w)dw$$
Parameter w is a dummy variable of integration(积分虚变量). And the probability density function of the output levels is uniform; that is,
$$p_s(s)=\{\begin{array}{l}1,\text{for 0 ≤ s ≤ 1}\\ 0,\text{otherwise}\end{array}$$
The preceding transformation generates an image whose intensity levels are equally likely. The net result of this intensity-level equalization process is an image with increased dynamic range, which will tend to have higher contrast.

2.2.2 Discrete Quantities

For discrete quantities we work with summations, and the quealization transformation becomes
$$s_k=T(r_k)=\sum _{j=1}^k{p}_r(r_j)=\sum _{j=1}^k\frac{n_j}{n}$$
for $k=1,2,\cdots ,L$ where $s_k$ is the intensity value in the output image corresponding to value $r_k$ in the input image.

Histogram equalization is implemented in the toolbox by function histeq, which has the syntax

g = histeq(f, nlev)

If parameter nlev is equal to $L$ (the total number of possible levels in the input image), then histeq implements the transformation function $T(r_k)$ directly. Unlike imhist, the default value in histeq is $nlev=64$.

If nlev is less than $L$, then histeq attempts to distribute the levels so that they will approximate a flat histogram.

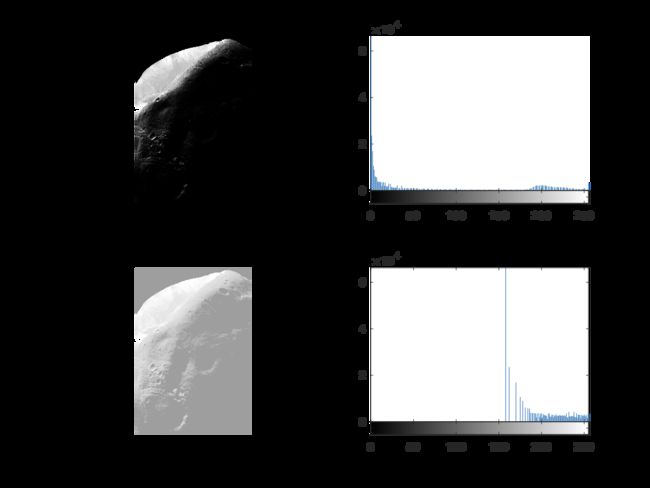
Example: Histogram equalization

>> imshow(f);
>> figure, imhist(f)
>> ylim('auto')
>> g = histeq(f, 256);
>> figure, imshow(g)
>> figure, imhist(g)
>> ylim('auto')

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rX04IwFz-1636876870758)(/Users/wanghe/Library/Application Support/typora-user-images/image-20211105181823083.png)]

Thr transformation function $T(r_k)$ is simply the cumulative sum of normalized histogram values. We can use function cumsum to obtain the transformation function.

>> hnorm = imhist(f)./numel(f);
>> cdf = cumsum(hnorm);

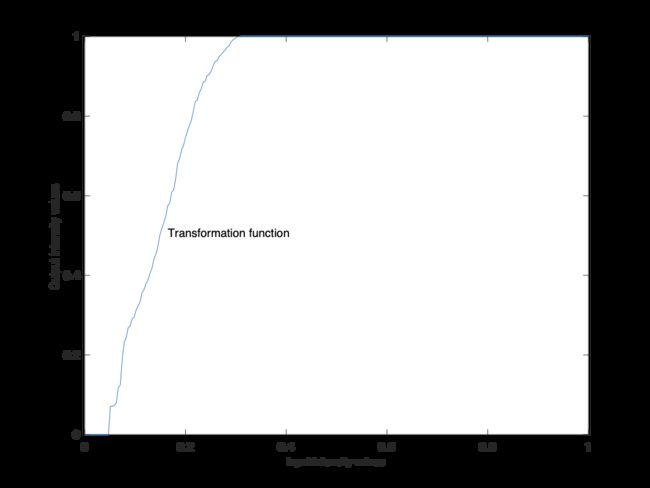
Then we can get the plot of the transformation function with cdf:

>> x = linspace(0, 1, 256);
>> plot(x, cdf)
>> axis([0 1 0 1]);
>> set(gca, 'xtick', 0:.2:1)
>> set(gca, 'ytick', 0:.2:1)
>> xlabel('Input intensity values', 'fontsize', 9)
>> ylabel('Output intensity values', 'fontsize', 9)

Conclusion: We can tell visually from this transformation function that a narrow range of input intensity levels is transformed into the full intensity scale in the output image.

2.3 Histogram Matching (Specification)

我们将生成具有特定直方图的图像的方法，称为直方图匹配法或直方图规定化。

原理辨析：

• 符号确定
  • $r$：输入图像灰度级
  • $z$：输出图像灰度级
  • $p_r(r)$：输入图像灰度级的概率密度函数
  • $p_z(z)$：输出图像灰度级的概率密度函数
  • $p_s(s)$：灰度级s具有均匀的概率密度函数
• 假设条件：
  • 变量$z$的特性：$H(z)={\int }_0^z{p}_z(w)dw=s$
• 寻找目的：
  • 寻找灰度级为$z$的图像，切具有特定的概率密度$p_z(z)$
• 推导结果：
  • $z=H^{-1}(s)=H^{-1}[T(r)]$

所以，只要能求出$H^{-1}$，就能够利用前面的灯饰得到变换后的灰度级$z$。

当处理离散值时，我们能够保证，若$p(Z_k)$是正确的直方图PDF(直方图具有单位面积且各亮度值均非负)，则$H$的反变换存在，且元素值非0。

一般使用***histeq***实现直方图匹配：

g = histeq(f, hspec)

参数***hspec***为特定的直方图，或者说是某个特定值的行向量。直方图金丝玉制定直方图***hspec***。当length(hspec)比图像f中的灰度级小很多时，输出图像g的直方图会较好地匹配hspec。

案例：直方图匹配

出现问题：直方图均衡化增强了图像灰度级，但是会造成“褪色”现象。

原因：低端过于集中的像素点映射到了灰度级的高端

补救方法：直方图匹配。期望的直方图在灰度级地段有较小的几种反胃，并能够保留原始图像直方图的大体形状。Histogram一般是双峰的，其中一个较大的模态在原点，另一个较小的模态在灰度级的高端。

这些类型的直方图可以被模型化，例如用多模态的高斯函数模拟。本次案例设计一个可以计算一个归一化到单位区域的双模态的高斯函数。

function p = twomodegauss(m1, sig1, m2, sig2, A1, A2, k)
%TWOMODEGAUSS Generates a two-mode Gaussian function.

c1 = A1 * (1 / ((2 * pi) ^ 0.5) * sig1);
k1 = 2 * (sig1^2);
c2 = A2 * (1 / ((2 * pi) ^ 0.5) * sig2);
k2 = 2 * (sig2 ^ 2);
z = linspace(0, 1, 256);
p = k + c1 * exp(-((z - m1) .^ 2) ./ k1) + ...
    c2 * exp(-((z - m2).^2) ./ k2);
p = p ./ sum(p(:));

2.4 Function adapthisteq

这个函数执行所谓的对比度受限的自适应直方图均衡(Contrast-Limitted Adaptive Histogram Equalization, CLAHE)。

该方法是由直方图规定化方法处理图像的小区域(小片)组成。然后用双线性插值将相邻小片组合起来以消除人工引入的边界效应。特别是可以先知均匀亮度区域的对比度，一面放大噪声。

Function syntax:

g = adapthisteq(f, param1, val1, param2, val2, ...)

• f：输入图像
• g：输出图像
• param/val：参数如下表所示

参数	值
‘NumTiles’	一个由正整数组成的两元素向量[r,c]，由向量的行和列指定小片数(将图片分割成r*c分块)。r和c都必须至少是2，小片总数等于r*c。默认值[8,8]
‘ClipLimit’	范围是[0,1]内的标量，用于指定对比度增强的限制，防止图像的同质区域出现过饱和现象。较高的值产生较强的对比度。默认值是0.01。
‘NBins’	针对建立对比度增强变黄所用的直方图容器数目指定的正整数标量。较高的值会在较慢的处理速度下导致较大的动态范围。默认值是256
‘Range’	规定输出图像数据范围的字符串： ‘original’——范围被限制到原始图像的范围，[min(f(: )) max(f(: ))]。‘full’——使用输出图像类的整个范围。例如，对于uint8类的数据，范围是[0 255]。这是默认值
‘Distribution’	字符串，用于指定图像小片所需的直方图形状： ‘uniform’——平坦的直方图（默认值），‘rayleigh’——钟形直方图，‘exponential’——曲线直方图
‘Alpha’	适用于瑞利和指数分布的非负标量。默认值为0.4

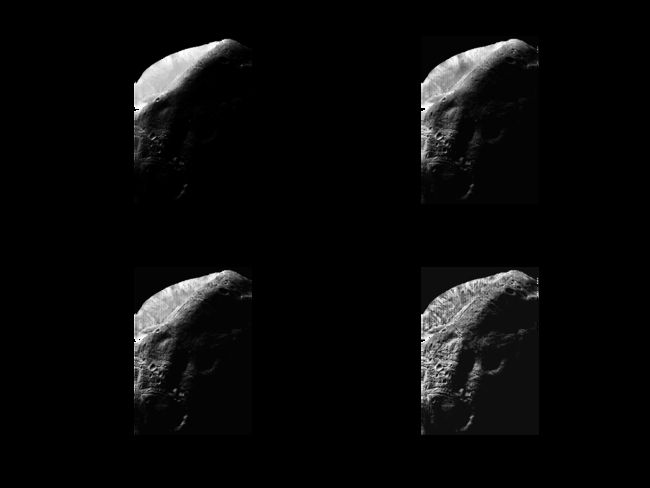
示例：

>> g1 = adapthisteq(f);
>> g2 = adapthisteq(f, 'NumTiles', [25 25]);
>> g3 = adapthisteq(f, 'NumTiles', [25 25], 'ClipLimit', 0.05);
>> subplot(221),imshow(f),title('原图像');
>> subplot(222),imshow(g1),title('默认值图像');
>> subplot(223),imshow(g2),title('设置参数NumTiles为[25 25]的图像');
>> subplot(224),imshow(g3),title('使用小片数量，且ClipLimit=0.05的图像');

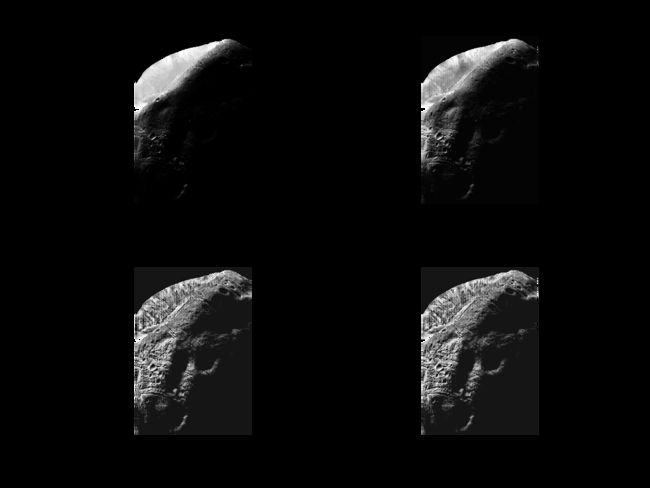
修改一些上述参数可得：

>> g1 = adapthisteq(f);
>> g2 = adapthisteq(f, 'NumTiles', [25 25], 'ClipLimit', 0.08);
>> g3 = adapthisteq(f, 'NumTiles', [25 25], 'ClipLimit', 0.08, 'NBins',255);
>> subplot(221),imshow(f),title('原图像');
>> subplot(222),imshow(g1),title('默认值图像');
>> subplot(223),imshow(g2),title('设置参数NumTiles为[25 25]的图像');
>> subplot(224),imshow(g3),title('使用小片数量，且ClipLimit=0.08的图像');

3 Spatial Filtering(空间滤波)

用于区别邻域更新和输出映射的常见的处理方式是空间滤波。

若对邻域中像素的计算是线性的，则运算称为线性的，则运算称为线性空间滤波（空间卷积）；否则称运算为非线性空间滤波。

3.1 Linear Spatial Filtering

一维：一个函数***f***和一个掩模***w***

**相关(corr)：**就是在图像f中逐点移动滤波掩模w然后相应的值乘积然后累加得到的响应值

卷积(conv)：将掩模旋转*180度，再逐点移动然后相应的值乘积相加得到响应值。(没有旋转只有乘积求和就不叫卷积运算*)

区别：

• 相关：如果固定w，让f在w 上移动，结果将会不同，因而顺序也是有关系的。

• 与相关不同的是，颠倒f的顺序会产生相同的卷积结果，这是因为其中一个函数总会在卷积中旋转180度。

• 如果对称移动函数f，则卷积和相关这两个操作会产生相同的结果。

表达式：

• 相关：

$$w(x,y)\star f(x,y)=\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)f(x+s,y+t)$$

• 卷积：

$$w(x,y)\odot f(x,y)=\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)f(x-s,y-t)$$

Note: 这里公式右边的减号反转了$f$（即旋转180度），主要是为了便于表示。

Function imfilter：

g = imfilter(f, w, filtering_mode, boundary_options, size_options)

参数信息：

• f：输入图像
• w：滤波模版（卷积核）
• g：滤波结果
• filtering_mode：默认corr(相关)，conv表示卷积
• boundary_options：处理边界填充问题。常用‘replicate’通过复制外边界的值来扩展。
• size_options：same或full。

如使用既非预先旋转又非对称的滤波器时，只希望执行卷积，可以使用下列语法：

>> g = imfilter(f, w, 'conv', 'replicate')
>> g = imfilter(f, rot90(w, 2), 'replicate') % rot90(w, 2)表示把w旋转180度

一般情况下，为了追求更高的精度，我们会使用im2single、im2double、tofloat函数将f转换为浮点数。

3.2 Nonlinear Spatial Filtering

线性空间滤波基于计算乘积和（线性操作），非线性空间滤波基于涉及邻域像素内的非线性操作。

两个通常的非线性滤波操作函数：

1. Function nlfilter：直接执行二维操作
2. Function colfilt：按列组织数据。内存消耗大，运算速度快，更为常用。

colfilt语法：

g = colfilt(f, [m n], 'sliding', fun)

参数信息：

• f：输入图像。
• g：滤波结果。
• m n：滤波区域维数。
• ‘sliding’：表明处理过程时m*n区域在输入图像f中逐像素滑动。
• fun：函数具柄。

一般情况下，在使用colfilt前，需要对f进行padding，常用到function padarray。

fp = padarray(f, [r c], method, direction)

参数信息：

• f：输入图像。
• fp：填充结果。
• r c：用于填充f的行数和列数
• method：确定填充方法
  • symmetric：通过镜像映射在边界的对面padding
  • replicate：通过复制值在边界的外部padding
  • circular：通过把图像处理成2D周期函数的一个周期padding
• direction：确定填充方向
  • pre：每一维，第一个元素之前padding
  • post：每一维，最后一个元素之后padding
  • both：每一维，第一个之前和最后一个之后padding。函数默认值

4 Image Processing Toolbox Standard Spatial Filterss

4.1 Linear Spatial Filters线性空间滤波器

我们可以通过函数fspecial实现一些滤波器，这个函数可以生成滤波模版w。

w = fspecial('type', parameters)

参数信息：

• ‘type’：滤波器的类型
• ‘parameters’：指定滤波器

Type	Syntax and Parameters
average	均值滤波，参数为n，代表模版尺寸，用向量表示，默认值为[3,3]
disk	圆形平均滤波器（包含在变长为2r+1大小的正方形内），半径为r。默认半径为5
gaussian	高斯低通滤波器，参数有两个，n表示模版尺寸，默认值为[3,3]，sigma表示滤波器的标准差，单位为像素，默认值为0.5。
laplacian	拉普拉斯算子，参数为alpha，用于控制拉普拉斯算子的形状，取值范围为[0,1]，默认值为0.2。
log	拉普拉斯高斯算子，参数有两个，n表示模版尺寸，默认值为[3,3]，sigma为滤波器的标准差，单位为像素，默认值为0.5
prewitt	prewitt算子，用于边缘增强，无参数。
sobel	著名的sobel算子，用于边缘提取，无参数。
unsharp	对比度增强滤波器，参数alpha用于控制滤波器的形状，范围为[0,1]，默认值为0.2。

Example 使用imfilter实现拉普拉斯滤波器

拉普拉斯算子是n纬欧几里得空间的一个二阶微分算子，定义为梯度的散度。在笛卡尔系下可定义为xi中的所有非混合二阶偏导数的和
$$\Delta f={\nabla }^{2}f=\sum _{i=1}^n\frac{{\partial }^{2}f}{\partial x^2}$$
图像拉普拉斯算子定义为
$$\Delta f(x,y)={\nabla }^{2}f(x,y)=\frac{{\partial }^{2}f(x,y)}{\partial x^2}+\frac{{\partial }^{2}f(x,y)}{\partial y^2}$$
通常，二阶导数的数字近似为：
$$\begin{gathered} \frac{{\partial }^{2}f(x,y)}{\partial x^2}=f(x+1,y)+f(x-1,y)-2f(x,y) \\ \frac{{\partial }^{2}f(x,y)}{\partial y^2}=f(x,y+1)+f(x,y-1)-2f(x,y) \end{gathered}$$
所以有：
$${\nabla }^{2}f(x,y)=[f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)]-4f(x,y)$$
这个表达式可以在图像中所有点都实现，前提是使用如下卷积核$\begin{array}{ccc}0& 1& 0\\ 1& -4& 1\\ 0& 1& 0\end{array}$ 或 $\begin{array}{ccc}1& 1& 1\\ 1& -8& 1\\ 1& 1& 1\end{array}$。

使用拉普拉斯算子增强图像的基本公式可以写为
$$g(x,y)=f(x,y)+c[{\nabla }^{2}f(x,y)]$$
参数信息：

• $f(x,y)$：输入图像
• $g(x,y)$：增强后图像
• $c$：如果mask的中心细数为正，$c=1$；否则$c=-1$

Note：因为Laplacin是微分算子，是图像瑞华，并使恒定区域为0。所以，把结果和原始图叠加可以恢复灰度级色调。

Function fspecial实现Laplacin Mask的模版：
$$\text{fspecial(’laplacian’, alpha)}=\begin{array}{ccc}\frac{\alpha }{1+\alpha }& \frac{1-\alpha }{1+\alpha }& \frac{\alpha }{1+\alpha }\\ \frac{1-\alpha }{1+\alpha }& \frac{-4}{1+\alpha }& \frac{1-\alpha }{1+\alpha }\\ \frac{\alpha }{1+\alpha }& \frac{1-\alpha }{1+\alpha }& \frac{\alpha }{1+\alpha }\end{array}$$
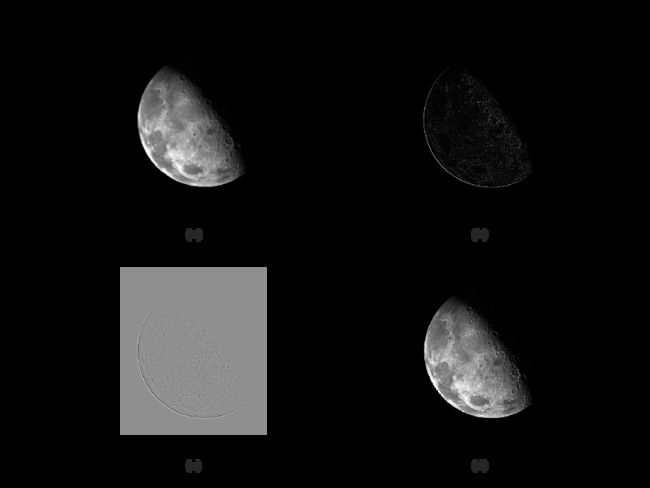
代码示例：

>> w = fspecial('laplacian', 0);
>> g1 = imfilter(moon, w, 'replicate');
>> imshow(g1, [])
>> moon2 = tofloat(moon);
>> g2 = imfilter(moon2, w, 'replicate');
>> g = moon2 - g2;
>> imshow(g)

可以看出图(d)比图(a)锐化效果更明显。

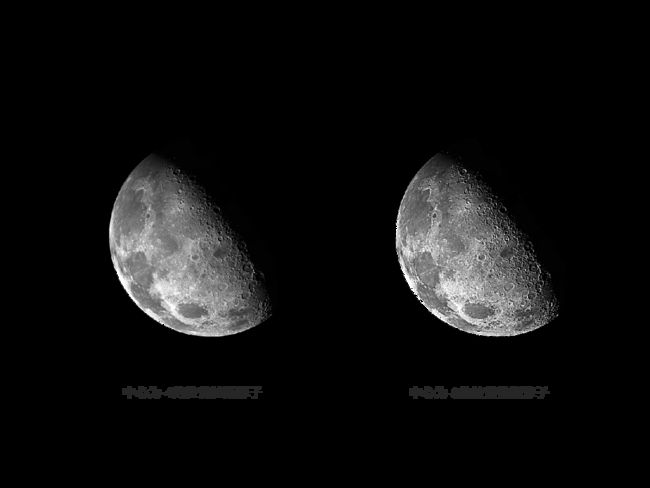
Example 人工规定的滤波器与增强技术的比较

这里用卷积核$\begin{array}{ccc}0& 1& 0\\ 1& -4& 1\\ 0& 1& 0\end{array}$ 和 $\begin{array}{ccc}1& 1& 1\\ 1& -8& 1\\ 1& 1& 1\end{array}$ 的滤波效果做比较。

>> w4 = fspecial('laplacian', 0); % -4 in the center
>> w8 = [1 1 1; 1 -8 1; 1 1 1];
>> g4 = moon2 - imfilter(moon2, w4, 'replicate');
>> g8 = moon2 - imfilter(moon2, w8, 'replicate');
>> imshow(g4);
>> imshow(g8);

中心为-8的拉普拉斯滤波器增强后的图像比中心为-4强化的图像更清晰。

4.2 Nonlinear Spatial Filters

Function ordfilt2：是一种order-statistic filters（统计顺序/排序滤波器）

g = ordfilt2(f, order, domain)

参数：

• f：输入图像
• g：输出图像
• order：用邻域排序集合中的第order个元素替代f中的每个元素
• domain：非零元素指定邻域。domain是一个m*n的0/1矩阵，并决定计算中使用的邻域中像素点的位置。

Function medfilt2：二维中值滤波器

g = medfilt2(f, [m n], padopt)

参数：

• f：输入图像
• g：输出图像
• [m n]：定义用于计算中值的尺寸为m*n的邻域，默认3*3
• padopt：规定三个可能的padding
  • ‘zeros’：默认值
  • ‘symmetric’：镜像反射padding
  • ‘indexed’：如果f是double类，填充1，否则0

Example 利用函数medilt2的中值滤波

>> board = imread('../ch05/Fig0507(a)(ckt-board-orig).tif');
>> subplot(2,2,1);imshow(board);xlabel('(a)');
>> boardn = imnoise(board, 'salt & pepper', 0.2); % 添加黑白噪音点
>> subplot(2,2,2);imshow(boardn);xlabel('(b)');
>> gm = medfilt2(boardn); % 对待噪声图像进行中值滤波
>> subplot(2,2,3);imshow(gm);xlabel('(c)');
>> gms = medfilt2(boardn, 'symmetric'); % 对待噪声图像进行中值滤波，并进行0填充，减弱黑点噪声影响
>> subplot(2,2,4);imshow(gms);xlabel('(d)');

5 Using Fuzzy Techniques for Intensity Transformations and Spatial Filtering

5.1 Fuzzy Set(模糊集合)

定义：无限制隶属度函数称为模糊集的基础，使用模糊逻辑生成的集合视为模糊集合。

令 $Z$ 为元素或对象的集合，$z$ 表示 $Z$ 的元素；即$Z=\{z\}$。

$Z$ 中的模糊集合 $A$ 由隶属度函数 ${\mu }_A(z)$ 来描述。

对于来自 $Z$ 的某个具体元素 $z_0$ ，${\mu }_A(z_0)$ 的值表示 $A$ 中 $z_0$ 的隶属度等级。

模糊集合 $A$ 是由 $z$ 和隶属度函数组成的有序对，隶属度函数为 $A$ 中的每个 $z$ 指定隶属资格等级：
$$A=\{z,{\mu }_A(z)|z\in Z\}$$
和概率论不同的是：

• 概率论：一个人是年轻人有50%的几率
• 模糊语句：在年轻人的集合中，一个人的隶属级别为0.5

使用范围：以模糊和不精确为特点的情况，而不是随机情况

相关定义：

• 空集：当且仅当Z中的隶属度函数为0时，模糊集合为空
• 相等：当且仅当所有$z\in Z,{\mu }_A(z)={\mu }_b(z)$时，模糊集合A和B是相等的，记为A=B
• 补集：模糊集合A的补集记为：$\overline{A}=NOT(A)$，隶属度函数为：${\mu }_{\overline{A}}(z)=1-{\mu }_A(z)$
• 子集：当且仅当所有$z\in Z$时，都有${\mu }_A(z)\le {\mu }_B(z)$，模糊集合A是B的子集
• 并集：对于所有的$z\in Z$，模糊集合A和B的交集记为$A\cup B=AORB$，隶属度函数为${\mu }_U(z)=max[m{u}_A(z),{\mu }_B(z)]$
• 交集：对于所有的$z\in Z$，模糊集合A和B的交集记为$A\cap B=AANDB$，隶属度函数为${\mu }_I(z)=max[m{u}_A(z),{\mu }_B(z)]$

5.2 一组自定义的模糊M-Function

5.2.1 MATLAB Nested Function嵌套函数

Nested Function中使用或定义的变量驻留在最外层函数的工作空间，最外层函数包含nested function，并可以访问变量。

基本语法：

function [outputs1] = outer_function(arguments1)
statements
	function [outputs2] = inner_function(arguments2)
		statements
	end
statements
end

5.2.2 Membership Function 隶属度函数

function mu = triangmf(z, a, b, c)
%TRIANGMF Triangular membership function
%   MU = TRIANGMF(Z, A, B, C) computes a fuzzy membership function
%   with a triangular shape. Z is the input variable and can be a
%   vector of any length. A, B, and C are scalar parameters, such
%   that B >= A and C >= B, that define the triangular shape.
%   
%       MU = 0,                         Z < A
%       MU = (Z - A) ./ (B - A),        A <= Z < B
%       MU = 1 - (Z - B) ./ (C - B),    B <= Z < C
%       MU = 0,                         C <= Z

mu = zeros(size(z));

low_side = (a <= z) & (z < b);
high_side = (b <= z) & (z < c);

mu(low_side) = (z(low_side) - a) ./ (b - a);
mu(high_side) = 1 - (z(high_side) - b) ./ (c - b);


function mu = trapezmf(z, a, b, c, d)
%TRAPEZMF Trapezoidal membership function
%   MU = TRAPEZMF(Z, A, B, C, D) computes a fuzzy membership function
%   with a trapezodial shape. Z is the input variable and can be a
%   vector of any length. A, B, C, and D are scalar parameters that
%   define the trapezodial shape. The parameters must be ordered so
%   that A <= B, B <= C, C <= D.
% 
%       MU = 0,                         Z < A
%       MU = (Z - A) ./ (B - A),        A <= Z < B
%       MU = 1,                         B <= Z < C
%       MU = 1 - (Z - C) ./ (D - C),    C <= Z < D
%       MU = 0,                         D <= Z

mu = zeros(size(z));

up_ramp_region = (a <= z) & (z < b);
top_region = (b <= z) & (z < c);
down_ramp_region = (c <= z) & (z < d);

mu(up_ramp_region) = 1 - (b - z(up_ramp_region)) ./ (b - a);
mu(top_region) = 1;
mu(down_ramp_region) = 1 - (z(down_ramp_region) - c) ./ (d - c);


function mu = sigmamf(z, a, b)
%SIGMAMF Sigma membership function
%   MU = SIGMAMF(Z, A, B) computes a sigma fuzzy membership
%   function. Z is the input variable and can be a vector of 
%   any length. A and B are scalar parameters, ordered
%   such that A <= B.
%   
%       MU = 0,                         Z < A
%       MU = (Z - A) ./ (B - A),        A <= Z < B
%       MU = 0,                         B <= Z
%   
%   Note: sigmamf is a special case of the trapezodial function

mu = trapezmf(z, a, b, inf, inf);


function mu = smf(z, a, b)
%SMF S-shaped membership function
%   MU = SMF(Z, A, B) computes the S-shaped fuzzy membership
%   function. Z is the input variable and can be a vector of any
%   length. A and B are scalar shape parameters, ordered such that 
%   A <= B.
%   
%       MU = 0,                             Z < A
%       MU = 2*((Z - A) ./ (B - A)).^2,     A <= Z < P
%       MU = 1 - 2*((Z - B) ./ (B - A)).^2, P <= Z < B
%       MU = 0,                             B <= Z
% 
%   where P = (A + B) / 2

mu = zeros(size(z));

p = (a + b) / 2;
low_range = (a <= z) & (z < p);
mu(low_range) = 2 * ( (z(low_range) - a) ./ (b - a)).^2;

mid_range = (p <= z) & (z < b);
mu(mid_range) = 1 - 2 * ( (z(mid_range ) - b) ./ (b - a)).^2;

high_range = (b <= z);
mu(high_range) = 1;

function mu = bellmf(z, a, b)
%BELLMF Bell-shaped membership function
%   MU = BELLMF(Z, A, B) computes the bell-shaped fuzzy membership
%   function. Z is the input variable and can be a vector of any
%   length. A and B are scalar shape parameters, ordered such that 
%   A <= B.
%   
%       MU = SMF(Z, A, B),       Z < B
%       MU = SMF(2*B - Z, A, B), B <= Z

mu = zeros(size(z));

left_side = z < b;
mu(left_side) = smf(z(left_side), a, b);

right_side = z >= b;
mu(right_side) = smf(2*b - z(right_side), a, b);

function mu = truncgaussmf(z, a, b, s)
%TRUNCGAUSSMF Truncated Gaussian membership function
%   MU = TRUNCGAUSSMF(Z, A, B, S) computes a truncated Gaussian
%   fuzzy membership function. Z is the input variable and can be a
%   vector of any length. A, B, and S are scalar shape parameters. A
%   and B have to be ordered such that A < B.
%   
%       MU = exp(-(Z - B).^2 / s^2), abs(Z-B) <= (B - a)
%       MU = 0,                      otherwise

mu = zeros(size(z));

c = a + 2 * (b - a);
range = (a <= z) & (z <= c);
mu(range) = exp(-(z(range) - b).^2 / s^2);

5.2.3 Function for computing rule strengths 计算规则强度的函数

function L = lambdafcns(inmf, op)
%LAMBDAFCNS Lambda functions for a sett of fuzzy rules
%    L = LAMBDAFCNS(INMF, OP) create a set of lambda functions
%    (rule strength functions) corresponding to a set of fuzzy rules.
%    L is a cell array of function handles. IMNF is an M-by-N matrix
%    of input membership function handles. M is the number of rules, 
%    and N is the number of fuzzy system inputs. INMF(i, j) is the 
%    input membership function applied by the i-th rule to the j-th
%    input. 
%    
%    OP is a function handle used to combine the antecedents for each
%    rule. OP can be either @min or @max. If monitted, the default
%    value for OP is @min.
% 
%    The output lambda functions are called later with N inputs,
%    Z1, Z2, ..., ZN, to determine rule strength:
% 
%        lambda_i = L{i}(Z1, Z2, ..., ZN)

if nargin < 2
    % Set default operator for combining rule antecedents
    op = @min;
end

num_rules = size(inmf, 1);
L = cell(1, num_rules);

for i = 1:num_rules
    % Each output lambda function calls the ruleStrength() function
    % with i (to identify which row of the rules matrix should be
    % used), followed by all the Z input arguments (which are passed
    % along via varargin).
    L{i} = @(varargin) ruleStrength(i, varargin{:});
end

    %--------------------------------------------------------%
    function lambda = ruleStrength(i, varargin)
        % lambda = ruleStrength(i, Z1, Z2, Z3, ...)
        Z = varargin;
        % Initialize lambda as the output of the first membership
        % function of the k-th rule
        memberfcn = inmf{i, 1};
        lambda = memberfcn(Z{1});
        for j = 2:numel(varargin)
            memberfcn = inmf{i, j};
            lambda = op(lambda, memberfcn(Z{j}));
        end
    end

end

5.2.4 Function for performing implications 执行推断函数

function Q = implfcns(L, outmf, varargin)

Z = varargin;

num_rules = numel(L);
Q = cell(1, numel(outmf));

for i = 1:num_rules
    lambdas(i) = L{i}(Z{:});
end

for i = 1:num_rules
    Q{i} = @(v) implication(i, v);
end

if numel(outmf) == (num_rules + 1)
    Q{num_rules + 1} = @elesRule;
end

    %-------------------------------------------------------%
    function q = implication(i, v)
        q = min(lambdas(i), outmf{i}(v));
    end
    
    %-------------------------------------------------------%
    function q = elseRule(v)
        lambda_e = min(1 - lambdas);
        q = min(lambda_e, outmf{end}(v));
    end

end

5.2.5 Function for performing aggregation 执行合并的函数

function Qa = aggfcn(Q)

Qa = @aggregate;

    function q = aggregate(v)
        q = Q{1}(v);
        for i = 2:numel(Q)
            q = max(q, Q{i}(v));
        end
    end

end

5.2.6 Function for performing defuzzification 执行去模糊的函数

function out = defuzzify(Qa, vrange)

v1 = vrange(1);
v2 = vrange(2);

v = linspace(v1, v2, 100);
Qv = Qa(v);
out = sum(v .* Qv) / sum(Qv);
if isnan(out)
    out = mean(vrange);
end

end

5.2.7 Putting it all together

function F = fuzzysysfcn(inmf, outmf, vrange, op)

if nargin < 4
    op = @min;
end

L = lambdafcns(inmf, op);

F = @fuzzyOutput;

    %-------------------------------------------------------%
    function out = fuzzyOutput(varargin)
        Z = varargin;
        Zk = cell(1, numel(Z));
        out = zeros(size(Z{1}));
        for k = 1:numel(Z{1})
            for p = 1:numel(Zk)
                Zk{p} = Z{p}(k);
            end
            Q = implfcns(L, outmf, Zk{:});
            Qa = aggfcn(Q);
            out(k) = defuzzify(Qa, vrange);
        end
    end

end

5.2.8 性能改进

function G = approxfcn(F, range)

num_inputs = size(range, 1);
max_table_elements = 10000;
max_table_dim = 100;

table_dim = min(floor(max_table_elements^(1/num_inputs)), ...
    max_table_dim);

inputs = cell(1, num_inputs);
grid = cell(1, num_inputs);
for k = 1:num_inputs
    grid{k} = linspace(range(k, 1), range(k, 2), table_dim);
end

if num_inputs > 1
    [inputs{:}] = ndgrid(grid{:});
else
    inputs = grid;
end

table = zeros(size(inputs{1}));

bar = waitbar(0, 'Working');

Zk = cell(1, num_inputs);
L = numel(inputs{1});
% Update the progress bar at 2% intervals
for p = 1:L
    for k = 1:num_inputs
        Zk{k} = inputs{k}(p);
    end
    table(p) = F(Zk{:});
    if (rem(p, wait_update_interval) == 0)
        % Update the progress bar
        waitbar(p/L);
    end
end
close(bar);

G = @tableLookupFcn;

    %--------------------%
    function out = tableLookupFcn(varargin)
        if num_inputs > 1
            out = interpn(grid{:}, table, varargin{:});
        else
            out = interp1(grid{1}, table, varargin{1});
        end
    end
    
end