三维重建总结

基于多视角图像的三维重建

• 基于体像素的三维重建算法
• 基于深度图的三维重建算法
• 基于特征点生长的三维重建算法：基于特征点生长的三维重建技术，通过对现实场景进行图像采集，然后对多幅图像进行特征点检测，匹配，生成稀疏种子点云，并在此基础上增加生长点有条件的初值矫正优化等措施，提高重建的精确性，降低噪声、空洞等引起的重建错误。

三维场景渲染与重建是利用场景的图形或图像等信息渲染出特定观测视点的场景图像和重建出三维场景的结构模型，它是计算机视觉中的一个重要的研究课题，开展该方面的研究对于模型识别、虚拟现实、探险救援、军事侦察等都具有非常重要的意义。经典的三维场景渲染与重建方法按照基本处理单位的不同分为：

以像素点作为基本处理单位逐点进行渲染与重建，该方法获得的渲染图像和重建模型比较真实，但是速度较慢；

以网格作为基本处理单位进行渲染与重建，该计算速度较快，基本能满足实时渲染的要求，但是当网格内包含目标边界时导致渲染图像和重建模型失真。

另外，现有的诸多渲染与重建算法均要求已知不同观测视点的坐标，而现实情况下并不一定能精确获得视点的坐标，例如水下机器人受水流冲击影响，在拍摄时坐标很难确定。本文是以图像粒（即连通区域）作为基本处理单位，研究基于空间多视点图像的三维场景渲染与重建技术。主要研究内容包括：

（1）基于形态学连通性理论的粒化研究
考虑到图像的色相，亮度和纹理等特性，提出了利用形态学属性连通算子研究彩色图像的粒化方法，每个粒代表了一个不规则形状的连通区域。同一粒的内部像素点具有同质性或相同的纹理结构，不同粒中像素点的值具有不同的特性。探讨了基于马尔科夫模型的粒边界确定方法，降低了视角，光照对彩色图像粒化的影响。
（2）基于空间拓扑结构的图像配准研究
建立了基于有向图的图像粒（连通区域）空间拓扑结构关系，引入可达矩阵分析拓扑结构图中有向树和有向回路（即广义顶点）的特点。将图像粒进行模糊化，探讨了基于模糊推理的不同视点间图像粒的全局最佳匹配问题，在图像粒匹配的基础上，分析粒内特征点匹配关系，建立了匹配粒内像素点的单应映射。该方法消除了具有自相似结构的不同视点图像间错误匹配问题。
（3）在未知多视点相机位置关系的前提下，实现三维场景渲染和重建
针对相机径向畸变等因素的影响，提出了基于加权sampson近似的不同视点相机间相对位置计算方法。提出了基于视图张力漂移的场景深度估计方法，并且研究了基于图像粒的空间变换与场景深度图相结合的三维场景渲染方法，研究了模拟表面拟合与点云模型修正相结合的三维模型重建技术。上述方法在未知多视点相对位置关系的前提下，降低了累计误差的影响，能够比较真实的实现三维场景的渲染与重建。

基于RGBD的三维重建：
简单地说，三维重建就是从输入数据中建立3D模型。其中，在面向消费者层面的深度相机出现以前，三维重建技术的输入数据通常只有RGB图像。通过对物体的不同角度拍摄的RGB图像，使用相关的计算机图形学和视觉技术，我们便可以重建出该物体的三维模型。不过，早期的三维重建技术得到的模型精度往往较低，且技术的适用范围有限。消费者层面的深度相机的出现为三维重建技术提供了深度图像数据，大大降低了重建的难度，并使得三维重建技术可以应用到几乎任何场景。

深度值和三维数据
对于现实场景中的点，深度相机扫描得到的每一帧数据不仅包括了场景中的点的彩色RGB图像，还包括每个点到深度相机所在的垂直平面的距离值。这个距离值被称为深度值（depth），这些深度值共同组成了这一帧的深度图像。也就是说，深度图像可以看作是一幅灰度图像，其中图像中每个点的灰度值代表了这个点的深度值，即该点在现实中的位置到相机所在垂直平面的真实距离。

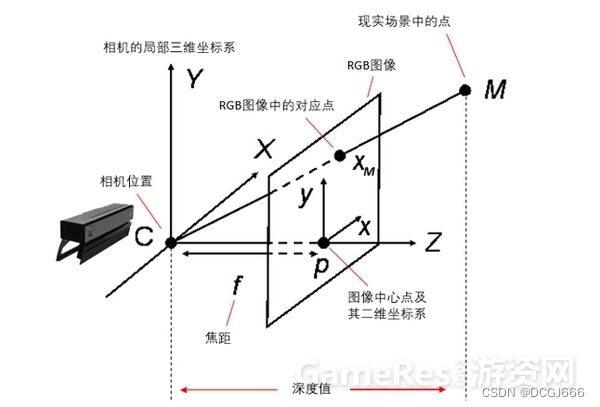
如图所示，对于现实场景中点M，深度相机能够获取其在RGB图像中的成像点XM，以及M到相机所在的垂直平面（即XY平面）的距离，这个距离便是M的深度值。以相机位置为原点，相机所朝方向为Z轴，相机的垂直平面的两个轴为X、Y轴，可以建立相机的局部三维坐标系。另外，RGB图像到相机位置的距离正是相机的焦距。通过这些数据并使用简单的三角几何公式，我们很容易得到M在相机的局部坐标系中的三维坐标。于是，RGB图像中的每个点，都会对应一个在相机的局部坐标系中的三维点。因此，深度相机的每一帧的深度图像就相当于一个在相机的局部三维坐标系中的点云模型。

基于深度相机的三维重建的核心问题

如果输入的RGBD数据只有一帧，那么只需要把这一帧对应的点云模型作为重建的模型输出即可。不过，通常的深度相机的帧率（FPS）普遍较高，所带来的数据量是非常庞大的。以微软的Kinect v1为例，其FPS=30，即1秒钟扫描30帧，也就是1秒钟便可得到30张RGB图像和30张深度图像。每一帧图像的分辨率通常是640x480，那么在短短的1秒钟，深度相机得到的点云的点的个数是640x480x30=9216000.

如何解决如此庞大的数据？——>另外，深度相机所得到的深度数据是存在误差的，即使相机位置固定，现实场景中的点在不同帧中的深度值也会有区别。也即是说，对于每一个现实中的点，在扫描过程中会得到众多“测量值”位置，那么，如何估计点的最终位置？这个问题可以被称为“从大数据中建立模型”问题。

重建过程中还有一个关键性问题——相机位置的估计。首先，为什么需要估计相机位置？通过本文之前内容讲述的深度值的原理可知，每一帧深度图像对应的点云模型是在相机的局部三维坐标系中。因此，不同的相机位置（即不同帧）便对应着不同的局部三维坐标系（local space frame）. 然后，重建后的模型需要坐落在一个坐标系，即世界坐标系或全局坐标系（world space frame）。于是，我们需要找到每一帧的相机局部坐标系同世界坐标系的位置关系，也就是确定每一帧中相机在世界坐标系中的位置。在计算机视觉和智能机器人领域，这个问题是经典的“同步定位与地图构建”中的定位问题：机器人在未知环境中，如何通过获取的周围环境的数据来确定自己所在的位置。

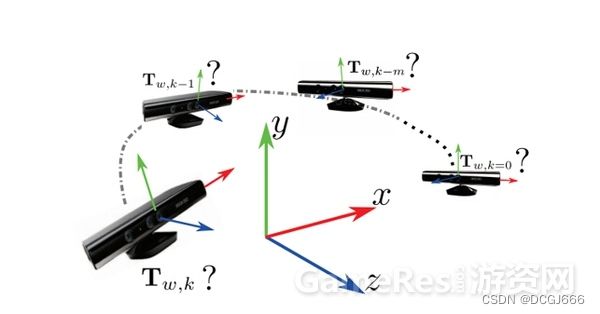
相机位置的估计
给定每一帧输入的RGBD数据，我们需要估计相机在世界坐标系中的位置。通常我们会把第一帧的相机位置当做是世界坐标系的原点，于是，我们需要估计的便是相机在此后每一帧相对于第一帧的位置的转移矩阵（transformation matrix）。使用数学语言描述是：在给定了第k-1帧重建的模型以及转移矩阵Tw,(k-1),还有第k帧的输入RGBD数据，估计出第k帧的转移矩阵Tw,k。这里的w下标指代世界坐标系world，k是帧的编号，k>1.

Newcombe等人于2011年提出的三维重建的经典方法KinectFusion 使用了迭代最近点（ICP）方法来解决以上问题。给定输入的原始数据（source）和目标数据（target），以及两者的数据点之间的对应关系，ICP计算得到原始数据和目标数据之间的转移矩阵，
该矩阵使得所有的目标数据点到其对应的原始数据点所在的切平面的距离之和最小。使用数学公式这个目标函数是：
$$E(T_{w,k})=\sum _i||T_{w,k}{s}_i-d_i|{|}_2^2$$
这里的si和di是原始数据点和对应的目标数据点，ni是si所在的切平面的法向量

为了给ICP算法找到合适的对应点，KinectFusion方法简单的将目标数据点——第k帧的数据点——通过转移矩阵Tw,k-1投影到原始数据点——第k-1帧的点，然后将两者作为对应相互对应的点。依照这种对应关系的ICP算法的最大优点是速度快，并且在扫描帧率相机的局部坐标系的数据中，便可得到在全局坐标系中的数据。

KinectFusion中的ICP方法仅仅使用了三维空间中的数据，并未考虑到RGB数据信息。另外，ICP必须要建立在扫描帧率较大，相邻两帧差别很小的前提下。因此，这种估计相机位置的方法存在较大的局限性，尤其是对存在较大平面的场景（如墙面，天花板和地板等）时，这种估计方法会带来很大的误差。KinectFusion之后的科研工作者们也提出了一些改进方法。例如，在估计相机位置时，同时考虑RGB信息和三维信息，并建立新的目标函数来进行优化。另外，使用已定义好的模型来模拟代替较大平面的物体，可以很好的排除掉这类物体所带来的扰动。

从大数据中建立模型
从上文可以看出，在估计了相机位置后，我们需要把新一帧第k帧的数据同已有的第k-1帧的模型数据结合起来，以输出优化后的模型。这其实就是本文在前面介绍的问题：对于每个现实场景中的点，如何从该点的众多“测量值”位置中估计出最终位置？

这个继续讲述经典的KinectFusion中所采用的方法。KinectFusion在世界坐标系中定义了一个立方体，并把该立方体按照一定的分辨率切割成小立方体（voxel）。图中定义了一个3x3x3米的立方体，并把立方体分为不同分辨率的小立方体网络。也就是说，这个大立方体限制了经过扫描重建的模型的体积。然后，KinectFusion使用了一种称为“截断有符号距离函数（TSDF）”的方法来更新每个小网络中的一个数值，该数值代表了该网格到模型表面的最近距离，也称为TSDF值。对于每个网格，在每一帧都会更新并记录TSDF到模型表面的最近距离，也称为TSDF值。对于每个网格，在每一帧都会更新并记录TSDF的值，然后再通过TSDF值还原出重建模型。例如，通过图8下两幅图中的网格的TSDF数值分布，我们可以很快还原出模型表面的形状和位置。这种方法通常被称为基于体数据的方法。该方法的核心思想是，通过不断更新并“融合”TSDF这种类型的测量值，我们能够越来越接近所需要的真实值。

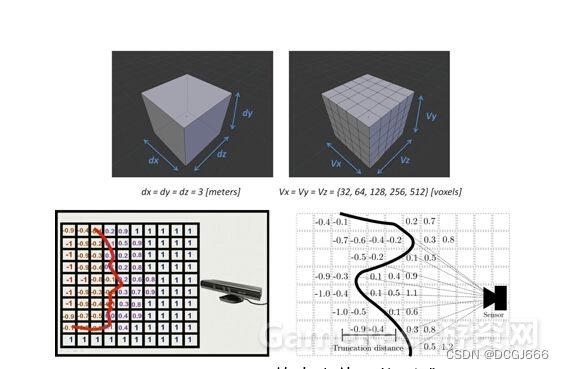
KinectFusion中TSDF的更新方法核心思想就是简单的对所有的测量值加权平均的过程。这种更新方式效率高，对于保证实时三维重建非常有必要。基于体数据的方法简单直观，而且容易使用并行计算实现，因此可以极大的增加扫描和重建效率。另外，使用计算机图形学中的网格生成相关方法，我们可以很容易从这种体数据的结果中生成三角网格模型，这对于进一步的研究和渲染非常重要。不过，这种方法也有很大缺点。例如，KinectFusion这种基于体数据的方法提前已经限定了扫描空间，超过这个空间的显示场景的物体将无法重建，这是因为定义立方体和网格需要的内存空间非常大。另外，立方体中的所有网格中的TSDF都需要记录，即便这个网格在现实场景中根本没有点，这就造成了极大的内存空间的浪费，并限制了扫描范围。这就意味着，KinectFusion之后的科研工作者们也提出了一些改进方法。例如，一种移动式的体数据网格方法可以不断移动定义好的网络模型到新的场景中，并不断输出已经重建好的模型到本地空间中，从而能够无限扩展扫描空间。另外，一些重建方法使用了点云的数据结构来代替体数据结构，在重建过程中不断把密集的点云数据融合成一定密度的点云。这种方式不要存储场景中的并不存在的点，因此能够节省大量空间以扩大扫描范围。