机器学习(六)：朴素贝叶斯及拉普拉斯修正

一.前言

2022年的第一篇博客，《机器学习》这个专栏去年由于自己的时间原因，更新的不勤，乘最近稍微有点时间准备开始陆陆续续更新，今天先来一道开胃菜：带拉普拉斯修正的朴素贝叶斯，话不多说请看下文。

二.贝叶斯定理

在正式介绍朴素贝叶斯算法之前先介绍下与其息息相关的贝叶斯定理（参考维基百科），其数学形式如下所示：
$$P(A|B)=\frac{P(A)P(B|A)}{P(B)}$$
在贝叶斯定理中:

• $P(A|B)$是已知$B$发生后，$A$的条件概率，也称为$A$的后验概率；
• $P(A)$是$A$的先验概率，其不考虑$B$方面的因素；
• $P(B|A)$是已知$A$发生后，$B$的条件概率，也称为$B$的后验概率；
• $P(B)$是$B$的先验概率。

先验概率是一开始由统计得到的客观概率，后验概率是在考虑和给出相关证据或数据后所得到的条件概率。

三.算法详解

3.1 贝叶斯决策

已知一个机器学习相关的分类问题共包含$N$个类别，即$\mathcal{Y}=\{c_1,c_2,...,c_N\}$，${\lambda }_{ij}$表示将一个真实标记为$c_j$的样本误分类为$c_i$所产生的损失。对于样本$\mathbf{x}$，基于后验概率$P(c_i|\mathbf{x})$可以得到将样本$\mathbf{x}$归到$c_i$类所产生的期望损失（也称为风险），即样本$\mathbf{x}$上的条件风险：
$$R(c_i|\mathbf{x})=\sum _{j=1}^N{\lambda }_{ij}P(c_j|\mathbf{x})\text{\hspace{1em}(1)}$$
公式（1）描述的是将样本$\mathbf{x}$归为类$c_i$需要冒多大的风险。

我们期望能够学得一个分类准则$h:\mathcal{X}\to \mathcal{Y}$，使得对样本空间所有样本的分类总体风险最小。显然，若选择的分类准则能使得每个样本的分类风险最小，那么总体风险也将被最小化。即对于每个样本，我们选择那个能使得条件风险的最小的类别标记：
$$h^{\ast }(\mathbf{x})={\text{arg min}}_{c\in \mathcal{Y}}R(c|\mathbf{x})\text{\hspace{1em}(2)}$$
令误判损失${\lambda }_{ij}$为：
$${\lambda }_{ij}=\{\begin{array}{l}0,\text{if}i=j\\ 1,\text{otherwise}\end{array}\text{\hspace{1em}(3)}$$
则将样本$\mathbf{x}$归类为$c_i,(i=1,2,...,N)$的风险可以表示为：
$$R(c_i|\mathbf{x})=\sum _{j\in S}P(c_j|x)\text{\hspace{1em}(4)}$$
其中$S=\{1,2,...,N\}-\{i\}$，由于将样本$\mathbf{x}$划分为各类的概率之和相加为1，因此式（4）也可以用表达式为：
$$R(c_i|\mathbf{x})=1-P(c_i|\mathbf{x})\text{\hspace{1em}(5)}$$
因此，欲最小化当前样本的风险只需要取使得后验概率$P(c_i|\mathbf{x})$最大的类别$c_i$。

那么问题的关键便是如何求取后验概率$P(c|\mathbf{x})$，实际上后验概率在现实任务中通常难以获取。因此，机器学习算法的目标便是基于有限的样本集尽可能准确地估计后验概率$P(c|\mathbf{x})$，一种常见的方法是利用贝叶斯定理，即：
$$P(c|\mathbf{x})=\frac{P(c)P(\mathbf{x},c)}{P(\mathbf{x})}\text{\hspace{1em}(6)}$$
对于给定的样本$\mathbf{x}$，$P(\mathbf{x})$对于所有类标记均相同，因此估计$P(c|\mathbf{x})$进一步转化为了基于训练数据$D$来估计先验概率$P(c)$和后验概率$P(\mathbf{x}|c)$：

• 类先验概率$P(c)$ 表达了样本空间中各类样本所占的比例，一般通过各类样本出现的频率来进行估计。
• 类条件概率$P(\mathbf{x}|c)$涉及关于$\mathbf{x}$所有属性的联合概率，直接根据样本出现的频率来估计将会遇到严重的困难，例如假设样本有$d$个属性，每个属性仅仅有两个取值，那么样本空间中将有$2^d$中取值，但实际的样本集中很难全覆盖这些取值，这会导致某些取值在训练集中没有出现，直接使用频率来估计$P(\mathbf{x}|c)$显然不可行。

3.2 朴素贝叶斯

基于3.1节中的讨论，我们知道$P(\mathbf{x}|c)$的估计是非常困难的，为了避开这个障碍，朴素贝叶斯算法采用了属性条件独立假设：对已知类别，假设所有属性相互独立，即假设每个属性独立地对分类结果产生影响。

基于属性独立条件假设，$P(c|\mathbf{x})$可写为：
$$P(c|\mathbf{x})=\frac{P(c)P(\mathbf{x}|c)}{P(\mathbf{x})}=\frac{P(c)}{P(\mathbf{x})}\prod _{i=1}^{d}P(x_i|c)\text{\hspace{1em}(7)}$$
其中$d$表示样本的属性个数，$x_i$表示$\mathbf{x}$在第$i$个属性上的取值。由于$P(\mathbf{x})$都所有类标记都相同，因此贝叶斯判定准则可写为：
$$h_{nb}={\text{arg max}}_{c\in \mathcal{Y}}P(c)\prod _{i=1}^{d}P(x_i|c)\text{\hspace{1em}(8)}$$
式（8）表示朴素贝叶斯分类器的表达式。3.1节介绍过$P(c)$可以通过各类样本出现的频率来进行估计，即：
$$P(c)=\frac{|D_c|}{|D|}\text{\hspace{1em}(9)}$$
其中$D_c$表示训练集$D$中第$c$类样本组成的集合。

对$P(x_i|c)$的估计，需要分离散属性和连续属性两种情况来进行讨论。对于离散属性，其可估计为：
$$P(x_i|c)=\frac{|D_{c,x_i|}}{|D_c|}\text{\hspace{1em}(10)}$$
其中$D_{c,x_i}$表示**$D_c$中第$i$个属性上取值为$x_i$的样本组成的集合**。对于连续属性，可考虑概率密度函数，假定$P(x_i|c)\sim \mathcal{N}({\mu }_{c,i},{\sigma }_{c,i}^2)$，其中${\mu }_{c,i}$和 ${\sigma }_{c,i}^2$分别表示第$c$类样本第$i$个属性上的均值和方差，即：
$$p\left(x_i\mid c\right)=\frac{1}{\sqrt{2\pi }{\sigma }_{c,i}}\exp \left(-\frac{{\left(x_i-{\mu }_{c,i}\right)}^2}{2{\sigma }_{c,i}^2}\right)\text{\hspace{1em}(11)}$$

3.3 拉普拉斯修正

需要注意的是，若某个属性值在训练集中没有与某个类同时出现过，则直接基于式（10）进行会直接使得样本判断为该类别的概率为0，这显然不合理。为避免其它属性携带的信息被训练集中未出现的属性值“抹去”，在估计概率值是可以使用拉普拉斯修正进行平滑，其具体做法为：
$$\begin{array}{rl}& P(c)=\frac{|D_c|+1}{|D|+N}\\ & P(x_i|c)=\frac{|D_{c,x_i|+1}}{|D_c|+N_i}\end{array}$$
其中$N$表示类别总数，$N_i$表示所有样本第$i$个属性可能的取值数。拉普拉斯修正避免了训练样本不充分而导致概率估值为0的问题，且当训练集较大时，修正对概率的影响将趋于无。

四.具体实现

本文拟实现处理连续属性版本的朴素贝叶斯（更通用一点），并在UCA的葡萄酒数据集Wine上进行训练与测评。

4.1 数据集

葡萄酒数据集包含178个样本，也分为三类(1, 2, 3)，其中第一类包含59个样本，第二类包含71个样本，第三类包含48个样本，在该数据集中包含了三种酒13种不同成分的数量，该数据集的部分数据展示如下：

其中各属性的说明如下：

属性	属性描述
Wine	类别
Alcohol	酒精
Malic.acid	苹果酸
Ash	灰
Acl	灰分的碱度
Mg	镁
Phenols	总酚
Flavanoids	黄酮类化合物
Noflavanoid.phenols	非黄烷类酚类
Proanth	原花色素
Color.int	颜色强度
Hue	色调
OD	稀释葡萄酒的OD280/OD315
Proline	脯氨酸

从上图可以看出，Wine数据集各个属性的尺度差异巨大，因此需要将其转换为相同的尺度，本文采取的措施是数据集的特征值进行了Z-score标准化，即：
$$x^{\prime }=\frac{x-\mu }{\sigma }$$
其中$\mu$和$\sigma$分别表示每个维度的均值和标准差，其实现源码为：

def standardization(data):
    """
    z-score归一化,即（X-Mean）/(Standard deviation)
    """
    mu = np.mean(data, axis=0)
    sigma = np.std(data, axis=0)
    return (data - mu) / sigma

另外，由于Wine数据集较小，按照数据集划分的常规思路，我们划分训练集和测试集的比例为8:2，划分前需要对数据集进行打乱操作。

4.2 模型实现

基于第三节的内容实现的处理连续属性的朴素贝叶斯算法如下：

class naiveBayes():
    def __init__(self,):
        """
        cols: 标识样本属性是离散的还是连续的
            1: 离散属性
            0: 连续
        example: cols = [1,1,0,1]
        """
        pass

    def fit(self,x,y):
        """
        x: ndarray, (n_samples, n_features)
        y: ndarray, (n_samples, )
        """
        self.params = self.getMeanAndStd(x,y)

    def predict(self,x):
        """
        x: ndarray, (n_samples, n_features)
        """
        flag,probs = False,None
        for pc,mu_c,std_c in self.params:
            pxc = self.normal_distribution(x,mu_c,std_c)
            if not flag:
                flag = True
                probs = (pxc.prod(axis=1) * pc).reshape(-1,1)
            else:
                pxc = (pxc.prod(axis=1) * pc).reshape(-1,1)
                probs = np.hstack([probs, pxc])
        return np.argmax(probs, axis=1)

    def getMeanAndStd(self,x,y):
        """
        计算连续属性的均值和标准差,即计算正态分布的参数
        """
        params = []
        for c in np.unique(y):
            tx = x[y==c]
            params.append([np.sum(y == c) / y.shape[0], tx.mean(axis=0),tx.std(axis=0)])
        return params
    
    def normal_distribution(self,x,mu,sigma):
        """
        功能: 计算P(x|c)
        x: 样本属性,(n_samples, n_features)
        mu: 均值列表,(N,)
        sigma: 标准差,(N, )
        """
        return 1 / (np.sqrt(2 * np.pi) * sigma) * np.exp(-1 * np.power(x - mu, 2) / (2 * np.power(sigma,2)))

4.3 实验结果与分析

我们利用测试集来进行模型的训练，然后在测试集上进行测评，并与sklearn中的朴素贝叶斯模型的性能进行了对比，实现的源码如下：

def main():
    # 调用自己生成的模型
    nb_m = naiveBayes()
    train_x,train_y,test_x,test_y = loadWine()
    nb_m.fit(train_x,train_y)
    pred_y = nb_m.predict(test_x)
    # sklearn中的朴素贝叶斯模型
    nb_sk = GaussianNB()
    nb_sk.fit(train_x,train_y)
    pred_y1 = nb_sk.predict(test_x)
    print("Sklearn Model Acc: {:.4f}, Our Model Acc: {:.4f}".format(
        accuracy_score(pred_y1, test_y),
        accuracy_score(pred_y, test_y)
    ))

# Sklearn Model Acc: 0.9722, Our Model Acc: 0.9722

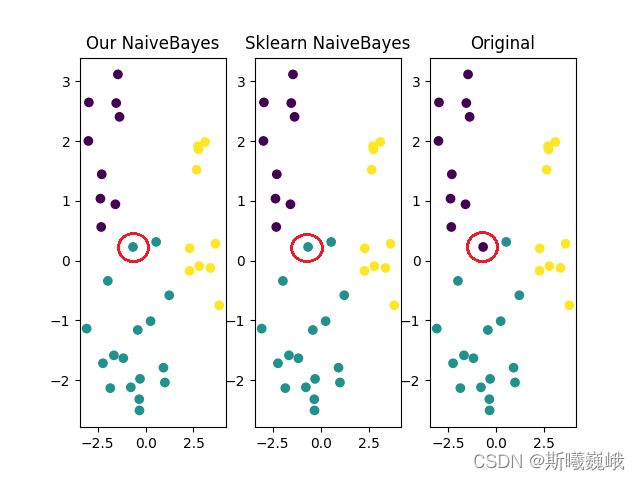
最后，我们对该数据集进行的降维可视化，对应的结果如下：

图中用红色圈圈圈出来的点是数据集中唯一分类错误的点。

五.结语

本文的源码已经在CSDN上传了，有条件的小伙伴支持一下博主（不贵），完整项目：naiveBayes

参考资料

• 《机器学习》周志华

以上便是本文的全部内容，要是觉得不错的话就点个赞或关注一下博主吧，你们的支持是博主继续创作的不解动力，当然若是有任何问题也敬请批评指正！！！