朴素贝叶斯原理详解(Navie Bayes)
朴素贝叶斯原理详解
- 1.知识准备
- 2.贝叶斯定理
- 3.贝叶斯定理在分类中的应用
-
- 3.1条件独立
- 3.2特征取离散值的条件概率
- 3.3特征取连续值的条件概率
-
- 高斯贝叶斯分类器:
- 多项式贝叶斯分类器:
- 伯努利贝叶斯分类器:
- 4.条件概率的m估计
- 5.逻辑斯特回归与朴素贝叶斯的区别
- 6.API
1.知识准备
1.贝叶斯分类器要解决的问题:
已知某样本中各个属性的取值, 求其属于某label的概率
2.先验概率与后验概率
先验概率: 根据以往的经验或数据分析得到的概率P(X)
后验概率: 根据先验概率得到的是后验概率P(Y|X)
3.朴素贝叶斯:
思想: 对于给定的待分类样本, 通过学习到的模型计算后验概率分布, 即: 在此样本出现(X)的条件下各个label出现的概率, 将后验概率最大的类作为样本所属的类别, 后验概率根据贝叶斯定理计算.
“学习得到的模型”: 就把它理解为由训练集已知的那几个概率, 然后通过贝叶斯公式就可以求得后验概率. 所以模型就是贝叶斯公式. 这句话等看完了这篇博客再回头, 会发现它是对朴素贝叶斯算法的高度概括. 先暂时放下, 跟着文章往后走.
4.损失函数
估计跟逻辑斯特回归的损失函数相同, 只是没有通过极大似然估计更新权值这一说. 因为贝叶斯分类器是要假设属性之间相互独立的(后面会做详细的解释)
5.为什么属性独立性假设在实际情况中很难成立, 但朴素贝叶斯仍能取得较好的效果?
(1)对于分类任务来说, 只要各类别的条件概率排序正确, 无需精确概率值即可导致正确分类
(2)如果属性间依赖对所有类别影响相同, 或依赖关系的影响能相互抵消, 则属性条件独立性假设在降低计算开销的同时不会对性能产生负面影响
6.贝叶斯分类器的特点
(1)属性可以离散, 连续
(2)数学基础扎实, 分类效率稳定
(3)对缺失值和噪声不太敏感
(4)属性如果不相关, 分类效果很好; 如果相关, 分类效果不低于决策树
2.贝叶斯定理
2.1 概率的基本理论
(1)样本空间: 随机试验E所构成的集合称为E的样本空间,记为S={e},其中e为样本点


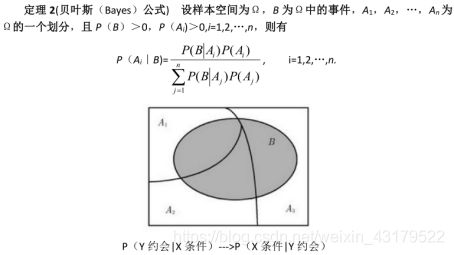
称上式为贝叶斯(Bayes)公式,也称为逆概率公式
全概率公式:
理论基础:P(AB)=P(B|A)*P(A)

全概率公式表明,在许多实际问题中,事件B的概率不易直接求得,如果容易找到Ω的一个划分,A1,A2…An,且P(Ai)和P(B|Ai)为已知,或容易知道,那么就可以根据全概率公式求出P(B)
通常在贝叶斯定理中使用全概率公式解决分母的问题.
用机器学习来解释贝叶斯公式:
特征集合X: 待测样本所有特征的集合(x1,x2…xn),特征的取值既可以是离散值也可以是连续值.
p(所属类别Y): 不同label取值在训练集中的概率
P(特征集合X): 训练集中与待测样本的特征集合X中各特征取值相同的样本在训练集的比例,一般通过全概率公式得到(不同label下的,与待测样本的特征集合X取值相同的样本在当前label中的比例,然后计算所有label下的比例之和)
p(特征集合X|所属类别Y): 训练集中所属类别为y且样本的特征取值与待测样本的特征取值X相同的所有样本与训练集中所属类别为Y的所有样本的比例
那么如何计算上面的公式?看下面
3.贝叶斯定理在分类中的应用
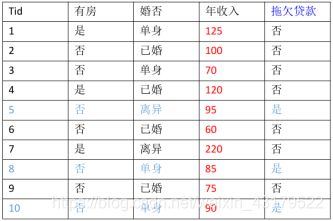
考虑任务: 预测一个贷款者是否会拖欠还款,我们基于以下图表做分析,假设有一样本X={有房=否,婚姻状况=已婚,年收入=120W},要分类该样本.我们需要利用训练数据中的可用信息计算后验概率P(Yes|X),P(No|X),如果P(Yes|X)>P(No|X),那么样本分类为Yes,否则No
(1)首先分析各维度数据的类型
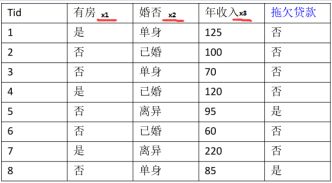
![]()
有房:二元变量, 婚否:分类变量,年收入:连续变量,拖欠贷款:类变量
准确估计label和属性值的每一种可能组合的后验概率非常困难,因为即便属性数目不是很大,仍然需要很大的训练集.此时,我们采用贝叶斯就比较方便,它允许我们使用先验概率P(Y),类条件概率P(X|Y)来表示后验概率:
![]()
上式中,分母P(X)通过全概率公式可计算得出,结果是常数,通常实践中可忽略.P(Y)先验概率可以通过计算训练集中属于每个类的训练记录所占的比例计算.所以现在需要求解的就只剩下P(X|Y), P(X|Y)的估计常用的有两种估计方法:朴素贝叶斯和贝叶斯网络.
(2)朴素贝叶斯分类
贝叶斯公式+条件独立假设 = 朴素贝叶斯方法
3.1条件独立
因为样本中各个特征都是独立的.所以:
![]()
条件独立假设等于说是用于分类的特征在类确定的条件下都是相互独立的,这一假设使得朴素贝叶斯算法变得简单,但是有时会牺牲一定的分类准确率(因为是从训练集得到的估计概率).
朴素贝叶斯分类时,对给定的输入样本x,通过学习到的模型计算后验概率分布P(Y=c|x),将后验概率最大的类作为样本x的类输出,后验概率计算根据上述的贝叶斯定理进行:

为什么用自己手机拍的照, 还自动加水印的, 我真的!!!
此时对P(X|Y = Ck)的类条件概率估计求解变为了对每个特征的类条件概率估计,即求:
P( X j X_{j} Xj = a j a_{j} aj | Y = C k C_{k} Ck)
而各个特征的取值既可以是离散值,也可以是连续值.所以要分别讨论.
&emsp ;以下求得的都是基于训练集的概率估计.
3.2特征取离散值的条件概率
对于特征 x i x_{i} xi,我们只需要根据类Y= C k C_{k} Ck中特征 x i x_{i} xi = a i =a_{i} =ai的训练实例的比例来估计特征的条件概率.
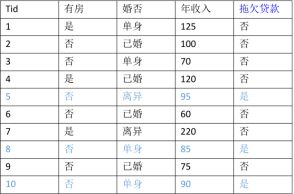
P( X j X_{j} Xj = a j a_{j} aj | Y = C k C_{k} Ck)
![]()
3.3特征取连续值的条件概率
高斯贝叶斯分类器:
P( X j X_{j} Xj = a j a_{j} aj | Y = C k C_{k} Ck): 特征的类条件概率服从正太分布
我们假设连续变量( X j X_{j} Xj)服从某种概率分布, 然后使用训练数据估计出分布的参数.那么特征取不同连续值时我们都可以知道此时特征的类条件概率,即P( X j X_{j} Xj = a j a_{j} aj | Y = C k C_{k} Ck)可求.
高斯分布被用来表示连续属性的类条件概率分布,如下表示每个类 C k C_{k} Ck,属性 x i x_{i} xi = a i =a_{i} =ai的类条件概率为:
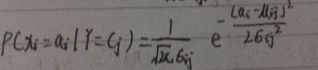
参数 μ i j μ_{ij} μij可以用类 y i y_{i} yi的所有训练记录关于 X i X_{i} Xi的样本均值 X ‾ \overline{X} X来估计, 参数 σ i j 2 σ^2_{ij} σij2可以用这些记录/样本的方差 s 2 s^2 s2来估计

注意如果采用了高斯贝叶斯分类器则说明对所有取连续值的特征的类条件概率都看成高斯分布的.(自己的理解)
多项式贝叶斯分类器:
特征的取值为离散值.
Multionmial:多项式贝叶斯分类器,假设特征的类条件概率分布满足多项式分布满足:

注意如果采用了多项式贝叶斯分类器则说明对所有取离散值的特征的类条件概率都看成多项式分布的.(自己的理解)
伯努利贝叶斯分类器:
特征的取值为二元的.
BernoulliNB是伯努利贝叶斯分类器,假设特征的类条件概率分布满足二项分布满足:
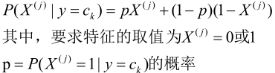
注意如果采用了伯努利贝叶斯分类器则说明对所有取离散值的特征的类条件概率都看成二项分布的.(自己的理解)
4.条件概率的m估计
针对的好像是取离散值的特征,取连续值的特征不会(很难)有类条件概率为0的情况.
问题: 如果有一个特征的类条件概率为0,则整个类的后验概率就变成0,仅使用训练集比例来估计类条件概率的方法对很多的场景是不够准确的,尤其在训练样本很少而属性数目很多的时候.
当一个或几个属性的类条件概率为0导致整个类的后验概率为0的时候,朴素贝叶斯就失效了,无法根据朴素贝叶斯来分类该记录.提出了m估计
m估计方法依照的数学公式为:
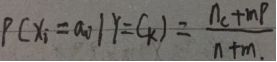
其中n为类别为 C k C_{k} Ck的样本数量, n c n_{c} nc为类别为 C k C_{k} Ck且 x i x_{i} xi取值为 a i a_{i} ai的样本数量, p为将要确定的先验概率估计(即P( X j X_{j} Xj = a j a_{j} aj | Y = C k C_{k} Ck)), m为等效样本的大小(常量,指定).
即p=( n c n_{c} nc+mp)/(n+m)
如何来理解这个公式:
首先, 先验的概率估计P( X j X_{j} Xj = a j a_{j} aj | Y = C k C_{k} Ck) = n c n_{c} nc / n
思考问题出现的根本原因:样本数量过小,所以为了避免这种情况,最好的方法就是等效的扩大样本的数量,即为观察样本(类别为 C k C_{k} Ck的样本)中添加m个等效的样本.此时:
类别为 C k C_{k} Ck的样本数量:n+m
类别为 C k C_{k} Ck且 x i x_{i} xi取值为 a i a_{i} ai的样本数量: n c n_{c} nc+mp
所以先验的概率估计P( X j X_{j} Xj = a j a_{j} aj | Y = C k C_{k} Ck) = ( n c n_{c} nc+mp)/(n+m)
5.逻辑斯特回归与朴素贝叶斯的区别
https://www.zhihu.com/question/265995680/answer/303148257
链接中对逻辑斯特回归与朴素贝叶斯回归的区别从数学上做了解释.
首先了解判别式模型与产生式模型
判别式模型与生成式模型
通过分析训练集,获得模型f(x),判别式模型与生成式模型就是两种通过训练集来获得最终的决策规则f(x)的基本思路.
判别式模型认为:获得y基于x的条件分布p(y|x)是关键.给定某个特定的x,对应的p(y|x)最大的y为决策的结果.因此,关键是找到p(y|x)的表达式.p(y|x)中包括若干个未知参数θ,因此p(y|x)也可以表示为p(y|x;θ).因此,需要通过训练集分析获得θ,然后进一步获得p(y|x;θ).机器学习采用极大似然估计的方法来确定未知参数,定义在训练集上的似然函数为:
![]()
机器学习的目标是选择特定的未知参数θ让这个似然函数最大化.在这个条件下,我们需要分析分布函数是p(y|x;θ),我们直接对这个分布函数的表现形式作假设.
我的理解:可以直接计算得到这个分布函数p(y|x;θ)
生成式模型认为:我们需要预测的决策结果y是事物的本质,而我们在做预测时拥有的可观察数据x为事物的表现,比如:y可以是”大象”,或者”猴子”,是本质.而x是我们看到的某个动物的特征,比如”吃草”,”生活在森林”等等.我们需要通过这些特征,来判断它究竟是什么动物.写到这里,就明白了,这实际上是一个贝叶斯判别的思路.本质上,是y决定了x!怎么理解呢?
我的理解:因为生成式模型认为y决定了x,所以p(x|y)可以直接计算得到,而p(y|x)不能直接计算得到.
从解决问题的思路上看,我们还是需要找到p(y|x),然后找到使得p(y|x)最大的那个y,但是因为是y决定了x而不是x决定y,所以我们不能直接对p(y|x)的分布形式进行假设(不能直接计算p(y|x)).此时就要用到贝叶斯公式.

因为我们可对p(x|y)和p(y)的概率分布作假设()直接计算.我们令p(x|y)=p(x|y;α),p(y)=p(y;β),α,β是待估计参数,这样就依然可以用极大似然估计的方法对α,β进行估计,极大似然函数表示为:
![]()
综上所述,获得决策变量y的根本目的是找到p(y|x).判别式模型直接对p(y|x)表现形式做假设,因为它认为是x决定了y,而生成式模型恰恰相反,认为是y决定了x,因此不能直接对p(y|x)的形式进行假设.所以需要借助于贝叶斯公式进行分析,最终对未知参数进行估计时都转化为对极大似然函数的优化问题进行求解.
特点:
判别式模型:寻找不同类别之间的最优分类面,反映的是异类数据之间的差异.
生成式模型:从统计的角度表示数据的分布情况,能够反映同类数据本身的相似度,不关心判别边界.
区别:
生成式模型(Generative Model)与判别式模型(Discrimitive Model)它们的区别在于:
假设有样本输入值(或者观察值)x,类别标签(或者输出值)y
判别式模型评估对象是最大化条件概率p(y|x)并直接对其进行建模.
生成式模型评估对象是最大化联合概率p(x,y)并对其建模
我对联合概率p(x,y)的理解:*p(x,y)=p(x|y)p(y).
其实两者的评估目标都是要得到最终的类别标签y,而y=argmaxp(y|x),不同的是判别式模型直接通过解在满足训练样本分布下最优化问题得到模型参数,主要用到拉格朗日乘算法,梯度下降法,常见的判别式模型如最大熵模型,CRF,LR,SVM
而生成式模型先经过贝叶斯转换成y=argmax p(y|x)=argmax p(x|y)*p(y),然后分别学习 p(x|y),p(y)的概率分布,主要通过极大似然估计的方法学习参数,如NGram,HMM,Naive Bayes
优缺点:
判别式模型:
优点:
1 分类边界更灵活,比使用纯概率方法或生成式模型得到的更高级
2 准确率往往较生成模型高
3 不需要求解类别条件概率,所以允许我们对输入进行抽象(比如降维,构造等),从而能够简化学习问题.
缺点:
1 不能反映训练数据本身的特性
生成式模型:
优点:
1 实际上带的信息比判别式模型丰富,研究单类问题比判别式模型灵活性强
2 模型可通过增量学习得到
3 生成式模型能够应付存在隐变量的情况,比如混合高斯模型就是含有隐变量的生成方法.
缺点:
1 学习过程比较复杂
2 实践中多数情况下判别式模型效果更好
常见的判别式模型:
Logistic Regression
SVM
Traditional Neural Networks
Nearest Neighbor
CRF
Linear Discriminant Analysis
Boosting
Linear Regression
常见的生成式模型:
Gaussians
Navies Bayes
Mixtures of Gaussians
Mixture of Experts
HMMs
Sigmoidal Belief Networks
Bayesian Networks
Markov Random Fields
Latent Dirichlet Allocation
经典提问:Navies Bayes与Logistic回归的区别是什么
1 前者是生成式模型,后者是判别式模型,二者的区别就是生成式模型与判别式模型的区别.
2 朴素贝叶斯方法是假设条件独立的,因为条件独立假设,朴素贝叶斯可以不使用梯度下降,而直接通过统计每个特征的逻辑发生比当做权值
而逻辑斯特回归,条件独立假设并不成立,通过梯度下降法,可以得到特征之间的耦合信息,从而得到相应的权值.
对上述表述所涉及的相关链接:
https://zhuanlan.zhihu.com/p/23103686
https://blog.csdn.net/Yaphat/article/details/52574748
https://blog.csdn.net/wolenski/article/details/7985426
https://blog.csdn.net/qq_34896915/article/details/75040686
https://www.zhihu.com/question/265995680
6.API
下面的API都是使用的是sklearn库中的
高斯贝叶斯分类器
GassianNB是高斯贝叶斯分类器,它假设特征的条件概率分布满足高斯分布(正太分布)
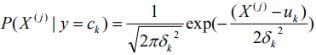
python中的sklearn中的原型为:
class sklearn.naive_bayes.GassianNB, GassianNB方法中没有参数, 无需调参
属性:
Class_propr_:一个数组,表示每个类别的概率P(y= c k c_{k} ck)
Class_count_:一个数组.表示每个类别包含训练样本的数量
Theta_:一个数组,每个类别上每个特征的均值 u k u_{k} uk
Sigma_:一个数组,每个类别上每个特征的标准差 δ k δ_{k} δk
方法:
fit(X,y):训练模型
Partial_fit(X,y):追加训练模型.该方法主要用于大规模数据集上的训练,此时可以将大数据集划分为若干个小数据集,然后在这些小数据集上连续调用partial_fit方法来训练模型
Predict(X):用模型进行预测,返回预测值
Predict_log_proba(X):返回一个数组,数组的元素依次是X(样本)预测为各个类别的概率的对数值(log值).
Predict_proba(X):返回一个数组,数组的元素一次是X(样本)预测为各个类别的概率
Score(X,y):返回在(X,y)上预测的准确率(accuracy)
多项式贝叶斯分类器
MultionmialNB是多项式贝叶斯分类器,它假设特征的条件概率分布满足多项式分布.
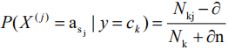

模型原型:
class sklearn.native_bayesMultionmialNB(alpha=1.0,fit_prior=True,class_prior=None)
参数:
alpha:一个浮点数,指定a值,也就是贝叶斯估计中的λ
Fit_prior:布尔值,如果为True则不去学习P(y= c k c_{k} ck),替代以均值分布,如果为False则去学习P(y= c k c_{k} ck).
Class_prior:一个数组,他指定了每个分类的先验概率(P= c k c_{k} ck),如果指定了该参数,则每个分类的先验概率不在从数据集中获取.
属性:
Class_log_propr_:一个数组,给出了每个类别先验概率分布的对数值.
Class_count_:一个数组,表示每个类别包含的训练样本数量
Feature_count_:一个数组,训练过程中,每个类别的特征遇到的样本数
Feature_log_prob_:一个数组对象,给出了P( X J X^J XJ|y= c k c_{k} ck)的先验概率分布的对数值
方法:
fit(X,y):训练模型
Partial_fit(X,y):追加训练模型,该方法主要用于大规模数据集上的训练,此时可以将大数据集划分为若干个小数据集,然后在这些小数据集上连续调用partial_fit()方法来训练模型.
Predict(X):用模型进行预测,返回预测值.
Predict_log_proba(X):返回一个数组,数组的元素依次是X预测为各个类别的概率的对数值
Predict_proba(X):返回一个数组,数组的元素一次是X预测为各个类别的概率
Score(X,y):返回在(X,y)上预测的准确率(accuracy)
伯努利贝叶斯分类器
BernoulliNB是伯努利贝叶斯分类器,它假设特征的条件概率分布满足二项分布:

模型原型:
class sklearn.native_bayes.BernoulliNB(alpha=1.0,brinarize=0.0,fit_prior=True,class_prior=None)
参数:
alpha:一个浮点数,指定a值,也就是贝叶斯估计中的λ
brinarize(二元化):一个浮点数或None
如果为None,那么会假设原始数据已经二元化
如果是浮点数,那么会以该数值为界,特征值大于的它的做1,特征值小于它的做0,采取这种策略来二元化.
Fit_prior:布尔值,如果为True则不去学习P(y= c k c_{k} ck),替代以均值分布,如果为False则去学习P(y= c k c_{k} ck).
Class_prior:一个数组,他指定了每个分类的先验概率(P= c k c_{k} ck),如果指定了该参数,则每个分类的先验概率不在从数据集中获取.
属性:
Class_log_propr_:一个数组,给出了每个类别先验概率分布的对数值.
Class_count_:一个数组,表示每个类别包含的训练样本数量
Feature_count_:一个数组,训练过程中,每个类别的特征遇到的样本数
Feature_log_prob_:一个数组对象,给出了P( X J X^J XJ|y c k c_{k} ck)的先验概率分布的对数值
方法:
fit(X,y):训练模型
Partial_fit(X,y):追加训练模型,该方法主要用于大规模数据集上的训练,此时可以将大数据集划分为若干个小数据集,然后在这些小数据集上连续调用partial_fit()方法来训练模型.
Predict(X):用模型进行预测,返回预测值.
Predict_log_proba(X):返回一个数组,数组的元素依次是X预测为各个类别的概率的对数值
Predict_proba(X):返回一个数组,数组的元素一次是X预测为各个类别的概率
Score(X,y):返回在(X,y)上预测的准确率(accuracy)