机器学习——多元线性回归算法预测房价
这是目录
- 一、Excel构造多元线性回归
- 二、Sklearn库重做多元线性回归
- 三、总结
- 参考文献
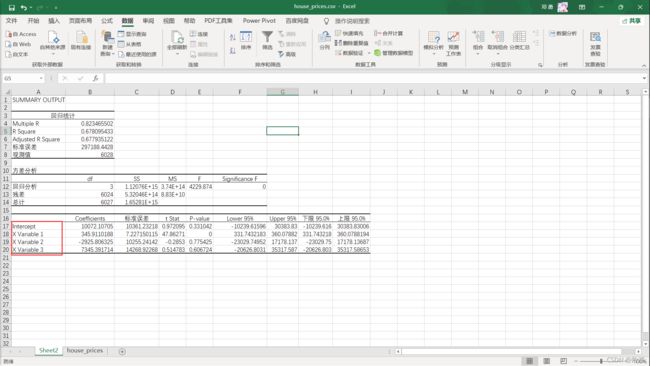
一、Excel构造多元线性回归
- 多元线性回归简介
在回归分析中,如果有两个或两个以上的自变量,就称为多元回归。事实上,一种现象常常是与多个因素相联系的,由多个自变量的最优组合共同来预测或估计因变量,比只用一个自变量进行预测或估计更有效,更符合实际。因此多元线性回归比一元线性回归的实用意义更大。
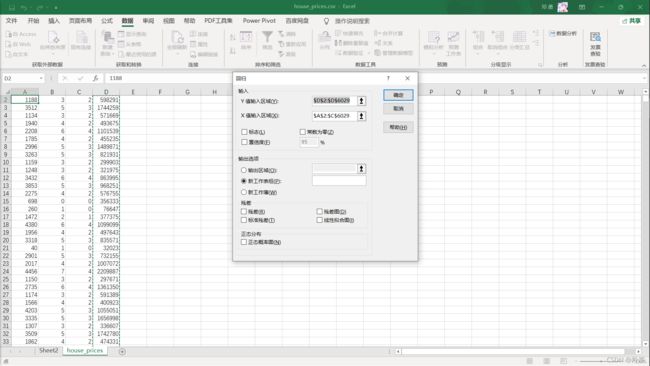
“garbage in garbage out”(简称GIGO),是计算机术语常用的俚语,意思是如果你输入错误的数据,那么输出的结果也是错误的。这个结论在机器学习领域也成立。多元线性回归属于监督机器学习算法,通过已知数据训练得到模型或决策函数。应用此算法时,不能盲目地套用算法,必须对数据的有效性、正确性、假设合理性进行验证,如果发现数据本身不正确,就需要纠正。 - 工欲善其事,必先利其器
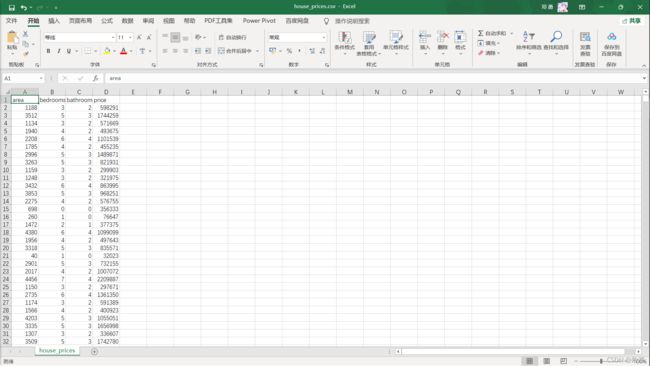
- 下载"多元线性回归模型预测房价.ipynb"与"house_prices.csv":
链接:https://pan.baidu.com/s/1gygRvofVtKkZUA_BsH399Q
提取码:m5nq- 利用Jupyter运行以上文件,并尝试理解
二、Sklearn库重做多元线性回归
- 导入包
import pandas as pd
import numpy as np
import seaborn as sns
from sklearn import datasets
from sklearn.linear_model import LinearRegression
- 读取文件
df = pd.read_csv('house_prices.csv')
df.info()#显示列名和数据类型类型
df.head(6)#显示前n行,n默认为5
- 取出自变量和因变量
#取出自变量
data_x=df[['area','bedrooms','bathrooms']]
data_y=df['price']
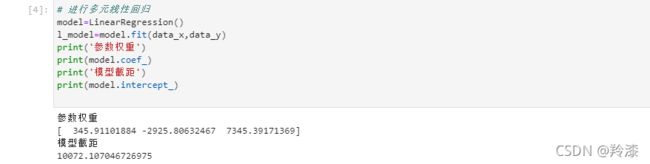
- 进行多元线性回归并得出结果
# 进行多元线性回归
model=LinearRegression()
l_model=model.fit(data_x,data_y)
print('参数权重')
print(model.coef_)
print('模型截距')
print(model.intercept_)
- 进行数据处理
# 异常值处理
# ================ 异常值检验函数:iqr & z分数 两种方法 =========================
def outlier_test(data, column, method=None, z=2):
""" 以某列为依据,使用 上下截断点法 检测异常值(索引) """
"""
full_data: 完整数据
column: full_data 中的指定行,格式 'x' 带引号
return 可选; outlier: 异常值数据框
upper: 上截断点; lower: 下截断点
method:检验异常值的方法(可选, 默认的 None 为上下截断点法),
选 Z 方法时,Z 默认为 2
"""
# ================== 上下截断点法检验异常值 ==============================
if method == None:
print(f'以 {column} 列为依据,使用 上下截断点法(iqr) 检测异常值...')
print('=' * 70)
# 四分位点;这里调用函数会存在异常
column_iqr = np.quantile(data[column], 0.75) - np.quantile(data[column], 0.25)
# 1,3 分位数
(q1, q3) = np.quantile(data[column], 0.25), np.quantile(data[column], 0.75)
# 计算上下截断点
upper, lower = (q3 + 1.5 * column_iqr), (q1 - 1.5 * column_iqr)
# 检测异常值
outlier = data[(data[column] <= lower) | (data[column] >= upper)]
print(f'第一分位数: {q1}, 第三分位数:{q3}, 四分位极差:{column_iqr}')
print(f"上截断点:{upper}, 下截断点:{lower}")
return outlier, upper, lower
# ===================== Z 分数检验异常值 ==========================
if method == 'z':
""" 以某列为依据,传入数据与希望分段的 z 分数点,返回异常值索引与所在数据框 """
"""
params
data: 完整数据
column: 指定的检测列
z: Z分位数, 默认为2,根据 z分数-正态曲线表,可知取左右两端的 2%,
根据您 z 分数的正负设置。也可以任意更改,知道任意顶端百分比的数据集合
"""
print(f'以 {column} 列为依据,使用 Z 分数法,z 分位数取 {z} 来检测异常值...')
print('=' * 70)
# 计算两个 Z 分数的数值点
mean, std = np.mean(data[column]), np.std(data[column])
upper, lower = (mean + z * std), (mean - z * std)
print(f"取 {z} 个 Z分数:大于 {upper} 或小于 {lower} 的即可被视为异常值。")
print('=' * 70)
# 检测异常值
outlier = data[(data[column] <= lower) | (data[column] >= upper)]
return outlier, upper, lower
- 得到异常集并进行丢弃
outlier, upper, lower = outlier_test(data=df, column='price', method='z')#获得异常数据
outlier.info(); outlier.sample(5)
df.drop(index=outlier.index, inplace=True)#丢弃异常数据
- 取出自变量和因变量
#取出自变量
data_x=df[['area','bedrooms','bathrooms']]
data_y=df['price']
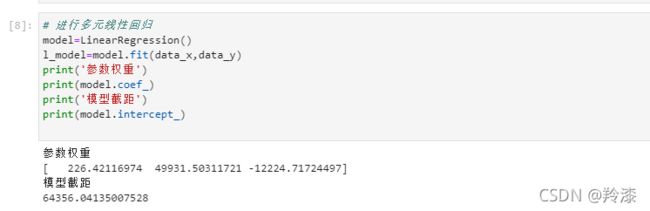
- 进行多元线性回归并得出结果
# 进行多元线性回归
model=LinearRegression()
l_model=model.fit(data_x,data_y)
print('参数权重')
print(model.coef_)
print('模型截距')
print(model.intercept_)
三、总结
初步了解了多元线性回归的步骤,也清楚了异常数据对于回归方程的影响,在进行数据处理之前应该先进行数据预处理,同时也要考虑两个变量的关系。
参考文献
多元线性回归分析