AIIC学习日记-CNN篇

AI

这部分主要是AI的学习记录。

吴恩达（DL部分）

记录一下，2019-11-x 初识CNN

吴恩达-神经网络和深度学习
由实验室的同学推荐，网易云课堂 吴恩达，第一次了解深度学习。

人类非常擅长理解非结构的物体，比如眼睛对图像的识别和耳朵对语音的识别，分别是二位和一维的处理。所以为什么不能很容易的理解一些高维的东西呢？

DL需要很多有标签的样本，而强化学习只需要规则，组合成DQN（用Q-learning产生标签，给deep-learning)。

训练CNN需要很大的算力，（数据样本很多），所以CPU吃力，GPU很勉强，ASIC成本太高，FPGA是一个不错的加速选择。

局限于认识CNN。

记录一下，2020-1-x 激活函数ReLu

记录一下，2020-2-1 神经网络有关名词

神经网络
又把卷积的概念和线性代数的矩阵相乘学了一遍。都忘了呀。relu，池化。（笔记在ipad上）

记录一下，2020-2-10 大体结构和历史

神经网络浅讲：从神经元到深度学习
主要是 ：矩阵乘法与线性代数之间的联系；以及隐藏层（在两层神经网络可以做非线性分类）对原始数据进行了空间变换，使得数据的原始坐标空间从线性不可分，转换成了线性可分。
输入层的节点数需要与特征的维度匹配，输出层的节点数要与目标的维度匹配。神经网络在用拟合函数的方式模拟大脑。输入如果是图像就是二维的，输出模拟大脑作识别应该是？维的。这句让我感觉到大脑的认知是一个固定的维度，如何改变这个固定的维度？很多未知的东西有更高的维度，很期待。

训练：机器学习模型训练的目的，就是使得参数尽可能的与真实的模型逼近。首先给所有参数赋上随机值。我们使用这些随机生成的参数值，来预测训练数据中的样本。样本的预测目标为yp，真实目标为y。那么，定义一个值损失(loss)，计算公式：loss=(yp * y)/2。

我们的目标就是使对所有训练数据的损失和尽可能的小。此时这个问题就被转化为一个优化问题：如何优化参数，能够让损失函数的值最小。一般来说解决这个优化问题使用的是梯度下降算法。梯度下降算法每次计算参数在当前的梯度，然后让参数向着梯度的反方向前进一段距离，不断重复，直到梯度接近零时截止。一般这个时候，所有的参数恰好达到使损失函数达到一个最低值的状态。eg:首先计算输出层的梯度，然后是第二个参数矩阵的梯度，接着是中间层的梯度，再然后是第一个参数矩阵的梯度，最后是输入层的梯度。计算结束以后，所要的两个参数矩阵的梯度就都有了。(很像强化学习Q-learning FPGA加速版本里，从目的节点开始往前传递（链式法则），逐渐收敛出一条最佳路径）

多层神经网络 ：A为神经元，W为参数。在相同层数下，增加神经单元能增加参数数量。如图（盗）从16增加到33。

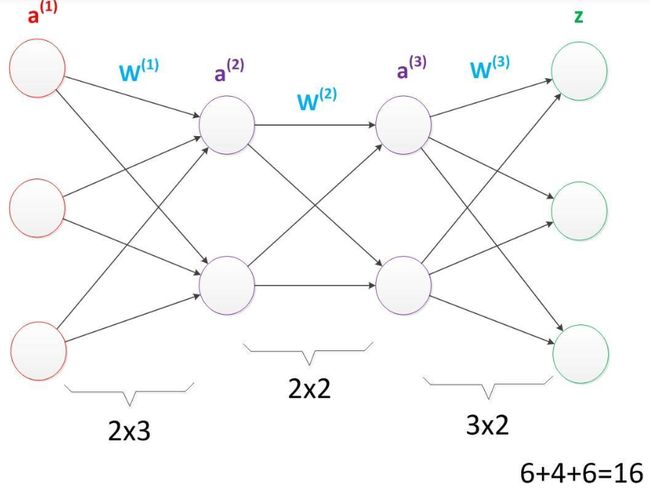
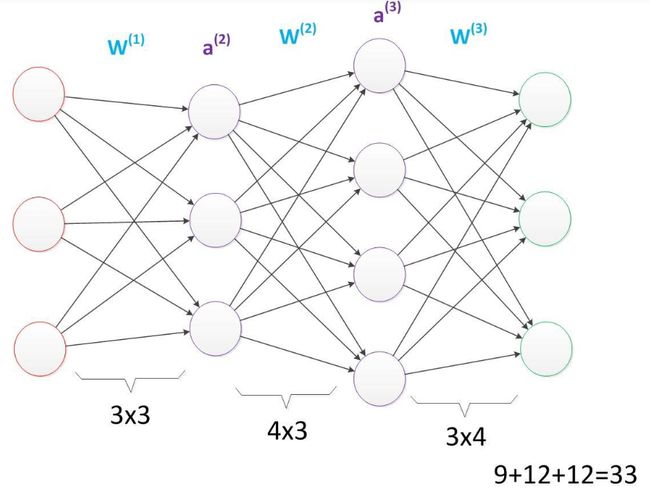
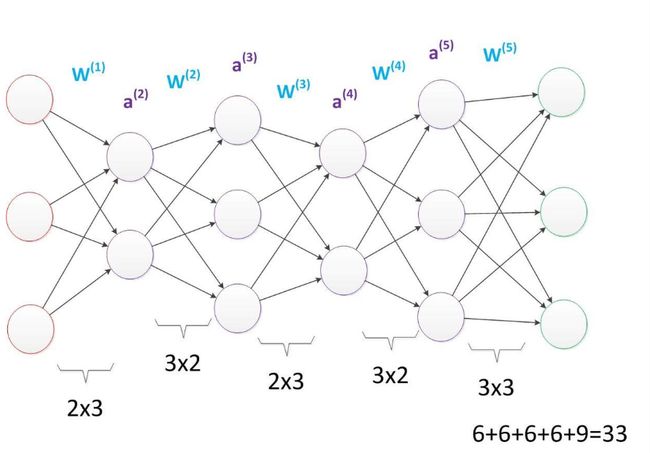
在参数相同的情况下，将每一层的神经元减少，增加为神经元的层数，可以提升神经网络的深度，以理解更深刻抽象的事物。

今天的学习就到这里了。事实上这个学习从很久之前就开始了，只是太懒了。

记录一下，2020-2-18 细节学习

吴恩达-神经网络和深度学习
1.logistic回归（二元回归）
输入标签：x特征向量（矩阵，表图像），输出标签：y表识别结果。
yi=σ（w^t*x+b）。yi为估计值，w和b为学习的参数。也可以看成判断的条件，决定输入的x为多少范围时才输出y=1(此处举例，1为识别结果）。

2.logistic训练的损失函数Loss
L(yi,y)=1/2(yi-y)^2 但梯度下降不一定能找到全局最优。yi为估计值，y为实际值。
L(yi,y)=-[ylogyi + (1-y)log(1-yi)] 凸优化：y=1时，L(yi,y)=-logyi,要求估计值yi足够大。 y=0时，L(yi,y)=log(1-yi),要求yi尽可能小->0。
loss function=J(w,b)=1/m*(Σ L(yi,y) ) (所有样本的求值后平均）

突然觉得这些公式又没有以前那么难了，可能是因为拆分学习了一部分。
3.梯度下降法
梯度下降指其能快速下降到中间的最低点，J(w,b)二维的如图1所示，这依赖于求导。

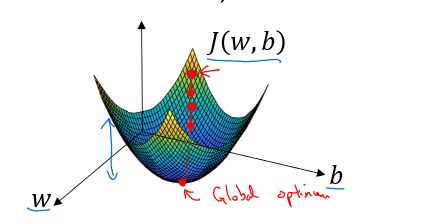
对于图二,w=w-α（dJ(w)/dw)
w很大的时候，偏导为正数，新的w=旧的w-aw导数，即向左边（中心，最低值）走一步。
w很小的时候，偏导为负数，新的w=旧的w-aw导数，即向右边（中心，最低值）走一步。
即向下降速度最快的地方走一步？？总之感觉在预习导数。无论如何觉得w=w-α（dJ(w)/dw)这个公式太妙了。能不断收敛直到中心/最小值。类似的，w=w+α（dJ(w)/dw)能收敛出中心/最大值。 这很像pid去适应目标。寻求最优。相比于Q-learning里的Qcs=R+γ*Qns，γ<1,最终收敛得到一个很大的值。
dvar在程序里表导数

4.求logistics回归里的梯度下降。（感觉吴老师讲的太好了）（非常有条理逻辑）
z代替了w^tx+b,a即yi表示估计（用了σ做激励函数），再由估计值a和实际值y求一个样本的Loss。

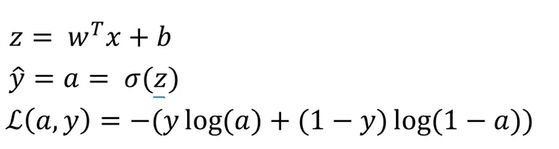
下图为变量关系图：

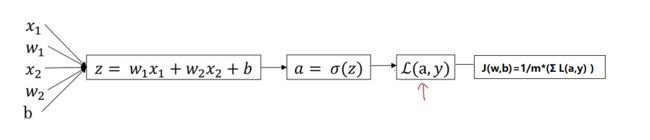
几个重要的式子：

da=δL(a,y) / δa;
dz=δL(a,y) / δz=a-y；
δL(a,y) / δw1=dw1=x1*dz;  db=dz;
dw=δJ / δw；

w=w-αdw;
b=b-αdb;

下面是求特征向量的流程，需要两个for循环（后面向量机会解决这个问题）
图中只求了一次梯度下降（一个for），每个梯度下降里需要对每个特征都计算一次。（感觉有3个for）仔细看其中的流程，有些陌生又十分地有意义，清晰明了。

5.向量化

1）通常的for写法

u = np.zeros((n,1)) #一列向量、矩阵
for i in rangge(n):
	u[i]=math.exp(v[i])

2）向量化写法，借助numpy。

import numpy as np
u = np.zeros((n,1)) #一列向量、矩阵
u=np.exp(v)

3）以下为logistics梯度下降做法，将多个w特征参数向量化为一维矩阵，即

dw = np.zeros((n-x,1))

dw += x[i]dz[i]

dw /= m

如下图中绿色部分，节省了for运算串行执行所需要的时间。

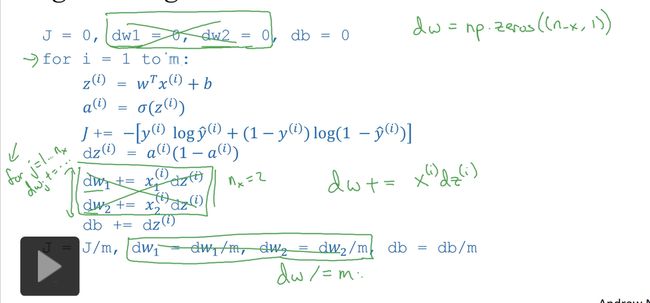
注意db的公式，z的公式。（python代码形式）
for语句只是m次迭代下降，每一次迭代里不需要for（而是向量化）

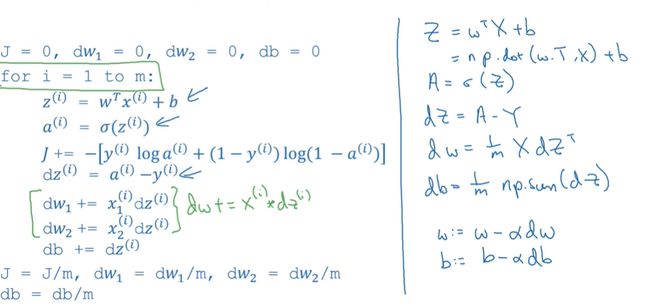
记录一下，2020-2-27

接上。
1.随机数初始化问题。
如果初始化的参数W，b一样，那么无论多少个样本去计算出来结果都相同。
w=np.random.rand( (2,2) ) *0.01; #把初值做很小，迭代会快（激活函数斜率大）

记录一下，2020-2-18

机器学习网站（入门、成长）

最近发现了几个比较好的网站，分享一下：

莫烦python 涵盖的内容比较系统、全面，适合新人。
机器学习基础有很多实战吧？
pytorch中文网站
吴恩达DL

记录一下，2020-7-3

最近做了一些AI加速的学习，回头看这篇文章，这篇文章在讲述的是AI的训练。而AI加速（我个人做的）是推断。

另外，卷积核=特征向量矩阵=目标物体的特征=本文中的w。