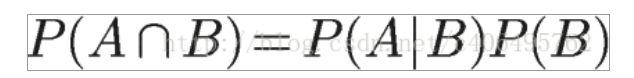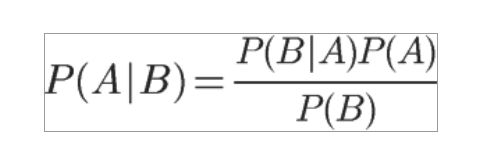Python之机器学习日记02——朴素贝叶斯01

机器学习日记02——朴素贝叶斯01

朴素贝叶斯基础篇

（参考资料：liukn教授机器学习教程，网络课程）

一、 前言

朴素贝叶斯算法是有监督的学习算法，解决的是分类问题，如客户是否流失、是否值得投资、信用等级评定等多分类问题。该算法的优点在于简单易懂、学习效率高、在某些领域的分类问题中能够与决策树、神经网络相媲美。但由于该算法以自变量之间的独立（条件特征独立）性和连续变量的正态性假设为前提，就会导致算法精度在某种程度上受影响。

本篇文章将从朴素贝叶斯推断原理开始讲起，通过实例进行辅助讲解。最后，使用 Python3 编程实现一个简单的言论过滤器。如果对于代码理解不够的，可以结合本文，观看由南京航空航天大学硕士：深度眸，为大家免费录制的视频：

（1） 概率论与数理统计精讲视频：http://pan.baidu.com/s/1qXRM5u0 密码：aio9
（2）朴素贝叶斯视频：http://pan.baidu.com/s/1kUJjoCv 密码：b2wr
（3）视频交流群：ML 与 DL 视频分享群(678455658)，欢迎提出宝贵意见。

二、朴素贝叶斯理论

朴素贝叶斯是贝叶斯决策理论的一部分，所以在讲述朴素贝叶斯之前有必要快速了解一下贝叶斯决策理论。

1. 贝叶斯决策理论

假设现在我们有一个数据集，它由两类数据组成，数据分布如下图所示：
我们现在用 p1(x,y)表示数据点(x,y)属于类别 1(图中红色圆点表示的类别)的概率，用 p2(x,y)表示数据点(x,y)属于类别 2(图中蓝色三角形表示的类别)的概率，那么对于一个新数据点(x,y)，可以用下面的规则来判断它的类别：
1.如果 p1(x,y) > p2(x,y)，那么类别为 1
2. 如果 p1(x,y) < p2(x,y)，那么类别为 2
也就是说，我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想，即选择具有最高概率的决策。已经了解了贝叶斯决策理论的核心思想，那么接下来，就是学习如何计算 p1 和 p2 概率。

2.条件概率

在学习计算 p1 和 p2 概率之前，我们需要了解什么是条件概率(Condittional probability)，就是指在事件 B 发生的情况下，事件 A 发生的概率，用 P(A|B)来表示。

根据文氏图，可以很清楚地看到在事件 B 发生的情况下，事件 A 发生的概率就是 P(A∩B)除以 P(B)。

因此，

同理可得，

所以，

即
这就是条件概率的计算公式。

3.全概率公式

除了条件概率以外，在计算 p1 和 p2 的时候，还要用到全概率公式，因此，这里继续推导全概率公式。

假定样本空间 S，是两个事件 A 与 A’的和。

上图中，红色部分是事件 A，绿色部分是事件 A’，它们共同构成了样本空间S。在这种情况下，事件 B 可以划分成两个部分。

在上一节的推导当中，我们已知

所以，

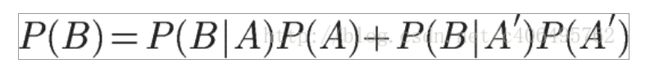
这就是全概率公式。它的含义是，如果 A 和 A’构成样本空间的一个划分，那么事件 B 的概率，就等于 A 和 A’的概率分别乘以 B 对这两个事件的条件概率之和。
将这个公式代入上一节的条件概率公式，就得到了条件概率的另一种写法：

4.贝叶斯推断

对条件概率公式进行变形，可以得到如下形式：

这就是贝叶斯推断的含义。我们先预估一个”先验概率”，然后加入实验结果，看这个实验到底是增强还是削弱了”先验概率”，由此得到更接近事实的”后验概率”。

在这里，如果”可能性函数”P(B|A)/P(B)>1，意味着”先验概率”被增强，事件 A的发生的可能性变大；如果”可能性数”=1，意味着 B 事件无助于判断事件 A 的可能性；如果”可能性函数”<1，意味着”先验概率”被削弱，事件 A 的可能性变小。

为了加深对贝叶斯推断的理解，我们一个例子。
两个一模一样的碗，一号碗有 30 颗水果糖和 10 颗巧克力糖，二号碗有水果糖和巧克力糖各 20 颗。现在随机选择一个碗，从中摸出一颗糖，发现是水果糖。请问这颗水果糖来自一号碗的概率有多大？

我们假定，H1 表示一号碗，H2 表示二号碗。由于这两个碗是一样的，所以P(H1)=P(H2)，也就是说，在取出水果糖之前，这两个碗被选中的概率相同。因此，P(H1)=0.5，我们把这个概率就叫做”先验概率”，即没有做实验之前，来自一号碗的概率是 0.5。再假定，E 表示水果糖，所以问题就变成了在已知 E 的情况下，来自一号碗的概率有多大，即求 P(H1|E)。我们把这个概率叫做”后验概率”，即在 E 事件发生之后，对 P(H1)的修正。根据条件概率公式，得到

这表明，来自一号碗的概率是 0.6。也就是说，取出水果糖之后，H1 事件的可能性得到了增强。

同时再思考一个问题，在使用该算法的时候，如果不需要知道具体的类别概率，即上面 P(H1|E)=0.6，只需要知道所属类别，即来自一号碗，我们有必要计算 P(E)这个全概率吗？要知道我们只需要比较 P(H1|E)和 P(H2|E)的大小，找到那个最大的概率就可以。既然如此，两者的分母都是相同的，那我们只需要比较分子即可。即比较 P(E|H1)P(H1)和 P(E|H2)P(H2)的大小，所以为了减少计算量，全概率公式在实际编程中可以不使用。

5.朴素贝叶斯推断

理解了贝叶斯推断，那么让我们继续看看朴素贝叶斯。贝叶斯和朴素贝叶斯的概念是不同的，区别就在于“朴素”二字，朴素贝叶斯对条件个概率分布做了条件独立性的假设。 比如下面的公式，假设有 n 个特征：

根据贝叶斯定理：

这就是贝叶斯分类器的基本方法：在统计资料的基础上，依据某些特征，计算各个类别的概率，从而实现分类。
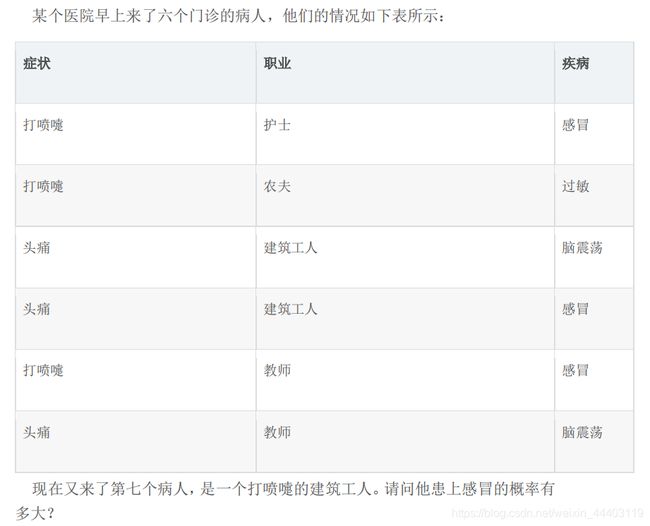
同样，在编程的时候，如果不需要求出所属类别的具体概率，P(打喷嚏) = 0.5和 P(建筑工人) = 0.33 的概率是可以不用求的。

三、动手实战

说了这么多，没点实践编程怎么行？以在线社区留言为例。为了不影响社区的发展，我们要屏蔽侮辱性的言论，所以要构建一个快速过滤器，如果某条留言使用了负面或者侮辱性的语言，那么就将该留言标志为内容不当。过滤这类内容是一个很常见的需求。对此问题建立两个类型：侮辱类和非侮辱类，使用1 和 0 分别表示。我们把文本看成单词向量或者词条向量，也就是说将句子转换为向量。考虑出现所有文档中的单词，再决定将哪些单词纳入词汇表或者说所要的词汇集合，然后必须要将每一篇文档转换为词汇表上的向量。简单起见，我们先假设已经将本文切分完毕，存放到列表中，并对词汇向量进行分类标注。编写代码如下：

#= -- coding: UTF-8 --
“”"
函数说明:创建实验样本

Parameters:
无
Returns:
postingList - 实验样本切分的词条
classVec - 类别标签向量
“”"

从运行结果可以看出，我们已经将 postingList 是存放词条列表中，classVec 是存放每个词条的所属类别，1 代表侮辱类 ，0 代表非侮辱类。

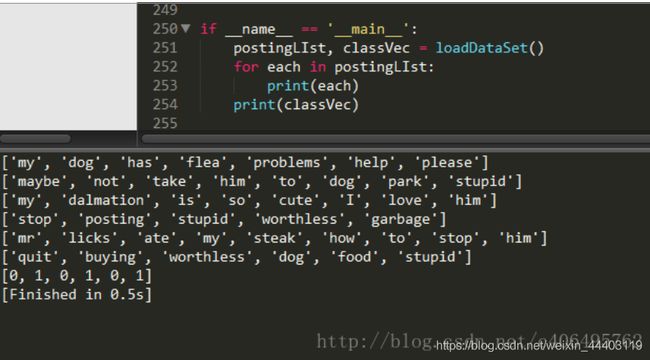
继续编写代码，前面我们已经说过我们要先创建一个词汇表，并将切分好的词条转换为词
条向量。

#= -- coding: UTF-8 --
“”"
函数说明:创建实验样本
Parameters:
无
Returns:
postingList - 实验样本切分的词条
classVec - 类别标签向量
“”"

从运行结果可以看出，postingList 是原始的词条列表，myVocabList 是词汇表。myVocabList是所有单词出现的集合，没有重复的元素。词汇表是用来干什么的？没错，它是用来将词条向量化的，一个单词在词汇表中出现过一次，那么就在相应位置记作 1，如果没有出现就在相应位置记作 0。trainMat 是所有的词条向量组成的列表。它里面存放的是根据 myVocabList向量化的词条向量。

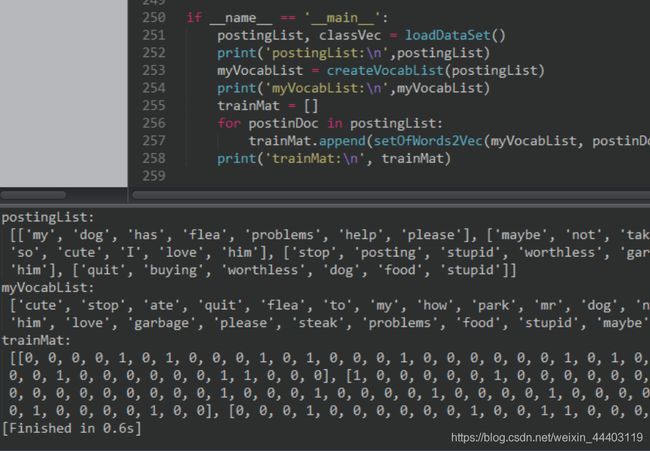
我们已经得到了词条向量。接下来，我们就可以通过词条向量训练朴素贝叶斯分类器。

“”"
函数说明:朴素贝叶斯分类器训练函数
Parameters:
trainMatrix - 训练文档矩阵，即 setOfWords2Vec 返回的 returnVec 构成的矩阵
trainCategory - 训练类别标签向量，即 loadDataSet 返回的 classVec
Returns:
p0Vect - 侮辱类的条件概率数组
p1Vect - 非侮辱类的条件概率数组
pAbusive - 文档属于侮辱类的概率
“”"

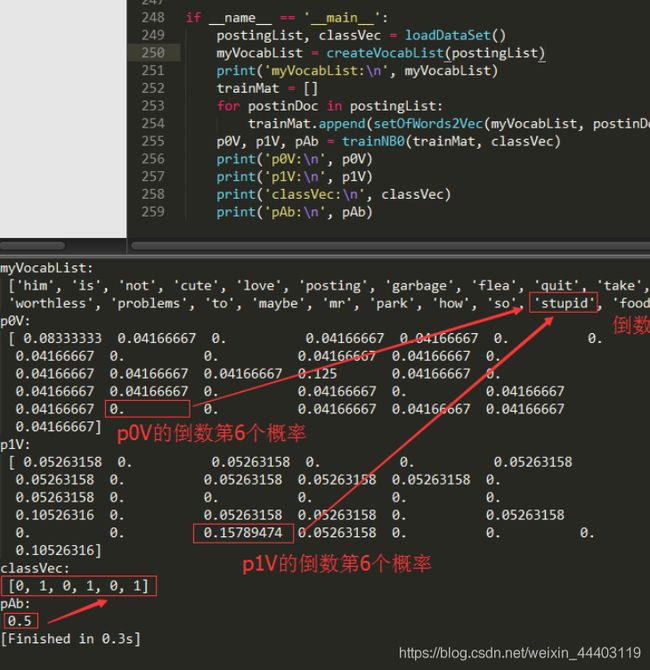
运行结果如下，p0V 存放的是每个单词属于类别 0，也就是非侮辱类词汇的概率。比如 p0V的倒数第 6 个概率，就是 stupid 这个单词属于非侮辱类的概率为 0。同理，p1V 的倒数第 6个概率，就是 stupid 这个单词属于侮辱类的概率为0.15789474，也就是约等于 15.79%的概率。我们知道 stupid 的中文意思是蠢货，难听点的叫法就是傻逼。显而易见，这个单词属于侮辱类。pAb 是所有侮辱类的样本占所有样本的概率，从 classVec 中可以看出，一用有 3 个侮辱类，3 个非侮辱类。所以侮辱类的概率是 0.5。因此 p0V 存放的就是 P(him|非侮辱类) = 0.0833、P(is|非侮辱类) = 0.0417，一直到 P(dog|非侮辱类) = 0.0417，这些单词的条件概率。同理，p1V 存放的就是各个单词属于侮辱类的条件概率。pAb 就是先验概率。

已经训练好分类器，接下来，使用分类器进行分类。

#= -- coding: UTF-8 --
import numpy as np
from functools import reduce
“”"
函数说明:创建实验样本
Parameters:
无
Returns:
postingList - 实验样本切分的词条
classVec - 类别标签向量
“”"

“”"
函数说明:根据 vocabList 词汇表，将 inputSet 向量化，向量的每个元素为 1 或 0
Parameters:
vocabList - createVocabList 返回的列表
inputSet - 切分的词条列表
Returns:
returnVec - 文档向量,词集模型
“”"

概率数组，属于非侮辱类的条件概率数组，文档属于侮辱类的概率
“”"
函数说明:朴素贝叶斯分类器分类函数
Parameters:
vec2Classify - 待分类的词条数组
p0Vec - 侮辱类的条件概率数组
p1Vec -非侮辱类的条件概率数组
pClass1 - 文档属于侮辱类的概率
Returns:
0 - 属于非侮辱类 1 - 属于侮辱类
“”"

“”"
函数说明:测试朴素贝叶斯分类器
Parameters: 无
Returns: 无
“”"

我们测试了两个词条，在使用分类器前，也需要对词条向量化，然后使用 classifyNB()函数，用朴素贝叶斯公式，计算词条向量属于侮辱类和非侮辱类的概率。运行结果如下：

你会发现，这样写的算法无法进行分类，p0 和 p1 的计算结果都是 0，这里显然存在问题。这是为什么呢？下一篇文章继续讲解~

四、总结

朴素贝叶斯推断的一些优点：
生成式模型，通过计算概率来进行分类，可以用来处理多分类问题。对小规模的数据表现很好，适合多分类任务，适合增量式训练，算法也比较简单。

朴素贝叶斯推断的一些缺点：
对输入数据的表达形式很敏感。由于朴素贝叶斯的“朴素”特点，所以会带来一些准确率上的损失。需要计算先验概率，分类决策存在错误率。

其它：
本文中的编程实例，只是简单的实例。存在一定的问题，需要进行改进，下篇文章会讲解改进方法；同时，本文中的编程实例，没有进行前期的文本切分，下一篇文章会讲解英文单词和中文单词的切分方法；

下篇文章将使用 sklearn 进行中文实例练习；
朴素贝叶斯的准确率，其实是比较依赖于训练语料的，机器学习算法就和纯洁的小孩一样，取决于其成长（训练）条件，”吃的是草挤的是奶，但不是所有的牛奶，都叫特仑苏”。

如有问题，请留言。如有错误，还望指正，谢谢！