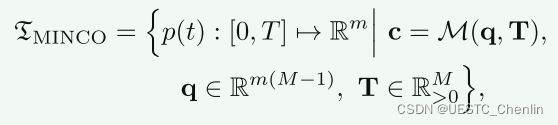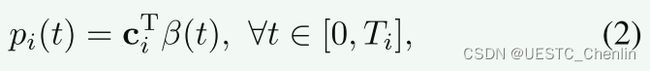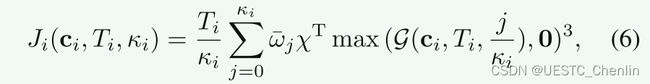【论文笔记】Decentralized Spatial-Temporal Trajectory Planning for Multicopter Swarms

摘要：分布式的多无人机群具有灵活性和鲁棒性，而有效的时空轨迹规划仍然是一个挑战。本文介绍了一种分布式时空轨迹规划方法，该方法将一种良好的MINCO轨迹表示方法引入到多Agent场景中。我们的方法确保每一个agent的高质量局部规划，无论是群体的协同还是杂乱环境中的安全要求。然后，将局部轨迹生成问题转化为无约束优化问题，在毫秒内得到有效求解。此外，还设计了一个分散异步机制来触发每个agent的本地规划。给出了一个系统的解决方案，带有工程考虑的详细描述。广泛的基准和室内/室外实验验证了其广泛的适用性和高质量。我们的源码将会发行，供社会参考。

1.引言

        与地面车辆或单机系统相比，空中群机器人能够进行三维操作（适应性，可扩展性和可维护性）和鲁棒性（可靠性，可持续性和可容错性）[4]。近年来，已经引起了大量的关注来开发先进架构和算法，去推动完全自主空中集群的边界。

        Swarm中的关键模块是其规划算法，它在编队飞行的效率和可行性中占据主导地位。调查最潜在的集群规划需求，不仅使轨迹的形状改变为避免碰撞，还可以调整时间曲线去开拓解空间，挖掘agent的可行性。空间-时间联合轨迹优化是实现这一目标的主要方法，但即使是单个智能体也具有挑战性。如果只执行空间变形 [26]，如图3所示，agent在通过一个狭窄的通道时，倾向于环航以等待其他agent，这阻碍了之后的agent并导致了劣质的解决方案。

图三：与/没有时间优化的轨迹比较。

虚线曲线：没有时间优化，agent使用绕道延迟时间。

实曲线：具有时间优化，产生更短，更光滑的轨迹。

为此，我们采用了最近开发的MINCO轨迹表示[24]，这是专门为积分器链系统的时空轨迹优化而设计的。此外，由于轨迹表示非常关键，但往往模棱两可，从MINCO开始，我们向机器人领域的开发人员介绍了几种常用的轨迹参数化方法（第II-A节）。

        基于MINCO，我们提出了一种能够对空中蜂群进行时空优化的分布式规划器。为了利用这种新的轨迹表示，设计了几个函数来惩罚碰撞、限制动力学不可行性或调整轨迹持续时间。利用MINCO的梯度传播方案，将罚函数在典型多项式轨迹上的梯度有效地传播到MINCO的梯度上。然后将规划问题作为无约束优化问题，能在几毫秒内快速求解。我们进一步将我们提出的算法部署到精心设计的硬件系统中。

        除了算法研究外，群体的另一个基本要求是架构，这需要适度的相互依赖，强大的通信机制和灵活的集群规模。此报告提供了分散和异步触发的规划策略，可降低问题的规模，并将计算负担分配给每个单个agent。还提出了将该系统带到现实世界的关键组件，例如相互的无人机检测，世界坐标系对齐，网络轨迹广播以及按需时间同步。最后，提出的完全自主群体系统是通过广泛的实验验证，如图1所示，富含障碍物，室内外环境的大量实验。如图1和2。

 

主要贡献如下：

1）一个分散的异步规划框架，它解耦了整个群规划问题，使系统对通信故障具有鲁棒性。

2）一种时空轨迹优化方法，将MINCO表示扩展到多智能体场景。

3）将完全自主的群体带到现实世界的工程实践。该软件将在我们的前作[24]接收后发布，供社区参考。

 2.相关工作

A.空中机器人的轨迹参数化

        表1总结了航空机器人典型轨迹参数化的优缺点。I.多项式 传统著作[12,13,17]广泛使用多项式曲线，他们主要使用多项式系数作为决策变量，以及显式连续性约束。许多著作[13,17]通过添加中间航路点waypoint来变形分段多项式轨迹。然而，航路点的分布需要仔细配置，以平衡可行性满意度和计算负担。为了优化多项式的时间分布，代表性方法使用带数值差的梯度下降[17]。然而，这种方法需要一个密集的矩阵求逆来将航路点转换为系数，这使得当问题规模扩大时，优化很快变得棘手。

      B’ezier和B样条具有凸包性质，这表明曲线完全包含在其控制点的凸包中[7,20]。因此，这些曲线便于添加约束，只需将控制点限制在可行凸区域内即可。许多作品[8,14,18]都遵循这一基本属性，并展示了在空中蜂群中的成功应用。然而，正如Tordesillas和How[19]所分析的那样，这一特性确实带来了保守性，防止了轨迹在其物理极限附近变得aggressive。此外，n阶B样条曲线自然是n− 1阶连续[6]。因此，只要B样条具有限定的阶数，就不需要连续性约束。对于B’ezier曲线，其时间分布可以通过它的基[7]以可接受的复杂度进行调整，而对于B样条曲线来说，这相当复杂，因为其时间评估包含高度非线性。

        MINCO[24]是一种新开发的轨迹表示法，专门用于积分链系统。MINCO的核心特点是，它能有效地处理各种各样的约束，同时保持空间和时间的最佳性。通过离散化轨迹以添加约束，MINCO不那么保守，但在得到解之后需要进一步检查。尽管MINCO是最复杂的表示，需要复杂的实现，但它为时空无人机群规划提供了坚实的基础。

B.分布式多旋翼集群

        对于分布式策略，VO（速度障碍）是一种生成无碰撞控制命令的轻量级方法[21,22]。然而，它不会产生具有高阶连续性的轨迹。因此，多旋翼机很难执行。Arul和Manocha[1]将VO作为速度约束纳入MPC，这显著提高了轨迹质量。此外，MPC广泛应用于航空群机器人的研究文献中。Van Parys和Pipleers[23]实现了对一组机器人的编队控制。Luis和Schoellig[10]使用分布式MPC执行点到点群变换。除此之外，Chen等人[3]通过逐步收紧碰撞约束，实现了非凸场景下多智能体轨迹规划的SCP。然而，上述方法需要在不同agent的Replan之间进行同步，这在现实世界中很难保证。为了进一步解耦系统，Liu等人[9]，Tordesillas和How[18]提出了无人机分散和异步规划策略，以避免静态/动态障碍物和机间碰撞。然而，上述基于优化的方法需要至少几十毫秒，甚至几秒钟来计算控制命令或轨迹。 更重要的是，这些算法仅通过仿真验证而没有集成传感，映射和定位。 McGuire等人显示了早期分布式的实验结果 [11]。然而，该论文中的天真的最小导航方法注定生成离散控制命令而没有考虑系统约束。最近，Zhou等人[26]构建了一个全自主多旋翼集群系统，利用

B样条对轨迹进行参数化。然而，当多个agent需要通过同一区域时，B样条曲线的时间调整困难会导致扭曲的轨迹形状。然而，我们提出的方法突破了这一限制。

3.集群的时空轨迹优化

A.总览

        时空轨迹优化的能力来自最近开发的轨迹表示，名为MINCO[24]。它的基本定义和特点将在第III-B，然后是III-C是关于如何向MINCO轨迹添加各种连续时间约束的一般描述：通过约束求积。最后是III-D，我们制定了一个无约束的非线性优化，然后用梯度下降法求解。为了以这种方式解决这个问题，各种目标的代价和梯度在III-D中定义和推导。

B.MINCO轨迹类

        由于四旋翼的微分平台特性，它们的运动规划足以直接在时间可微曲线上执行。在本报告中，我们采用MINCO[24]作为轨迹表示，这是一个最小控制多项式轨迹类，定义为

是m维M段多项式轨迹，多项式的阶数，s是相对积分器的阶数， 是多项式系数，是中间的航路点，是所有段的时间分配，所以，轨迹可以表示为

第i段轨迹由下式定义：

是基底，是系数矩阵，

 MINCO的核心是参数映射，由文献[24]的定义2推导。这个映射直接构建了最小控制轨迹对m维s阶积分链，适用于任何规定的初始和终端条件。图4直观地显示了MINCO中的一个实例。由于本报告侧重于集群规划，我们只直观地介绍了MINCO的特征。详细的证明见[24]。

图4： 展示了MINCO轨迹表示方式的参数和约束。轨迹由每个航点和时间直接参数化。红色点表示约束点（在III-C中引入），评估任何约束并传播到每个和 。 

特征1：MINCO由q和T紧凑地表示，是一类多项式轨迹，使得一下控制代价最小化：

 是一个拥有正数值的对角矩阵,是特定的起始和终止条件。是给定的中间航点，即轨迹在时间被强制通过的点。

特征2：映射矩阵的评估和导数有线性复杂度。一个更具体的对应关系可以表示为下面的函数，其中是一个非奇异性的带状矩阵，对于由文献[24]的定理2保证的任何一个T>0，。这两种轨迹表示(即 (c, T) 和 (q, T)) 之间的转换是利用具有O (M) 线性时间和空间复杂度的带状PLU分解来实现的。该评估非常快速，在桌面CPU上生成最小jerk轨迹需要每段轨迹大约1 μs。

特征3：特征2允许任何用户定义的目标函数或罚函数,MINCO对应的目标函数由下式计算：

 

 然后映射给出了一种线性复杂度的方式去计算和对应于和，然后，一个高级优化器就能有效的优化目标函数。

 C.时间积分限制

        各种约束的实现方式与轨迹参数化方法密切相关。通常，对动力学可行性和避碰的要求被表述为功能型约束。然而，由于G包含无限多个不等式约束，这种公式不能直接由约束优化处理。因此，我们通过约束违规的积分将G转换为有限维。实际上，积分被转换为采样惩罚函数的加权和。在大多数情况下，约束被解耦，即用的约束仅由Ci和Ti确定，将第i段轨迹的惩罚计算为

 

其中是第i段轨迹上的采样数，是惩罚权重向量，具有适当大的条目，=（1 / 2,1，····1,1 / 2）是梯形规则的正交系数[15]。我们定义由确定的点作为约束点˚PI，j = pi（（j /κi）ti）与pi（t）第i段多项式轨迹。然后g（ci，ti，j /κi）= g（˚pi，j）。注意˚pi，κi=˚pi1,0。在此处使用立方惩罚的两倍于持续可微分。然后将Jς（C，T）定义为求和：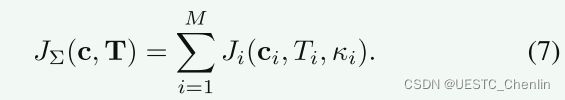 

因为

 

 从上述方程式中，一旦求出了相对于多项式系数CI和时间T的约束G的梯度，就可以有效地计算出的梯度。

 D.优化问题构建

        根据轨迹参数化的定义和强制约束，我们介绍了轨迹规划的完整优化方法。对期望轨迹的基本要求是平滑性、动力学可行性以及障碍物和agent之间的安全性。额外的目标还有，例如最小化控制工作量和执行时间。在这份报告中，我们采用MINCO来解决所有问题。由于定理2在 [24] 中自然保证了MINCO的光滑性，因此无需对轨迹连续性付出额外的工作。 

在这项工作中，我们将轨迹生成描述为一个无约束优化问题：

其中Jx是J∑实例，λx是目标或惩罚的权重，下标x={e，t，d，o，w，u}表示控制代价（e）、执行时间（t）、动力学可行性（d）、障碍回避（o）、群间避碰（w）和约束点的均匀分布（u）。通常情况下，足够大的重量足以承受处罚。该问题通过无约束非线性优化求解。

1）

2）

3）

4）

5）

6）

4.Benchmark

5.真实实验

6.总结与未来工作