Python----稀疏矩阵

稀疏矩阵：

• 零元素的个数远远多于非零元素

• 反义词：稠密矩阵

 

Scipy：

• 创建稀疏矩阵的工具
• 将稠密矩阵转化为稀疏矩阵的工具
• 可以在Scipy上运行的函数：
  • 许多在Numpy数组上运行的线性代数Numpy和SciPy函数
  • Numpy数据结构的机器学习库，如：机器学习的scikit-learning和用于深度学习的Keras

 

Scipy中有可以表示的7种稀疏矩阵类型：

1. csc_matrix: Compressed Sparse Column format(压缩稀疏列)
2. csr_matrix: Compressed Sparse Row format(压缩稀疏行)
3. bsr_matrix: Block Sparse Row format(块稀疏行)
4. lil_matrix: List of Lists format(列表的列表)
5. dok_matrix: Dictionary of Keys format(字典键值)
6. coo_matrix: COOrdinate format (aka IJV, triplet format)()(坐标)
7. dia_matrix: DIAgonal format()(对角)

• coo_matrix(坐标):

​​​​​​                          ​

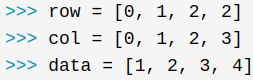
最简单的存储方式：三个数组row、col和data保存非零元素的行下标，列下标与值

coo_matrix主要用来创建矩阵

coo_matrix无法对矩阵的元素进行增删改等操作

一旦创建之后，除了将之转换成其它格式的矩阵，几乎无法对其做任何操作和矩阵运算

优点：

转换成其它存储格式很快捷简便，转换成csr/csc很快

允许重复的索引（例如在1行1列处存了值2.0，又在1行1列处存了值3.0，则转换成其它矩阵时就是2.0+3.0=5.0）

缺点：

不支持切片和算术运算操作

>>> row = [0, 1, 2, 2]
>>> col = [0, 1, 2, 3]
>>> data = [1, 2, 3, 4]
# 生成coo格式的矩阵
>>> coo_mat = sparse.coo_matrix((data, (row, col)), shape=(4, 4))
>>> coo_mat
<4x4 sparse matrix of type ''
    with 4 stored elements in COOrdinate format>

>>> coo_mat.toarray()
array([[1, 0, 0, 0],
       [0, 2, 0, 0],
       [0, 0, 3, 4],
       [0, 0, 0, 0]])

•  

• dok_matrix(和coo有点像, 只不过元祖是"键", data是"值"):

  • 逐渐添加矩阵的元素

  • 采用字典来记录矩阵中不为0的元素: 

    • key: 记录元素的位置信息的元祖

    • value: 记录元素的具体值

• 优点：
  • 递增的构建稀疏矩阵很高效
  • 访问某个单元，只需要O(1)
• 缺点：
  • 不允许重复索引（coo中适用），但可以很高效的转换成coo后进行重复索引

>>> S = sparse.dok_matrix((5, 5), dtype=np.float32)
>>> for i in range(5):
      for j in range(5):
        S[i,j] = i+j    # 更新元素

>>> S.toarray()
[[0. 1. 2. 3. 4.]
 [1. 2. 3. 4. 5.]
 [2. 3. 4. 5. 6.]
 [3. 4. 5. 6. 7.]
 [4. 5. 6. 7. 8.]]

 

• lil_matrix(两列表: 一个每行中的非0元素, 一个每个元素对应列):

• 用两个列表存储非0元素。

• data保存每行中的非零元素,rows保存非零元素所在的列。

• 适合逐个添加元素，并且能快速获取行相关的数据。

>>> l = sparse.lil_matrix((4, 4))
>>> l[1, 1] = 1
>>> l[1, 3] =2
>>> l[2, 3] = 3
>>> l.toarray()
array([[0., 0., 0., 0.],
       [0., 1., 0., 2.],
       [0., 0., 0., 3.],
       [0., 0., 0., 0.]])

•  优点：
  • 适合递增的构建成矩阵
  • 转换成其它存储方式很高效
  • 支持灵活的切片
• 缺点：
  • 当矩阵很大时，考虑用coo
  • 算术操作，列切片，矩阵向量内积操作慢

• csr_matrix:(列号, 数据, 第一个元素起始行+到该行结束有多少数据)

>>> data = np.array([1, 2, 3, 4, 5, 6])  #数据
>>> indices = np.array([0, 2, 2, 0, 1, 2])  #每个数据的列下标
>>> indptr = np.array([0, 2, 3, 6])  #0:起始的行号  2,3,6: 到该行累计有几个数

>>> csr_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 2],
       [0, 0, 3],
       [4, 5, 6]])

• csc_matrix:(列号, 数据, 第一个元素起始行+到该行结束有多少数据)

>>> data = np.array([1, 2, 3, 4, 5, 6])  #数据
>>> indices = np.array([0, 2, 2, 0, 1, 2])  #每个数据的行号
>>> indptr = np.array([0, 2, 3, 6])  #0:起始的列  2,3,6:到该列累计有多少数据

>>> csc_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 4],
       [0, 0, 5],
       [2, 3, 6]])

 

 

参考博文（写得非常好）：https://www.cnblogs.com/hellojamest/p/11769467.html

 

---

---

---

 

scipy.sparse.diags：从对角线构造稀疏矩阵：

scipy.sparse.diags(diagonals, offsets=0, shape=None, format=None, dtype=None)

• 参数：
  • diagonals：用来构成对角线的数组序列
  • offsets：对应的对角线
    • 0：主对角线
    • 1：主对角线上面的对角线
    • -1：主对角线下面的对角线
    • 2：主对角线上两个对角线
• 用已有的数组序列构造，并且标明分别属于哪个对角线

>>> from scipy.sparse import diags
>>> diagonals = [[1, 2, 3, 4], [1, 2, 3], [1, 2]]
>>> diags(diagonals, [0, -1, 2]).toarray()
array([[1, 0, 1, 0],
       [1, 2, 0, 2],
       [0, 2, 3, 0],
       [0, 0, 3, 4]])

>>> diags([1, 2, 3], 1).toarray()
array([[ 0.,  1.,  0.,  0.],
       [ 0.,  0.,  2.,  0.],
       [ 0.,  0.,  0.,  3.],
       [ 0.,  0.,  0.,  0.]])

• 用单个元素构造，并且表明分别属于哪个对角线和形状

>>> diags([1, -2, 1], [-1, 0, 1], shape=(4, 4)).toarray()
array([[-2.,  1.,  0.,  0.],
       [ 1., -2.,  1.,  0.],
       [ 0.,  1., -2.,  1.],
       [ 0.,  0.,  1., -2.]])

参考博文：https://blog.csdn.net/lonelykid96/article/details/102733088