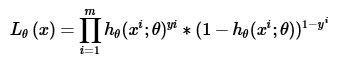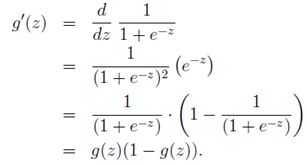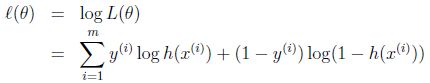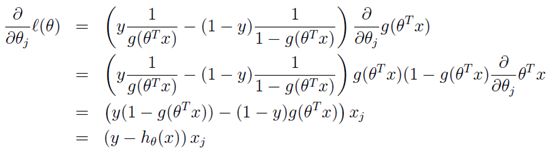简介~假设~损失(似然)~推导~梯度(全大慢,随局小减)
梯度~反向传播~实例~局部~凸函数
一、逻辑回归简介
一句话概括:逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法,运用梯度下降来求解参数,来达到将数据二分类的目的
这里面其实包含了5个点 1:逻辑回归的假设,2:逻辑回归的损失函数,3:逻辑回归的求解方法,4:逻辑回归的目的,5:逻辑回归如何分类。这些问题是考核你对逻辑回归的基本了解
- 逻辑回归的假设:
逻辑回归的第一个基本假设是假设数据服从伯努利分布。伯努利分布有一个简单的例子是抛硬币,抛中为正面的概率是p,抛中为负面的概率是1-p,逻辑回归需要将线性模型进行一下映射,从而能用于分类
这里的映射函数或者叫分类器叫做sigmoid函数,通过sigmoid函数分类器,逻辑回归的第二个假设是假设样本为正的概率是:
\( P(y=1|x;\theta ) = \frac{1}{1+e^{-z}} = \frac{1}{1+e^{-\theta^Tx}} \)
- 逻辑回归的损失函数:
常用的损失函数有以下几种:
-
- 0-1损失函数:
\(L(Y,f(X)) = \left\{\begin{matrix}1 & Y \neq f(X)\\ 0 & Y = f(X)\end{matrix}\right.\)
-
- 平方损失函数:
\(L(Y,f(X)) = (Y - f(X))^2\)
-
- 绝对损失函数:
\(L(Y,f(X)) = | Y - f(X))|\)
-
- 对数损失函数或对数似然损失函数:
\(L(Y,P(Y|X)) = -logP(Y|X)\)
对于逻辑回归模型,使用的是对数损失函数作为代价函数,则本例中,逻辑回归的损失函数为:
\(cost(y,p(y|x)) = \left\{\begin{matrix}-logp(y|x) & if(y = 1)\\ -log(1-p(y|x))& if(y = 0)\end{matrix}\right.\)
将上面的两个表达式合并,则得到单个数据点上的log损失为:
\(cost(y,p(y|x)) = -ylogp(y|x) - (1-y)log(1-p(y|x))\)
因为y只有两种取值情况,1或0,分别令y=1或y=0,即可得到原来的分段表达式,即两者是等价的。全体样本的损失函数则可表达为:
\(cost(y,p(y|x)) = \sum_{i=1}^{m} -y_ilogp(y_i|x_i) - (1-y_i)log(1-p(y_i|x_i))\)
其中\(p(y|x)\)由前面的逻辑回归模型定义,令:
\(p(y|x) = h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}\)
则最终的损失函数为:
\(cost(y,p(y|x)) = \sum_{i=1}^{m} (-y_ilog\frac{1}{1+e^{-\theta^Tx}} - (1-y_i)log(1-\frac{1}{1+e^{-\theta^Tx}}))\)
即逻辑回归的损失函数是它的极大似然函数:
- 逻辑回归的求解方法:
由于该极大似然函数无法直接求解,一般通过对该函数进行梯度下降来不断逼近最优解。因为就梯度下降本身来看的话就有随机梯度下降,批梯度下降,small batch 梯度下降三种方式
面试官可能会问这三种方式的优劣以及如何选择最合适的梯度下降方式
-
- 梯度下降会获得全局最优解(损失函数是凸函数),缺点是在更新每个参数的时候需要遍历所有的数据,计算量会很大,每个参数的更新都会很慢
- 随机梯度下降是以高方差频繁更新,优点是使得sgd会跳到新的和潜在更好的局部最优解,缺点是使得收敛到局部最优解的过程更加的复杂
- 小批量梯度下降每次更新的时候使用n个样本。减少了参数更新的次数,可以达到更加稳定收敛结果,一般在深度学习当中我们采用这种方法
-
- 其实这里还有一个隐藏的更加深的加分项,看你了不了解诸如Adam,动量法等优化方法。因为上述方法其实还有两个致命的问题
-
- 第一个是如何对模型选择合适的学习率。自始至终保持同样的学习率其实不太合适。因为一开始参数刚刚开始学习的时候,此时的参数和最优解隔的比较远,需要保持一个较大的学习率尽快逼近最优解。但是学习到后面的时候,参数和最优解已经隔的比较近了,你还保持最初的学习率,容易越过最优点,在最优点附近来回振荡,通俗一点说,就很容易学过头了,跑偏了
- 第二个是如何对参数选择合适的学习率。在实践中,对每个参数都保持的同样的学习率也是很不合理的。有些参数更新频繁,那么学习率可以适当小一点。有些参数更新缓慢,那么学习率就应该大一点
- 逻辑回归的目的:
将数据二分类,提高准确率
- 逻辑回归如何分类:
逻辑回归作为回归,如何应用到分类上去?y值确实是一个连续的变量。逻辑回归的做法是划定一个阈值,y值大于这个阈值的是一类,y值小于这个阈值的是另外一类。阈值具体如何调整根据实际情况选择。一般会选择0.5做为阈值来划分。
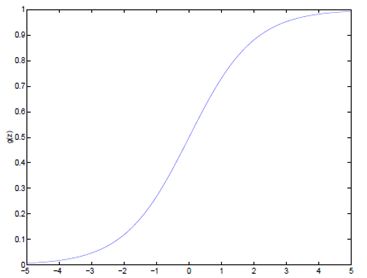
二、Sigmoid函数
如果我们忽略二分类问题中y的取值是一个离散的取值(0或1),我们继续使用线性回归来预测y的取值。这样做会导致y的取值并不为0或1。
逻辑回归使用一个函数来归一化y值,使y的取值在区间(0,1)内,这个函数称为Logistic函数(logistic function),也称为Sigmoid函数(sigmoid function)。函数公式如下:
\( g(z) = \frac{1}{1+e^{-z}} \)
函数图像如下:
该函数导数有一个特性:
经过Sigmoid函数转换后的y值有特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
\( P(y=1|x;\theta ) = h_\theta (x) \)
\( P(y=0|x;\theta ) = 1 - h_\theta (x) \)
对上面的表达式合并一下就是:
\( P(y|x;\theta ) = (h_\theta (x))^y(1-h_\theta (x))^{1-y} \)
三、推导过程
梯度上升
得到了逻辑回归的表达式,下一步构建似然函数,然后最大似然估计,最终推导出θ的迭代更新表达式
只不过这里用的不是梯度下降,而是梯度上升,因为这里是最大化似然函数不是最小化似然函数。我们假设训练样本相互独立,那么似然函数表达式为:
同样对似然函数取log,转换为:
转换后的似然函数对θ求偏导,在这里我们以只有一个训练样本的情况为例:
这样我们就得到了梯度上升每次迭代的更新方向,那么\( \theta \)的迭代表达式为:
四、逻辑回归参数
逻辑回归的模型调优一般考虑对其正则惩罚项系数进行调整,sigmoid函数的选择,在实际场景中一般是保证一定精确率(Precision)的情况下尽可能提高召回率(Recall rate)
1)class_weight:类型权重参数,默认None,可以输入"balanced"或者一个字典
该参数用于标示分类模型中各种类型的权重,可以不输入,即不考虑权重,或者说所有类型的权重一样
如果选择输入的话,可以选择balanced让类库自己计算类型权重,或者我们自己输入各个类型的权重,比如对于0,1的二元模型,可以定义class_weight={ 0:0.9, 1:0.1 },这样类型0的权重为90%,而类型1的权重为10%
如果class_weight选择balanced,那么类库会根据训练样本量来计算权重。某种类型样本量越多,则权重越低,样本量越少,则权重越高
sklearn的官方文档中,当class_weight为balanced时,类权重计算方法如下:
n_samples / (n_classes * np.bincount(y)),n_samples为样本数,n_classes为类别数量,np.bincount(y)会输出每个类的样本数,例如y=[1,0,0,1,1],则np.bincount(y)=[2,3]
那么class_weight有什么作用呢?在分类模型中,我们经常会遇到两类问题:
第一种是误分类的代价很高。比如对合法用户和非法用户进行分类,将非法用户分类为合法用户的代价很高,我们宁愿将合法用户分类为非法用户,这时可以人工再甄别,但是却不愿将非法用户分类为合法用户。这时,我们可以适当提高非法用户的权重
第二种是样本是高度失衡的,比如我们有合法用户和非法用户的二元样本数据10000条,里面合法用户有9995条,非法用户只有5条,如果我们不考虑权重,则我们可以将所有的测试集都预测为合法用户,这样预测准确率理论上有99.95%
但是却没有任何意义。这时,我们可以选择balanced,让类库自动提高非法用户样本的权重
提高了某种分类的权重,相比不考虑权重,会有更多的样本分类划分到高权重的类别,从而可以解决上面两类问题
2)sample_weight:样本权重参数
由于样本不平衡导致我们的模型预测能力下降。遇到这种情况,我们可以通过调节样本权重来尝试解决这个问题
调节样本权重的方法有两种,第一种是在class_weight使用balanced。第二种是在调用fit函数时,通过sample_weight来自己调节每个样本权重
在scikit-learn做逻辑回归时,如果上面两种方法都用到了,那么样本的真正权重是class_weight * sample_weight
3)penalty:正则化参数:’l1’,’l2’.默认是’l2’
在调参时如果我们主要的目的只是为了解决过拟合,一般penalty选择L2正则化就够了。但是如果选择L2正则化发现还是过拟合,即预测效果差的时候,就可以考虑L1正则化
另外,如果模型的特征非常多,我们希望一些不重要的特征系数归零,从而让模型系数稀疏化的话,也可以使用L1正则化
penalty参数的选择会影响我们损失函数优化算法的选择。即参数solver的选择
4)C:smaller values specify stronger regularization