滤波操作(均值、高斯、中值、双边)

各种滤波操作(均值、高斯、中值、双边)

如何判断边缘

1：在图像的边缘部分，像素值的变化较为剧烈。
2：在图像的非边缘区域，像素值的变换较为平坦。

想要保留图像边缘，必须引入一个能够衡量图像像素变换剧烈程度的变量。

线性滤波

滤波分为高通滤波、低通滤波、带通滤波、带阻滤波。

滤波是对输入信号进行卷积处理的一个过程，写成一个表达式的形式是这样的：
滤波 = 卷积（ 输入信号 ，卷积模板 ）， 卷积模板/掩膜 的不同决定了不同的滤波方式，也因此产生了高通、低通、带通、带阻等基本的滤波方式。

针对低通滤波，就是保留将信号中的低频部分，抑制高频部分。要达到这个目的，可以利用均值掩膜、高斯掩膜等对输入信号进行处理。
采用均值掩膜对输入信号进行卷积的滤波方式叫均值滤波；
采用高斯掩膜对输入信号进行卷积的滤波方式叫高斯滤波；

高通滤波常见的有理想高通滤波和巴特沃斯高通滤波，在opencv领域并不常用。本文主要讲解低通滤波。

滤波原理

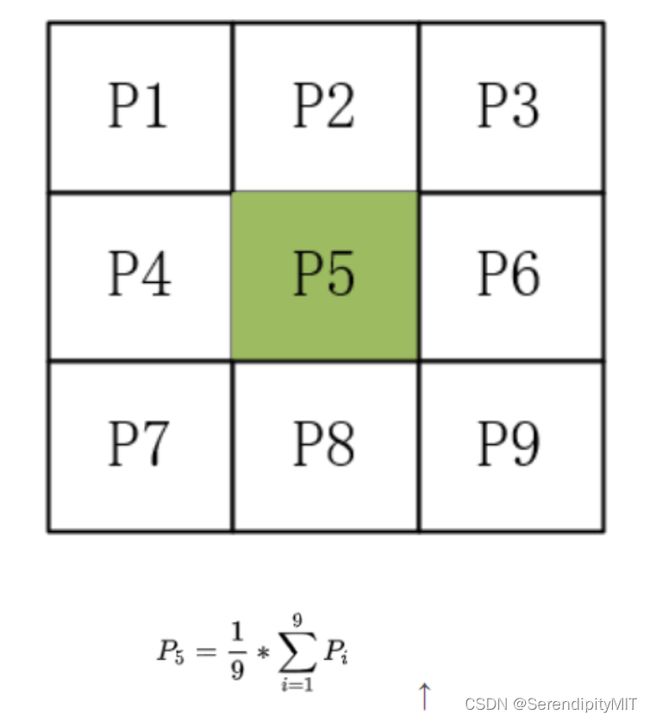
滤波就是对整幅图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到。

以3 *3 大小的卷积核为例进行滤波，原理如下：

均值滤波

函数API如下：

void blur(
    InputArray src, 
    OutputArray dst, 
    Size ksize, 
    Point anchor=Point(-1,-1), 
    int borderType=BORDER_DEFAULT 
		)
    src:输入图像
	dst:输出图像
	ksize:卷积核大小
	anchor:锚点位置
	borderType:当要扩充输入图像矩阵边界时的像素取值方法，当核矩阵锚点与像素重合但核矩阵覆盖范围超出到图像外时，函数可以根据指定的边界模式进行插值运算。（可以忽略，让API默认使用）

常用的borderType类型：

理想的均值滤波是用每个像素和它周围像素计算出来的平均值替换图像中每个像素，均值滤波特点就是卷积核的内容都是1这个数字。上图p1 - p9 都是1。

均值滤波运行结果如下：

高斯滤波

高斯滤波和均值滤波唯一不同的是高斯滤波的卷积元素的数值是中间的最大，距离中间点越远值越小。符合二维正态分布。API如下：

void GaussianBlur(
	InputArray src, 
	OutputArray dst, 
	Size ksize, 
    double sigmaX, 
    double sigmaY=0,
    int borderType=BORDER_DEFAULT 
    )
    src:输入图像
    dst:输出图像
    ksize:卷积核大小
    sigmaX:卷积核在水平方向上（X 轴方向）的标准差，其控制的是权重比例
    sigmaY:卷积核在垂直方向上（Y 轴方向）的标准差，其控制的是权重比例（可以不设定）
    borderType:与API blur()一样

注意：sigmaX是必选参数。sigmaY是可选参数，选择0的话就跟随sigmaX。如果sigmaX设为0，那么sigmaX和sigmaY都由编译器自动去计算。如果两者都是0，那么分别由ksize.width和ksize.height计算得到：

sigmaX = 0.3×[(ksize.width-1)×0.5-1] + 0.8
sigmaY = 0.3×[(ksize.height-1)×0.5-1] + 0.8

高斯滤波的应用结果：

非线性滤波

中值滤波

如果一个信号是平缓变化的，那么某一点的输出值可以用这点的某个大小的邻域内的所有值的统计中值来代替。这个邻域在信号处理领域称之为窗0（window）或者模板（Mask）。模板开的越大，输出的结果就越平滑，但也可能会把我们有用的信号特征给抹掉。所以窗的大小要根据实际的信号和噪声特性来确定。通常我们会选择窗的大小使得窗内的数据个数为奇数个，之所以这么选是因为奇数个数据才有唯一的中间值。

中间值用这九个数字的中值来代替。缺点是处理前要排序，耗费时间长，是均值滤波的五倍左右。

API如下：

void medianBlur( 
	InputArray src, 
	OutputArray dst, 
	int ksize 
);
src:输入图像
dst:输出图像
ksize:卷积核大小，必须是奇数

双边滤波

双边滤波(Bilateral Filters)是非常常用的一种滤波，它可以达到保持边缘、降噪平滑的效果。和其他滤波原理一样，双边滤波也是采用加权平均的方法，用周边像素亮度值的加权平均代表某个像素的强度，所用的加权平均基于高斯分布。最重要的是，双边滤波的权重不仅考虑了像素的欧氏距离（如普通的高斯低通滤波，只考虑了位置对中心像素的影响），还考虑了像素范围域中的辐射差异（例如卷积核中像素与中心像素之间相似程度、颜色强度，深度距离等）。

双边滤波原理

双边滤波原理公式：

其中：

这个公式没必要懂，请看解析：

假设我们要对这样一个10 *10 的图像进行双边滤波操作，选取一个5 * 5的卷积核，如图所示：（图片截取自他人）

计算机图形中的原点都是从左上角开始，向右为X的正向轴，向下为Y的正向轴，坐标都从0开始。

那么146就是卷积核的中心像素点，坐标为（2,2），165像素点坐标为（0,0）。

参数解析：q就是选取/输入的像素点，先不考虑求和公式∑ 与 q∈S。Gσs是空间域核，Gσr是图像像素域核。（这里两个专业名词不用懂，继续往下看）。这是两个二维高斯函数，二维高斯函数的公式为：

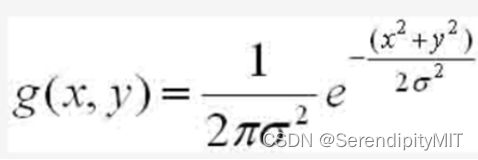
他们两者的本质是这样的，但实际表现内容是这样子：

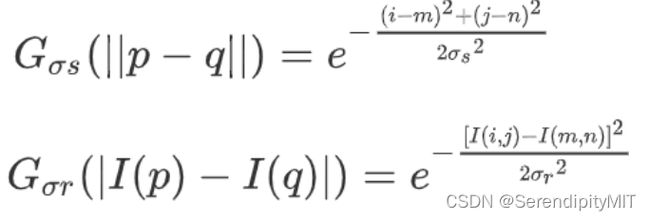
q代表输入像素点，m与n是输入像素的横坐标与纵坐标，p是方框中心像素点，i与j是方框中心像素的坐标，I(m,n)代表输入像素的值，I(i,j)代表方框中心像素的值。σs与σr是我们设定的值。比如：165这个像素点，坐标为（0，0），那么m = n = 0、I(m,n) = I(0,0) = 165、方框中心点的坐标为（2，2），i = 2，j = 2，I（2，2） = 146.

那么实际操作是这样的：

①首先遍历整个5×5的小框，第一个遍历到的点是165，它的坐标是(0,0),像素值是165，
那么中心点与该点的空间域计算结果为：

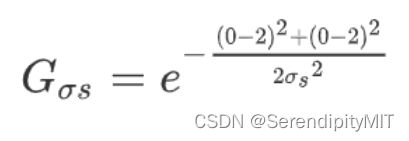
②再计算中心点与该点的像素域结果：

当 σs = 5 σs = 20 时Gσs = 0.8521，Gσr = 0.6368。如此循环遍历整个图像，得到检测到的每一个像素点的空间域与像素域的值，将Gs * Gr 的结果记为 Wp。求将检测到的每一个像素点的Wp相加就是公式的分母，这也就是求和公式的作用。分子是所有像素Wp * I(m,n)的和（I(m,n)是像素点的值）。等式左边就是输出的像素点的值，们将小框从左往右，从上往下不断移动，按照我们的算法不断更新方框中心的像素值，就得到了双边算法的输出。

SERENDIPITY