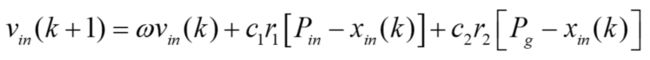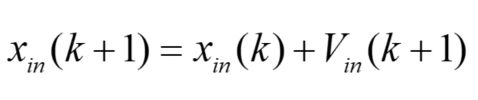图说粒子群优化算法(PSO)附源码

前面说了ACO，这次就来说下PSO吧。

目录

一、初识PSO：这是个啥玩意？

二、PSO的数学原理

三、MATLAB代码

---

一、初识PSO：这是个啥玩意？

粒子群优化算法是模拟鸟群觅食行为的一种优化算法，它通过自身及群体搜索的经验来寻找全局最优解。没错，ACO模拟的蚁群觅食，PSO模拟的是鸟群觅食！但是作用却不一样，一个是寻找最优路径的，一个是用来做优化的。

粒子群算法被广泛用于求极值的问题。在鸟群觅食过程中，个体鸟与群体之存在一种信息共享机制，鸟儿会根据自身搜索经验和群体搜索经验来时时调整自己的飞行状态，以期找到实物最多的地方。该算法适用于求极值的问题。关于鸟群觅食的过程，还是上图解释吧：

图1 鸟群觅食图解

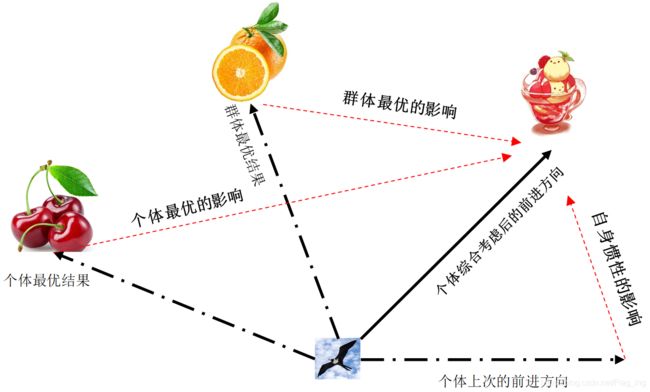
如图1所示，假设鸟群在随机搜索食物，如果已知在某块区域里有一块食物，但所有的鸟都不知道这块食物具体位置，不过它们能通过自身的经验(个体最优)和群体经验(群体最优)来预判得到当前的位置离食物还有多远，从而很快找到食物的位置。PSO正是从这种机制中得到了启发，PSO的基础是信息的群体共享。

基于以上鸟对群觅食原理的解析，PSO算法可以描述为：将要求解的模型函数的变量当作“鸟群”即粒子，粒子的维度对应自变量的数量。刚开始，每个粒子有一个初始化的位置(对应该变量取一定值时的函数值)和加速度(对应变量取值的变化量)，每次粒子的位置更新后都会进行粒子个体与群体最优位置的更新，然后根据最新的最优位置对粒子个体的速度进行更新，并进行下一轮飞行测试，直到所有粒子找到最优位置即最优解。

粒子群算法流程可描述如下：

1. 对粒子的加速度(自变量速度变化量)进行初始化，并随机初始化粒子群的初速度(自变量数值初始变化量)与位置(自变量取值的)；
2. 计算所有粒子当前所在位置对应的模型函数(或者说目标函数、适应度函数)的值；
3. 更新本次迭代中粒子个体与群体的历史最优位置；
4. 根据以上更新的历史最优位置更新粒子的下一步飞行的速度及位置；
5. 重复第2~5步，直到个体最优值不在发生变化或达到指定迭代次数。

二、PSO的数学原理

在一中，我们了解了自然界鸟群的觅食过程，而将这一过程进行数学化描述就是PSO算法了。在上面对鸟群觅食的描述中我们可以发现几个关键词：鸟群(N)，速度更新(v)，位置更新(x)。如何对这些关键词数学化呐？且听我慢慢道来。

举一个简单的一维函数的栗子，假设我们要优化的函数为：

                                                                     
我们的目的是：在x取值范围一定时，找到一个x的值，使得目标函数(也叫适应度函数)f(x)的取值最大。

1、首先我们要初始化粒子(对应自变量x)个数N，迭代次数K并随即初始化他们的位置(对应自变量x的取值)

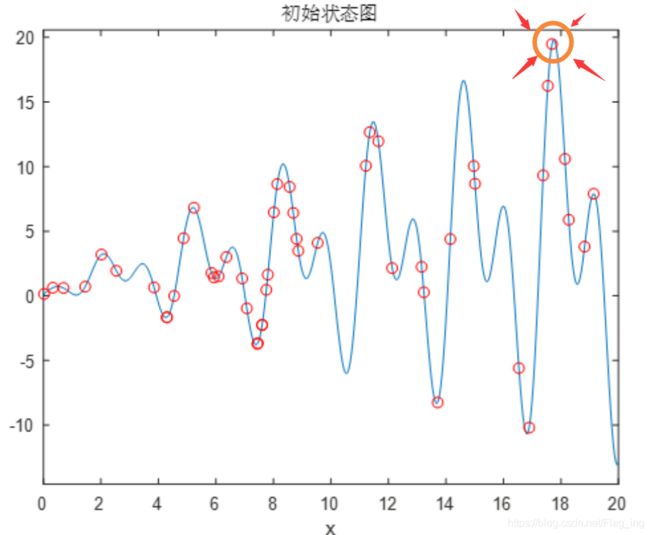
N和K的值都不要太小，N、K怎么也得有个二三十往上吧，但也别太大，太大的话就太为难这小笔记本电脑咯。我们看一下粒子初始化位置后的效果吧，红色的全就是粒子所在的位置。

图2 粒子的初始化位置

看着这个初始化的图，我们可以想象这么一个过程： 在某一轮迭代中，这一群粒各自瞅了下自己的位置，再跟自己原来呆过的位置比了下，诶找出了自己历史上的一个最好的位置，然后总结下自身地经验，并记下这个位置的方向和距离。然后再瞄几眼别人的位置，诶又找到了整体的历史最优位置(因为这个图是初始化位置，所以此时整体历史最优解就是图中橙色圈标出的哪个红色圈)，然后又记下了这个最好粒子的位置方向和距离，心里想着：得向这个大佬看齐。在下次迭代中，每颗粒子当然都想让自己站的更高(函数值最大)，怎么办那？那就总结自己的经验+参考别人的经验继续“前进”呗，就这么一想，就朝着自己综合判断的方向走去了，但是一步不能走太多，容易走过头，所以每走一步得给自己限制下步距。。。。。。就这样周而复始地迭代，最终所有有点脑子的粒子都能站上粒生的巅峰！对于没脑子的粒子没走上人生巅峰咋办呐？那就不管了呗，因为我们最终只看最优秀的粒子所处的位置，hhh世界这就是这么残酷。。。

2、更新粒子的速度(对应自变量x的变化量)

粒子的速度更新公式如下式所示：

式中，表示第k+1次迭代粒子i飞行速度的第n维(多少维就是多少个自变量的意思)分量，这里我们只有1维分量，所以n就是1了。表示第k次迭代粒子i位置的第n维分量，为一个非负的惯性权重，调节对解空间的搜索范围，、为加速度常数，调节速度变化的最大步长，可以理解为学习率，、为两个随机数函数，用以增加搜索的随机性，取值范围为[0,1]，与分别表示个体和群体经过的最好位置。分析该公式中的三个部分可知，其分别对应图1的个体上次前进方向，个体最优结果以及群体最优结果这三种影响。

3、更新粒子的位置(对应自变量x的值)

位置更新公式如下：

式中代表粒子上次的位置，表示更新之后的位置。

4、整个PSO算法主要就靠2、3两个公式sao下去，通过不断迭代，得到当前最优解的结果。

最后总结一下：粒子群算法是一种随机搜索算法，粒子选择下一步飞行的方向和速度是自身历史最优位置以及群体历史最优位置综合影响的结果，并总是趋向于向最优解方向飞行，在飞行过程中直要个体或群体最优位置发生变化，个体都会立即调整当前飞行状态，向认为的最优解方向飞行，这样大大提高了粒子寻找最优解的效率，同时使得这个更新过程具有了潜在的指导，而并非盲目的随机。

三、MATLAB代码

% 初始化种群
f= @(x)x .* sin(x) .* cos(3 * x)+x.^0.5; % 函数表达式
figure(1);ezplot(f,[0,0.01,20]);
N = 50;                         % 初始种群个数
d = 1;                          % 空间维数
K = 50;                      % 最大迭代次数
limit = [0, 20];                % 设置位置参数限制
vlimit = [-1, 1];               % 设置速度限制
w = 0.8;                        % 惯性权重
c1 = 0.5;                       % 自我学习因子
c2 = 0.5;                       % 群体学习因子 
for i = 1:d
    x = limit(i, 1) + (limit(i, 2) - limit(i, 1)) * rand(N, d);%初始种群的位置
end
v = rand(N, d);                  % 初始种群的速度
xm = x;                          % 每个个体的历史最佳位置
ym = zeros(1, d);                % 种群的历史最佳位置
fxm = zeros(N, 1);               % 每个个体的历史最佳适应度
fym = -inf;                      % 种群历史最佳适应度
hold on
plot(xm, f(xm), 'ro');title('初始状态图');
figure(2)
% 群体更新
iter = 1;
record = zeros(K, 1);          % 记录器
while iter <= K
     fx = f(x) ; % 个体当前适应度   
     for i = 1:N      
        if fxm(i) < fx(i)
            fxm(i) = fx(i);     % 更新个体历史最佳适应度
            xm(i,:) = x(i,:);   % 更新个体历史最佳位置
        end 
     end
if fym < max(fxm)
        [fym, nmax] = max(fxm);   % 更新群体历史最佳适应度
        ym = xm(nmax, :);      % 更新群体历史最佳位置
 end
    v = v * w + c1 * rand * (xm - x) + c2 * rand * (repmat(ym, N, 1) - x);% 速度更新
    % 边界速度处理
    v(v > vlimit(2)) = vlimit(2);
    v(v < vlimit(1)) = vlimit(1);
    x = x + v;% 位置更新
    % 边界位置处理
    x(x > limit(2)) = limit(2);
    x(x < limit(1)) = limit(1);
    record(iter) = fym;%最大值记录
    % 绘制中间状态图
    x0 = 0 : 0.01 : 20;
    plot(x0, f(x0), 'b-', x, f(x), 'ro');title('状态位置变化')
    pause(0.1)  % 暂停0.1s后继续执行

    iter = iter+1;
end
figure(3);plot(record);title('收敛过程')
x0 = 0 : 0.01 : 20;
figure(4);plot(x0, f(x0), 'b-', x, f(x), 'ro');title('最终状态位置')
disp(['最大值：',num2str(fym)]);
disp(['变量取值：',num2str(ym)]);

四、结果：要不自己运行下试试？？我觉得可以hhhh——此处省略咯