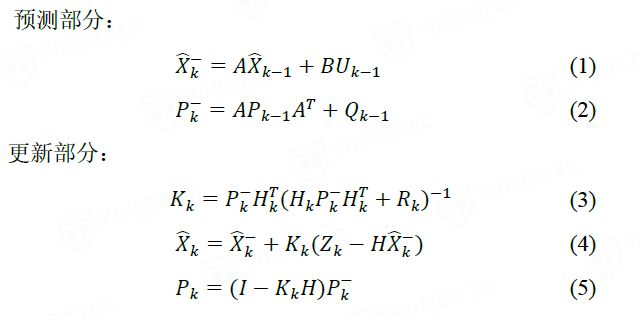六轴传感器+卡尔曼滤波+一阶低通滤波
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 角度与角速度测量
-
-
- 1.角度与角速度获取
- 2 互补滤波
- 3卡尔曼滤波
- 4 实现卡尔一阶低通滤波
- 5 实现卡尔曼滤波算法
-
角度与角速度测量
1.角度与角速度获取
直立控制是通过角度与角速度反馈来进行的,所以角度与角速度的测量至关重要。本系统使用 MPU6050 作为姿态传感器,集成一个加速度传感器和一个陀螺仪,可以输出三轴的加速度与角速度。角速度的获取可以通过陀螺仪来直接读取,角度的获取可以有两种方法来测量:一是通过加速度计的加速度分量来计算,二是通过陀螺仪输出的角速度进行积分获得。
MPU6050 的坐标系定义如图1-1 。

当传感器的正方向Z 轴垂直指向天空时,由于此时受到地球重力的作用,此时加速度计Z 轴的读数应为正,而且理想情况下应为g。注意此时读取加速度计并不是重力加速度,而是物体自身的运动加速度,正因为自身的运动加速度与重力加速度大小相等方向相反,芯片才能保持静止。
当传感器静止不动时,我们仅绕X 轴旋转一定的角度θ,此时加速度方向一直与X 轴垂直,X 轴并无加速度分量,忽略X 轴,把加速度分解,如图2-2 所示,可以很容易就算出传感器绕X 轴的角度。


当仅绕Y 轴旋转时也是同样的原理。当绕Z 轴旋转时,因为重力加速度固定为Z 轴方向,故在X 与Y 轴无加速度分量,仅仅通过加速度计无法得出绕Z轴角度,若想得到绕Z 轴角度,只能通过角速度积分获得,但因为有偏差,一段时间后将不再具有参考意义。
物体的旋转运动就是绕三轴旋转角度的叠加,我们读取加速度计的数据,根据公式进行处理就可以获取相应的姿态角。故小车绕X 轴与Y 轴的角度可用以下公式算出:

在完全静止的情况下确实通过加速度计就可以获取到所需的角度,但是在实际应用中,小车因为车身摆动等情况会产生加速度,它叠加在测量信号上会无法准确地反映出车模的倾角,图1-3 所示。

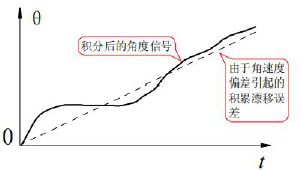
那么通过陀螺仪的角速度进行积分得到角度呢?如果测量的角速度存在微小的误差或漂移,经过积分运算之后,形成积累误差,随着时间增加,角度信息将不再准确,这一个方法也是不太可行的。
我们可以综合加速度计和陀螺仪的角度,进行滤波和平滑处理得到准确的角度。程序提供了三种得到准确的角度的算法:1.DMP 算法2.互补滤波算法3.卡尔曼滤波算法。
DMP 算法是MPU6050 自带的一种滤波方法,只要进行一些初始化,使用官方的库函数就可以读取出四元数,根据公式就可以计算出姿态角。
2 互补滤波
通过加速度计和陀螺仪获取的角度都有一定的缺点,加速度计获取的角度长期来看比较准确,但是波动大,可以认为其掺杂了高频噪声;陀螺仪获取的角度短时间比较准确,但有积分误差,可以认为其掺杂了低频噪声。我们可以分别让他们通过一个低通滤波器和一个高通滤波器然后叠加在一起,这就是互补滤波算法。


对应我们的代码为:
angle = K1 * angle_m+ (1-K1) * (angle + gyro_m * dt);
可以看出,互补滤波就是通过加速度计获取的角度对陀螺仪积分的角度进行校准,从而积分的角度逐步跟踪到加速度传感器所得到的角度。K1 与1-K1 是对这两个角度取不同的权重,可以表示我们对不同数据的信任程度。
3卡尔曼滤波
传感器测量的数据总是有很多的不确定性,比如有很多的噪声,而这些噪声大部分都符合高斯分布。对于我们的小车,输入是角速度,输出是角度,这是一个线性的系统。如果一个系统是线性的系统,而且这些不确定性是符合高斯分布的,那么我们就可以使用卡尔曼滤波算法进行最优估计。卡尔曼滤波的思想就是使用系统的状态方程预测当前的值,使用传感器测出来的观测值来修正这个预测值。与互补滤波一样,可以选择不同的权重来实现,但是这个权重是动态变化的。我们知道一个系统的状态方程和传感器的测量方程如下:
4 实现卡尔一阶低通滤波
/****************************** BEFIN ********************************
**
**@Name : Complementary_Filter_x
**@Brief : 一阶互补滤波
**@Param angle_m: 加速度算出的角度
** gyro_m: 陀螺仪的角速度
**@Return : None
**@Author : @mayuxin
**@Data : 2022-06-04
******************************** END *********************************/
float Complementary_Filter_x(float angle_m, float gyro_m)
{
static float angle;
float K1 =0.02;
angle = K1 * angle_m+ (1-K1) * (angle + gyro_m * dt);
return angle;
}
5 实现卡尔曼滤波算法
/****************************** BEFIN ********************************
**
**@Name : Kalman_Filter_x
**@Brief : 获取x轴角度简易卡尔曼滤波
**@Param Accel: 加速度算出的角度
** Gyro: 陀螺仪的角速度
**@Return : None
**@Author : @mayuxin
**@Data : 2022-06-04
******************************** END *********************************/
float dt=0.005; //每5ms进行一次滤波
float Kalman_Filter_x(float Accel,float Gyro)
{
static float angle_dot;
static float angle;
float Q_angle=0.001; // 过程噪声的协方差
float Q_gyro=0.003; //0.003 过程噪声的协方差 过程噪声的协方差为一个一行两列矩阵
float R_angle=0.5; // 测量噪声的协方差 既测量偏差
char C_0 = 1;
static float Q_bias, Angle_err;
static float PCt_0, PCt_1, E;
static float K_0, K_1, t_0, t_1;
static float Pdot[4] ={0,0,0,0};
static float PP[2][2] = { { 1, 0 },{ 0, 1 } };
angle+=(Gyro - Q_bias) * dt; //先验估计
Pdot[0]=Q_angle - PP[0][1] - PP[1][0]; // Pk-先验估计误差协方差的微分
Pdot[1]=-PP[1][1];
Pdot[2]=-PP[1][1];
Pdot[3]=Q_gyro;
PP[0][0] += Pdot[0] * dt; // Pk-先验估计误差协方差微分的积分
PP[0][1] += Pdot[1] * dt; // =先验估计误差协方差
PP[1][0] += Pdot[2] * dt;
PP[1][1] += Pdot[3] * dt;
Angle_err = Accel - angle; //zk-先验估计
PCt_0 = C_0 * PP[0][0];
PCt_1 = C_0 * PP[1][0];
E = R_angle + C_0 * PCt_0;
K_0 = PCt_0 / E;
K_1 = PCt_1 / E;
t_0 = PCt_0;
t_1 = C_0 * PP[0][1];
PP[0][0] -= K_0 * t_0; //后验估计误差协方差
PP[0][1] -= K_0 * t_1;
PP[1][0] -= K_1 * t_0;
PP[1][1] -= K_1 * t_1;
angle += K_0 * Angle_err; //后验估计
Q_bias += K_1 * Angle_err; //后验估计
angle_dot = Gyro - Q_bias; //输出值(后验估计)的微分=角速度
return angle;
}