经典智能算法之粒子群算法详解
经典智能算法之粒子群算法
要理解粒子群算法怎么可能没有算法背景,请看
算法历史
粒子群优化(Particle Swarm Optimization, PSO)算法是Kennedy和Eberhart受人工生命研究结果的启发、通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的全局随机搜索算法。
自然界中各种生物体均具有一定的群体行为,而人工生命的主要研究领域之一是探索自然界生物的群体行为,从而在计算机上构建其群体模型。生物学家Craig Reynolds在1987年提出了一个非常有影响的鸟群聚集模型,对其进行仿真,结果非常接近的模拟出鸟群飞行的现象。1995年,美国社会心理学家James Kennedy和电气工程师Russell Eberhart共同提出了粒子群算法,其基本思想是受对鸟类群体行为进行建模与仿真的研究结果的启发。他们的模型和仿真算法主要对Frank Heppner的模型进行了修正,以使粒子飞向解空间并在最好解处降落。
基本思想
POS 初始化为一群随机粒子(随机解)。然后通过迭代找到最优解在每一次迭代中,粒子通过跟踪两个"极值"来更新自己。第一个就是粒子本身所找到的最优解,这个解叫做个体极值。另一个极值是整个种群目前找到的最优解,这个极值是全局极值。另外也可以不用整个种群而只是用其中一部分作为粒子的邻居,那么在所有邻居中的极值就是局部极值。
来吧,各位我们直奔核心
迭代公式
v i d = w ∗ v i d + c 1 r 1 ( p i d − x i d ) + c 2 r 2 ( p g d − x i d ) v_{id} = w*v_{id} + c_1r_1(p_{id}-x_{id})+c_2r_2(p_{gd}-x_{id}) vid=w∗vid+c1r1(pid−xid)+c2r2(pgd−xid)
x i d = x i d + v i d x_{id} = x_{id} + v_{id} xid=xid+vid
(1)大体了解一下
式子1中右边由三部分组成
-
第一部分代表了粒子保持先前速度的趋势,相当于物理学的惯性或者动量
-
第二部分代表了粒子对自身经验的记忆,相当于生物学意义上的认知
-
第三部分代表了粒子之间协同的社会影响,相当于群体学上的社会
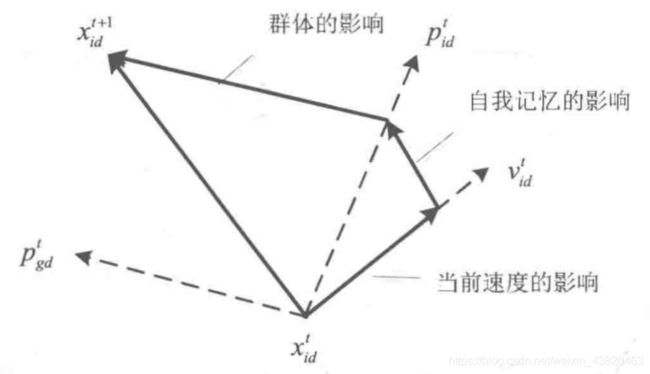
剩下的部分应该很好理解,你是不是感觉上面迭代式写的有点像程序中的赋值语句(哈哈,不错就是赋值),如果感觉不好理解的话,我们可以把上式左边的下边换为t+1,右边换为t,(表示随着时间更新)就好理解了,这里仅示范下面那个迭代式,即:
x t + 1 = x t + v t x_{t+1}=x_t+v_t xt+1=xt+vt
(2)认识各个参数
——w惯性权重
——c1,c2学习因子
——r2,r2 [0,1]的随机数
(上述参数是怎么设置,又该怎么算,我一窍不通哈,可以忽略不看)
——Pid,Pgd 两极值就是前面说的两个极值,千万别弄错了
这里需要解释一下下
1. 这两个极值是什么
一个称为个体极值,是单个粒子截止现在时刻搜索到的最优位置
一个称为全局极值,是整个粒子群截止现在时刻搜索到的最优位置
这么看来,这两个值不一定相同呀!
2. 这个极值怎么表示
如果位置只是轴线上的一个点,即一维的。哈哈,很简单用一个数就可以了
如果位置是平面上的一个点,即二维的。这个也很简单用有序数对(x,y)表示
如果位置是空间上的一个点,即三维的。这个我也知道是用(x, y, z)表示
……
这样好麻烦,我们想到了用D维向量表示即
其中i代表第i个粒子。
X i = ( x i 1 , x i 2 , . . . , x i D ) X_i=(x_{i1},x_{i2},...,x_{iD}) Xi=(xi1,xi2,...,xiD)
很好,这样我们也会表示极值了
3. 这个极值怎么求的
求这个极值可是极其关键的部分,也正是它起推动作用的。既然是极值,我们肯定要用一个参数或标准来衡量谁优,不同的领域衡量的方式不同,但最后都要归到数学模型,具体来说就是一个函数表达式。(吹了这么多牛逼就是一个函数呀)对,在程序里就是个函数。不过,它在这里有一个高大上的专业名称叫适应度。
就是因为数学模型,这个算法就可以应用到许多领域,各位老铁应该在检索论文的时候看到很多应用了吧。嗯嗯,只要你会点数学建模,来个实际应用,你就可以发表论文了,哈哈,就这么简单。但是本人觉得各行各业的应用固然重要,但是更重要的是基础科学的研究,这才是核心呀!(题外话)
(3)通俗理解算法
哈哈先看图,这图有点太花哨(不是原创,个人编辑图片能力不是很强)
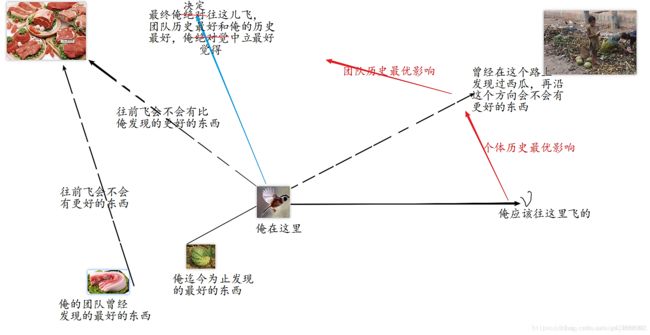
粒子群算法就是根据鸟群来的,那我们就谈谈鸟群吧。正如上图所示:
鸟儿变化后的速度跟三个方面有关,首先就是与前一刻的速度有关,变化需要基准和代价的,不能随意变向和变大小(鸟儿不可能把自己速度一下提升为无穷大吧)肯定要考虑之前速度。当然,鸟儿肯定很想吃东西,它的印象中好像上次在某个方向上发现很好吃的虫子,这次那个方向会不会也有好吃的,哈哈,是要考虑一下。最后,它的队友们曾经在另一个方向上找到最好吃的东西,还很多,这次会不会还向上次一样运气那么好。当然它一部分队友说的也可以(局部最优)。它考虑一番后,作出了如图决定。
所以这是粒子群算法的原理,哈哈,应该理解了吧!
程序设计
讲了那么多原理,该怎么写程序呢,接下来我们就来考虑一下细节。
初始化
首先我们要有一个随机粒子群,每个粒子群应该具有位置和速度两个属性,在MATLAB里实现就是想下面这样:
for i=1:N
for j=1:D
x(i,j) = randn; %随机初始化位置
v(i,j) = randn; %随机初始化速度
end
end
接下来就是寻找两极值了。
找极值
找极值之前应该先有一个衡量,对,就是上面说的适应度,现在我们抽象一下,称它为fitness吧,它的具体的实现交给具体的任务吧。
全局极值
全局最优此刻通过适应度函数就可以找到了,MATLAB代码即:
for i=1:N
p(i) = fitness(x(i,:)); %x(i,:)即代表单个的粒子哦
y(i,:) = x(i,:);
end
pg=x(N,:); %全局最优
for i = i:(N-1)
if fitness(x(i,:)) < fitness(pg)
pg = x(i,:);
end
end
个体极值
个体更新后可以通过之前做比较来寻找,前提必须是有更新,所以比全局极值少一次哦(少第一次,第一次就是最有不用比较哦),只需要把上一刻极值和更新后的适应度比较就可以喽,哈哈,简单的一个判断就行了。不要忘了全局极值也要更新哦,所有个体极值的极值就是全局极值,哈哈哈,一样一个if就可以实现(产生的每个个体极值跟全局极值比较就好了)。所以MATLAB程序就是:
for t = 1:M
for i = 1:N
v(i,:) = w*v(i,:) + c1*rand*(y(i,:)-x(i,:)) + c2*rand*(pg - x(i,:));
x(i,:) = x(i,:) + v(i,:);
if fitness(x(i,:)) < p(i)
pi = fitness(x(i,:));
y(i,:) = x(i,:);
end
if p(i) < fitness(pg)
pg = y(i,:);
end
end
Pbest(t) = fitness(pg);
end
哈哈哈,大功告成,不不不,还要把结果输出。
最后,把代码整理一下,确定参数,还有一些细节,如最大迭代次数,搜索范围,种群粒子个数,解空间维数等等,大家估计发现就是书上的代码,哈哈这就被你们发现。赶快,在理一下思路,看下面流程图:

哈哈,小编不才,亲自敲了一遍,大家如果有需要可以自行下载。不过,我还是希望大家亲自敲一遍。
不过小编在这里想推荐一个大佬写的博客代码历程,看了你们会理解更深刻哦!
CSDN博客
如果文章有用,欢迎点赞、打赏、转发。最重要的还是要谢谢大家的支持,我会一如既往地推送深度好文…
 |
 |