《人工智能-机器学习》数据预处理和机器学习算法(以企鹅penguins数据集为例)
文章目录
- 一、数据预处理
-
- 1 内容和目标:
- 2 加载和分析数据
-
- 2.1 导入基本库和加载数据
- 2.2 分析数据
- 3 数据清洗
-
- 3.1 重复值处理
- 3.2 数据脱敏—提取重要特征
- 3.3 缺失值处理
- 3.4 异常值处理
- 3.5 标签编码或独热编码
- 4 其他处理
-
- 4.1 利用value_counts函数查看每个类别数量
- 4.2 特征与标签组合的散点可视化
- 二、机器学习算法
-
- 1 数据归一化和划分
-
- 1.1 数据归一化处理
- 1.2 数据集划分
- 2 算法应用
-
- 2.1 算法实现
- 2.2 算法评估与分析
-
- 2.2.1 模型特征重要性andPermutation Importance
- 2.2.2 提取特征可视化
- 3 其他常用机器学习算法的封装(分类)
本项目使用到的数据集链接:
https://tianchi-media.oss-cn-beijing.aliyuncs.com/DSW/6tree/penguins_raw.csv
一、数据预处理
1 内容和目标:
加载给定或者自行选定的数据集,对数据进行查看和理解,例如样本数量,各特征数据类型、分布、特征和标签所表达的含义等,然后对其进行数据预处理工作,包括但不限于对敏感数据、缺失值、重复值、异常值等进行统计和处理,对标签数据进行编码,对特征进行标准化或归一化等,最终获得干净整洁的数据集以便于后续的算法模型进行处理。
2 加载和分析数据
2.1 导入基本库和加载数据
# 基础函数库
import numpy as np
import pandas as pd
# 绘图函数库
import matplotlib.pyplot as plt
import seaborn as sns
我们利用pandas自带的read_csv函数读取并转化为DataFrame格式
data = pd.read_csv('./penguins_raw.csv')
2.2 分析数据
①查看数据集大小
data.shape
## output: (344, 17) 该原始数据集包含344行(个),17列(特征)的数据。
②利用.info()查看数据的整体信息
data.info()
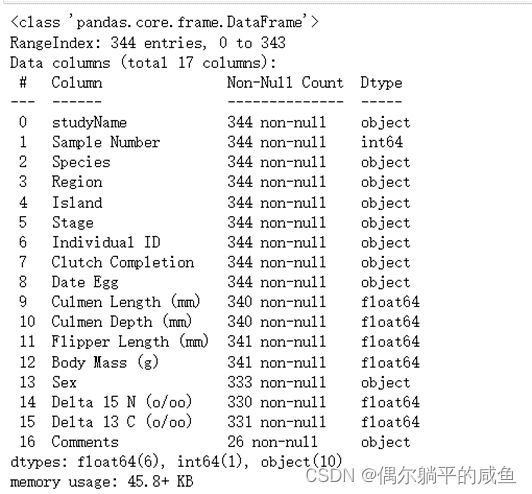
可以看出一共有17列,每一列的非空值个数以及值的类型。其中studyName、Species、Region、Island、Stage、Individual ID、Clutch Completion、Date Egg、Sex、Comments是分类指标、Sampe Number为整数、其他为float64类型组成,数据集样本数量为 340,数据不完整、包含缺失值。
③describe() 函数可以查看数值数据的基本情况
包括count 非空值数、mean 平均值、std 标准差、max 最大值、min 最小值、(25%、50%、75%)分位数
data.describe()

④查看前5行数据 [.head() 头部、 .tail()尾部]
data.head(5) # data.tail(5)
3 数据清洗
3.1 重复值处理
分析数据可知,’studyName’,‘Sample Number’,'Individual ID’三个属性唯一确定一条数据。
data[data.duplicated(['studyName','Sample Number','Individual ID'])]
# data[data.duplicated()] 以全部属性为标准的缺失值
# data.drop([339]) #若存在缺失值,根据所提示出的行索引删除即可
3.2 数据脱敏—提取重要特征
为了方便我们仅选与企鹅本身关联较大的特征,经过查阅资料,我们将定量(喙长Culmen Length (mm)、喙深Culmen Depth (mm)、鳍长Flipper Length (mm)和身体质量Body Mass (g))和定性(性别Sex)特征作为输入,这些特征唯一地描述一个企鹅,输出特征为Species,将企鹅进行分类任务。
data = data[['Species', 'Culmen Length (mm)','Culmen Depth (mm)', 'Flipper Length (mm)','Body Mass (g)','Sex']]
3.3 缺失值处理
①查看数据缺失情况
data.isnull().sum()
②分析数据间的相关性
# 使用皮尔森计算特征相关矩阵
corr = data.corr(method='pearson')
# 热力图绘制相关性矩阵
sns.heatmap(data=corr, annot=True, cmap='coolwarm')
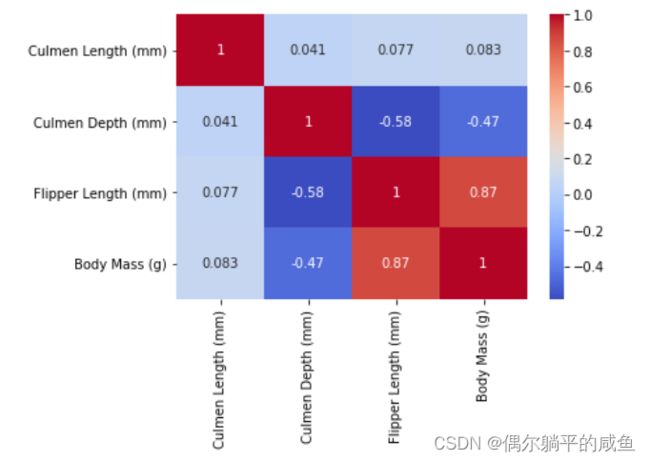
根据图中数据,可以看到缺失值特征与其它特性相关性均不大,因而通过其它特征进行填充的方案不可行,结合数据理解部分的统计结果,故直接才用均值进行填充可能更为简单直接一些。
③处理缺失值
这里我们发现数据中存在缺失值,考虑到企鹅数据的实际意义,我们不能将缺失的数据删除,故采用均值插补对连续的缺失值进行处理,对于离散的分类数据值,我们采用MALE进行填补。
data['Culmen Length (mm)']=data['Culmen Length (mm)'].fillna(data['Culmen Length (mm)'].mean())
data['Culmen Depth (mm)']=data['Culmen Depth (mm)'].fillna(data['Culmen Depth (mm)'].mean())
data['Flipper Length (mm)']=data['Flipper Length (mm)'].fillna(data['Flipper Length (mm)'].mean())
data['Body Mass (g)']=data['Body Mass (g)'].fillna(data['Body Mass (g)'].mean())
data['Sex']=data['Sex'].fillna(‘MALE’)
3.4 异常值处理
使用 3σ 法则识别异常值,并使用均值对其进行填充处理。
list = ['Culmen Length (mm)','Culmen Depth (mm)','Flipper Length (mm)','Body Mass (g)']
for i in range(len(list)):
# 使用 3σ 法则识别异常值
col = data[list[i]]
condition = (col - col.mean()).abs() > 3 * col.std()
# 显示找到的异常值
indices = np.arange(col.shape[0])[condition]
print(list[i])
print(col.loc[indices])
根据得出的行索引修改异常值
data.loc[[35,50],['Culmen Length (mm)']]=data['Culmen Length (mm)'].mean()
3.5 标签编码或独热编码
# 对目标值进行标签编码
target = data[‘Species']
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
data[‘Species'] = encoder.fit_transform(target) data[‘Species'].unique()
# 对Sex进行标签编码
target = data[‘Sex']
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
data[‘Sex'] = encoder.fit_transform(target) data[‘Sex'].unique()
# output:array([0, 1, 2], dtype=int64)
4 其他处理
4.1 利用value_counts函数查看每个类别数量
pd.Series(data['Species']).value_counts()

可以看到,数据集中种类是Adelie Penguin (Pygoscelis adeliae)、Chinstrap penguin (Pygoscelis antarctica)、Gentoo penguin (Pygoscelis papua)的企鹅分别有152、124、68个。
4.2 特征与标签组合的散点可视化
sns.pairplot(data=data, diag_kind='hist', hue= 'Species')
plt.show()
二、机器学习算法
经过数据预处理的数据比较完整可靠,下面我们将处理后的数据应用到算法中。
1 数据归一化和划分
1.1 数据归一化处理
for i in list(['Culmen Length (mm)','Culmen Depth (mm)','Flipper Length (mm)','Body Mass (g)']):
Max=np.max(data[i])
Min=np.min(data[i])
data[i]=(data[i]-Min)/(Max-Min)
1.2 数据集划分
为了正确评估模型性能,将数据划分为训练集和测试集,并在训练集上训练模型,在测试集上验证模型性能,我们将训练集和测试集划分为4:1。
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(data[['Culmen Length (mm)','Culmen Depth (mm)', 'Flipper Length (mm)','Body Mass (g)', ‘Sex’]], data[['Species']], test_size = 0.2, random_state = 2022)
2 算法应用
以决策树为例,sklearn的tree模块提供了 DecisionTreeClassifier 算法的具体实现。
2.1 算法实现
## 从sklearn中导入决策树模型
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
from sklearn import metrics
## 定义 决策树模型
clf = DecisionTreeClassifier()
# 在训练集上训练决策树模型
clf.fit(x_train, y_train)
## 在训练集和测试集上分布利用训练好的模型进行预测
train_predict = clf.predict(x_train)
test_predict = clf.predict(x_test)
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict))
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))
## 由于决策树模型是概率预测模型(前文介绍的 p = p(y=1|x,\theta)),所有我们可以利用 predict_proba 函数预测其概率
train_predict_proba = clf.predict_proba(x_train)
test_predict_proba = clf.predict_proba(x_test)
# print('The test predict Probability of each class:\n',test_predict_proba)
## 其中第一列代表预测为0类的概率,第二列代表预测为1类的概率,第三列代表预测为2类的概率。
## 利用accuracy(准确度)【预测正确的样本数目占总预测样本数目的比例】评估模型效果
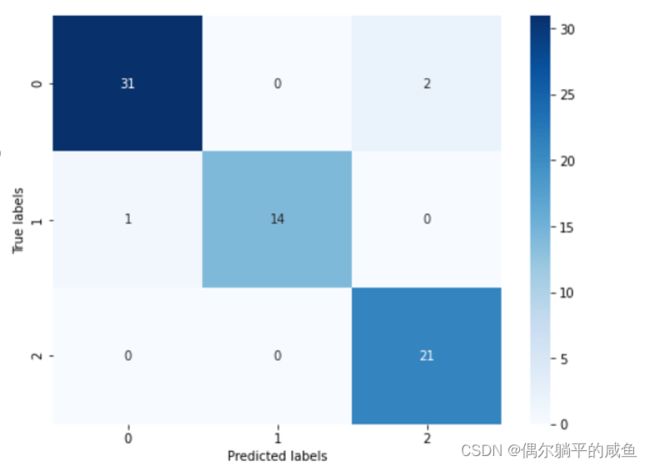
## 查看混淆矩阵
confusion_matrix_result = metrics.confusion_matrix(test_predict,y_test)
print('The confusion matrix result:\n',confusion_matrix_result)
# 利用热力图对于结果进行可视化
plt.figure(figsize=(8, 6))
sns.heatmap(confusion_matrix_result, annot=True, cmap='Blues')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()
2.2 算法评估与分析
2.2.1 模型特征重要性andPermutation Importance
注意!不是所有的模型都有feature_importances_属性
from sklearn.inspection import permutation_importance
fearture_name=['Culmen Length (mm)','Culmen Depth (mm)', 'Flipper Length (mm)','Body Mass (g)']
feature_importance = clf.feature_importances_
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + 0.5
fig = plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.barh(pos, feature_importance[sorted_idx], align="center")
plt.yticks(pos, np.array(fearture_name)[sorted_idx])
plt.title("Feature Importance (MDI)")
result = permutation_importance(
clf, x_test, y_test, n_repeats=15, random_state=12, n_jobs=1
)
# print(result)
sorted_idx = result.importances_mean.argsort()
plt.subplot(1, 2, 2)
plt.boxplot(
result.importances[sorted_idx].T,
vert=False,
labels=np.array(fearture_name)[sorted_idx],
)
plt.title("Permutation Importance (test set)")
fig.tight_layout()
plt.show()
2.2.2 提取特征可视化
from matplotlib.colors import ListedColormap
# 使用两个特征来预测,这样方便绘制预测结果
x = data[['Culmen Length (mm)','Culmen Depth (mm)']]
y = data['Species']
clf =GradientBoostingClassifier()
clf.fit(x, y)
# 创建颜色组合
cmap_light = ListedColormap(['orange', 'cyan', 'cornflowerblue'])
cmap_bold = ['darkorange', 'c', 'darkblue']
# 绘制不同类别区域
x_min, x_max = x[ 'Culmen Length (mm)'].min() - 1, x['Culmen Length (mm)'].max() + 1
y_min, y_max = x['Culmen Depth (mm)'].min() - 1, x['Culmen Depth (mm)'].max() + 1
h = .02
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
plt.contourf(xx, yy, z, cmap=cmap_light)
# 绘制数据点
sns.scatterplot(x=x['Culmen Length (mm)'], y=x['Culmen Depth (mm)'], hue=y,
palette=cmap_bold, alpha=1.0, edgecolor="black")
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xlabel('Culmen Length (mm)')
plt.ylabel('Culmen Depth (mm)')
plt.title('GradientBoostingClassifier-liliangshuo-210217')
plt.show()
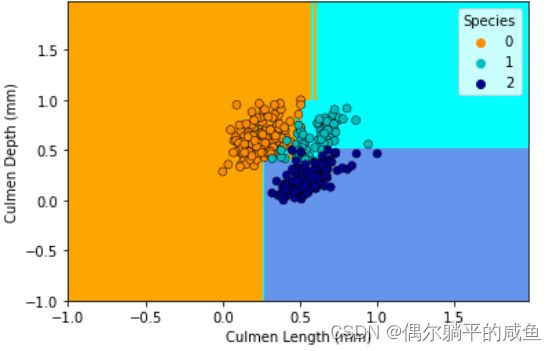
使用前两个特征来预测,这样方便绘制预测结果。可以看出,0和2分类的比较准确,而1相对来说不准确,符合我们的决策树分类模型预测的结果。
3 其他常用机器学习算法的封装(分类)
①逻辑回归模型
from sklearn.linear_model import LogisticRegression
②支持向量机分类
from sklearn.svm import SVC()
③MLP分类
from sklearn.neural_network import MLPClassifier
④KNN分类
from sklearn.neighbors import KNeighborsClassifier
⑤决策树分类
from sklearn.tree import DecisionTreeClassifier
⑥梯度提升决策树分类
from sklearn.ensemble import GradientBoostingClassifier
⑦随机森林分类
from sklearn.ensemble import RandomForestClassifier