第11章 特征选择与稀疏学习
第11章 特征选择与稀疏学习
11.1 子集搜索与评价
特征:属性
相关特征(relevant feature):对当前学习任务有用的属性
特征选择(feature selection):从给定的特征集合中选择出相关特征子集的过程
特征选择的原因
1、维数灾难问题
2、去除不相关特征往往会降低学习任务的难度
特征选择过程必须确保不丢失重要特征,否则后续学习过程会因为重要信息的缺失而无法获得好的性能。
子集搜索(subset search):给定特征集合 { a 1 , a 2 , … , a d } \left\{ a_{1},a_{2},\ldots,a_{d} \right\} {a1,a2,…,ad},将每个特征看作一个候选子集,对这d个候选单特征子集进行评价,假定 { a 2 } \left\{ a_{2} \right\} {a2}最优,于是将 { a 2 } \left\{ a_{2}\right\} {a2}作为第一轮的选定集;然后在上一轮的选定集中加入一个特征,构成包含两个特征的候选子集,假定在这 d − 1 d- 1 d−1个候选两特征子集 { a 2 , a 4 } \left\{ a_{2},a_{4} \right\} {a2,a4}中最优,且优于 { a 2 } \left\{a_{2} \right\} {a2},于是将 { a 2 , a 4 } \left\{ a_{2},a_{4} \right\} {a2,a4}作为本轮的选定集;……假定在第 k + 1 k + 1 k+1轮时,最优的候选 ( k + 1 ) \left( k + 1\right) (k+1)特征子集不如上一轮的选定集,则停止生成候选子集,并将上一轮选定的k特征集合作为选择结果。
前向(forward)搜索:若从一个特征子集开始,每次逐渐增加相关特征
后向(backward)搜索:若从完整的特征集合开始,每次场所去掉一个无关特征这样逐渐减少特征
双向(bidirectional)搜索:将前向和后向搜索结合,每一轮逐渐增加选定相关特征,同时减少无关特征
子集评价(subset evaluation):给定数据集D,假定D中第i类样本所占的比例为 p i ( i = 1 , 2 , … , ∣ y ∣ ) p_{i}\left( i =1,2,\ldots,\left| y \right|\right) pi(i=1,2,…,∣y∣)。假定样本属性均为离散型,对属性子集A,假定根据其取值将D分成了V个子集 { D 1 , D 2 , … , D V } \left\{D^{1},D^{2},\ldots,D^{V}\right\} {D1,D2,…,DV},每个子集中的样本在A上取值相同,则属性子集A的信息增益:
Gain ( A ) = E n t ( D ) − ∑ v = 1 V ∣ D v ∣ D Ent ( D v ) \text{Gain}\left( A \right) = Ent\left( D \right) - \sum_{v = 1}^{V}\frac{\left| D^{v} \right|}{D}\text{Ent}\left( D^{v} \right) Gain(A)=Ent(D)−v=1∑VD∣Dv∣Ent(Dv)
其中信息熵定义为
Ent ( D ) = − ∑ k = 1 ∣ y ∣ p k p k \text{Ent}\left( D \right) = - \sum_{k = 1}^{\left| y \right|}{p_{k}\operatorname{}p_{k}} Ent(D)=−k=1∑∣y∣pkpk
信息增益 Gain ( A ) \text{Gain}\left( A\right) Gain(A)越大,意味着特征子集A包含的有助于分类的信息越多
特征选择方法:过滤式(filter)、包裹式(wrapper)和嵌入式(embedding)
11.2 过滤式选择
过滤式方法先用特征选择过程对初始特征进行过滤,在用过滤的特征来训练模型
Relief方法设计了一个相关统计量来度量特征的重要性。该统计量时一个向量,其每个分量分别对应于一个初始特征,而特征子集的重要性则是由子集中每个特征所对应的相关统计量分量之和来决定。指定一个阈值 τ \tau τ,然后选择比 τ \tau τ大的相关统计量分量所对应的特征;或者指定欲选取的特征个数k,然后选择相关统计量分量最大的k个特征。
猜中近邻(near-hit):给定训练集 { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) } \left\{ \left( x_{1},y_{1} \right),\left(x_{2},y_{2}\right),\ldots,\left( x_{m},y_{m} \right) \right\} {(x1,y1),(x2,y2),…,(xm,ym)},对每个示例 x i x_{i} xi,Relief先在 x i x_{i} xi的同类样本中寻找其最近邻 x i , n h x_{i,nh} xi,nh
猜错近邻(near-miss):再从 x i x_{i} xi的异类样本中寻找其最近邻 x i , n m x_{i,nm} xi,nm
相关统计量对应于属性j的分量为
δ j = ∑ i − d i f f ( x i j , x i , n h j ) 2 + d i f f ( x i j , x i , n m j ) 2 \delta^{j} = \sum_{i}^{}{- diff\left( x_{i}^{j},x_{i,nh}^{j} \right)^{2} + diff\left( x_{i}^{j},x_{i,nm}^{j} \right)^{2}} δj=i∑−diff(xij,xi,nhj)2+diff(xij,xi,nmj)2
其中 x a j x_{a}^{j} xaj表示样本 x a x_{a} xa在属性j上的取值, diff ( x a j , x b j ) 2 \text{diff}\left( x_{a}^{j},x_{b}^{j}\right)^{2} diff(xaj,xbj)2取决于属性j的类型:若属性j为离散型,则 x a j = x b j x_{a}^{j} = x_{b}^{j} xaj=xbj时 diff ( x a j , x b j ) 2 = 0 \text{diff}\left( x_{a}^{j},x_{b}^{j} \right)^{2} = 0 diff(xaj,xbj)2=0,否则为1;若j为连续型,则 diff ( x a j , x b j ) 2 = ∣ x a j − x b j ∣ \text{diff}\left( x_{a}^{j},x_{b}^{j} \right)^{2} = \left| x_{a}^{j} - x_{b}^{j}\right| diff(xaj,xbj)2=∣∣∣xaj−xbj∣∣∣,注意 x a j , x b j x_{a}^{j},x_{b}^{j} xaj,xbj已规范化到[0,1]区间
Relief其扩展变体Relief-F能处理多分类问题,则相关统计量对应于属性j的分量为
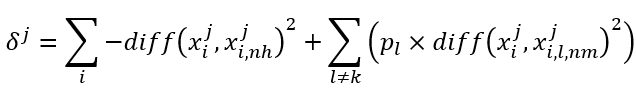
其中 p l p_{l} pl为第l类样本在数据集D中所占的比例。
11.3 包裹式选择
包裹式特征选择的目的就是为给定学习器选择最利于其性能、量身定做的特征子集。
LVW(Las Vegas Wrapper)在拉斯维加斯方法(Las Vegas method)框架下使用随机策略进行子集搜索,并以最终分类器的误差为特征子集评价准则。

11.4 嵌入式选择与 L 1 \mathbf{L}_{\mathbf{1}} L1正则化
嵌入式特征选择是将特征选择过程与学习器训练过程融为一体,两者在同一个优化过程中完成,即在学习器训练过程中自动地进行了特征选择。
L 1 L_{1} L1范数和 L 2 L_{2} L2范数正则化都有助于降低过拟合风险,但前者还会带来一个额外的好处:它比后者更易于获得稀疏解
L 1 L_{1} L1正则化问题的求解可使用近端梯度下降(Proximal Gradient Descent,PGD)。令 ∇ \nabla ∇表示微分算子,对优化目标
![]()
若 f ( x ) f\left( x \right) f(x)可导,且 ∇ f \nabla f ∇f满足L-Lipschits条件,即存在常数 L > 0 L > 0 L>0使得
∥ ∇ f ( x ′ ) − ∇ f ( x ) ∥ 2 2 ≤ L ∥ x ′ − x ∥ 2 2 ( ∀ x , x ′ ) \left\| \nabla f\left( x' \right) - \nabla f\left( x \right) \right\|_{2}^{2} \leq L\left\| x^{'} - x \right\|_{2}^{2}\left( \forall x,x' \right) ∥∇f(x′)−∇f(x)∥22≤L∥∥∥x′−x∥∥∥22(∀x,x′)
则在 x k x_{k} xk附近可将 f ( x ) f\left( x \right) f(x)通过二阶泰勒展式近似为
f ^ ( x ) ≃ f ( x k ) + ⟨ ∇ f ( x k ) , x − x k ⟩ + L 2 ∥ x − x k ∥ 2 = L 2 ∥ x − ( x k − 1 L ∇ f ( x k ) ) ∥ 2 2 + c o n s t \hat{f}\left( x \right) \simeq f\left( x_{k} \right) + \left\langle \nabla f\left( x_{k} \right),x - x_{k} \right\rangle + \frac{L}{2}\left\| x - x_{k} \right\|^{2} = \frac{L}{2}\left\| x - \left( x_{k} - \frac{1}{L}\nabla f\left( x_{k} \right) \right) \right\|_{2}^{2} + const f^(x)≃f(xk)+⟨∇f(xk),x−xk⟩+2L∥x−xk∥2=2L∥∥∥∥x−(xk−L1∇f(xk))∥∥∥∥22+const
其中const是与x无关的常数, ⟨ . , . ⟩ \left\langle .,.\right\rangle ⟨.,.⟩表示内积,则上式的最小值在 x k + 1 x_{k + 1} xk+1获得:

对于上式,可先求解 z = x k − 1 L ∇ f ( x k ) {z = x}_{k} - \frac{1}{L}\nabla f\left( x_{k}\right) z=xk−L1∇f(xk),然后求解
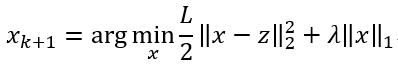
令 x i x^{i} xi表示x的第i个分量,将上式按分量展开,其中不存在 x i x j ( i ≠ j ) x^{i}x^{j}\left( i\neq j \right) xixj(i̸=j),则有闭式解:
x k + 1 i = { z i − λ L , λ L < z i 0 , ∣ z i ∣ ≤ λ L z i + λ L , z i < − λ L x_{k + 1}^{i} = \left\{ \begin{matrix}z^{i} - \frac{\lambda}{L},{\frac{\lambda}{L } <z^{i}} \\ 0,\left| z^{i} \right| \leq \frac{\lambda}{L} \\z^{i} + \frac{\lambda}{L},z^{i} < - \frac{\lambda}{L} \\\end{matrix} \right.\ xk+1i=⎩⎨⎧zi−Lλ,Lλ<zi0,∣∣zi∣∣≤Lλzi+Lλ,zi<−Lλ
其中 x k + 1 i x_{k + 1}^{i} xk+1i与 z i z^{i} zi分别是 x k + 1 x_{k + 1} xk+1和z的第i个分量
11.5 稀疏表示与字典学习
把数据集D考虑成一个矩阵,其每行对应于一个样本,每列对应于一个特征。矩阵中的许多列与单曲学习任务无关,通过特征选择去除这些列,则学习器训练过程近需在较小的矩阵上进行,学习任务的难度可能有所降低,涉及的计算和存储开销会减少,学得模型的可解释性也会提高。
字典学习(dictionary learning):亦称稀疏编码(sparse
coding),为普通稠密表达的样本找到合适的字典,将样本转化为合适的稀疏表示形式,从而使学习任务得以简化,模型复杂度得以降低。
给定数据集 { x 1 , x 2 , … , x m } \left\{ x_{1},x_{2},\ldots,x_{m} \right\} {x1,x2,…,xm},字典学习最简单的形式为
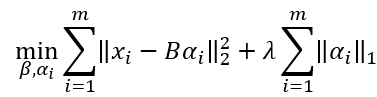
其中 B ∈ R d × k B \in \mathbb{R}^{d \times k} B∈Rd×k为字典矩阵,k称为字典的词汇量, α i ∈ R k \alpha_{i} \in \mathbb{R}^{k} αi∈Rk则是样本 x i ∈ R d x_{i} \in \mathbb{R}^{d} xi∈Rd的稀疏表示
固定字典B,其中不涉及交叉项 α i u α i v ( u ≠ v ) \alpha_{i}^{u}\alpha_{i}^{v}\left( u \neq v \right) αiuαiv(u̸=v),从而每个样本 x i x_{i} xi找到相应的 α i \alpha_{i} αi:
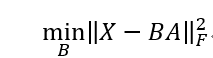
其中 X = ( x 1 , x 2 , … , x m ) ∈ R d × m , A = ( α 1 , α 2 , … , α m ) ∈ R k × m , ∥ . ∥ F X = \left( x_{1},x_{2},\ldots,x_{m} \right) \in \mathbb{R}^{d \times m},A = \left( \alpha_{1},\alpha_{2},\ldots,\alpha_{m} \right) \in \mathbb{R}^{k \times m},\left\| . \right\|_{F} X=(x1,x2,…,xm)∈Rd×m,A=(α1,α2,…,αm)∈Rk×m,∥.∥F是矩阵的Frobenius范数。
基于逐列更新策略的KSVD求解上式,令 b i b_{i} bi表示字典矩阵B的第i列, α i \alpha^{i} αi表示稀疏矩阵A的第i行,则

最小化上式只需对 E i E_{i} Ei进行奇异值分解以取得最大奇异值所对应的正交向量
11.6 压缩感知
假定有长度为m的离散信号x,假定以远小于奈奎斯特采样定理要求的采样率进行采样,得到长度为n的采样后信号有, n ≪ m n\ll m n≪m,即:
y = ϕ x y = \phi x y=ϕx
其中 ϕ ∈ R n × m \phi \in \mathbb{R}^{n \times m} ϕ∈Rn×m是对信号x的测量矩阵
假设存在某个线性变换 ψ ∈ R m × m \psi \in \mathbb{R}^{m \times m} ψ∈Rm×m,使得x可表示为 ψ s \psi s ψs,则
y = ϕ ψ s = A s y = \phi\psi s = As y=ϕψs=As
其中 A = ϕ ψ ∈ R n × m A = \phi\psi \in \mathbb{R}^{n \times m} A=ϕψ∈Rn×m
压缩感知分为感知测量和重构恢复
感知测量:对原始信号进行处理以获得稀疏样本表示
重构恢复:基于稀疏性从少量观测中恢复原信号。
限定等距性(Restricted Isometry Property, RIP)
对大小为 n × m ( n ≪ m ) n \times m\left( n \ll m \right) n×m(n≪m)的矩阵A,若存在常数 δ k ∈ ( 0 , 1 ) \delta_{k} \in \left( 0,1 \right) δk∈(0,1)使得对于任意向量s和A的所有子矩阵 A k ∈ R n × k A_{k} \in \mathbb{R}^{n \times k} Ak∈Rn×k有
( 1 − δ k ) ∥ s ∥ 2 2 ≤ ∥ A k s ∥ 2 2 ≤ ( 1 + δ k ) ∥ s ∥ 2 2 \left( 1 - \delta_{k} \right)\left\| s \right\|_{2}^{2} \leq \left\| A_{k}s \right\|_{2}^{2} \leq \left( 1 + \delta_{k} \right)\left\| s \right\|_{2}^{2} (1−δk)∥s∥22≤∥Aks∥22≤(1+δk)∥s∥22
则称A满足k限定等距性(k-RIP)。从y中恢复出稀疏信号s,进而恢复出x:
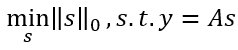
L 0 L_{0} L0范数最小化在一定条件下与 L 1 L_{1} L1范数最小化问题共解:
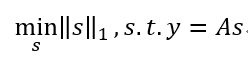
矩阵补全(matrix completion)技术
rank ( X ) , s . t . ( X ) ij = ( A ) ij , ( i , j ) ∈ Ω \operatorname{}{\text{rank}\left( X \right),s.t.\left( X \right)_{\text{ij}} = \left( A \right)_{\text{ij}},\left( i,j \right) \in \Omega} rank(X),s.t.(X)ij=(A)ij,(i,j)∈Ω
其中X表示需恢复的稀疏信号;rank(X)表示矩阵X的秩;A是已观测信号
rank(x)在集合 { X ∈ R m × n : ∥ X ∥ F 2 ≤ 1 } \left\{ X \in \mathbb{R}^{m \times n}:\left\| X \right\|_{F}^{2} \leq 1 \right\} {X∈Rm×n:∥X∥F2≤1}上的凸包X的核范数(nuclear norm):
∥ X ∥ ∗ = ∑ j = 1 min { m , n } σ j ( X ) \left\| X \right\|_{*} = \sum_{j = 1}^{\min\left\{ m,n \right\}}{\sigma_{j}\left( X \right)} ∥X∥∗=j=1∑min{m,n}σj(X)
其中 σ j ( X ) \sigma_{j}\left( X \right) σj(X)表示X的奇异值,则

通过半正定规划(Semi-Definite Programming, SDP)求解。