MATLAB数字图像去噪处理系统[GUI]
MATLAB数字图像去噪处理系统[GUI]
1、摘 要
现代图像、语声、数据通信对线性相位的要求是普遍的。正是此原因,使得具有线性相位的FIR数字滤波器得到大力发展和广泛应用。
在实际进行数字信号处理时,往往需要把信号的观察时间限制在一定的时间间隔内,只需要选择一段时间信号对其进行分析。取用有限个数据,即将信号数据截断的过程,就等于将信号进行加窗函数操作。这样操作以后,常常会发生频谱分量从其正常频谱扩展开来的现象,即所谓的“频谱泄漏”。当进行离散傅立叶变换时,时域中的截断是必需的,因此泄漏效应也是离散傅立叶变换所固有的,必须进行抑制。而要对频谱泄漏进行抑制,可以通过窗函数加权抑制DFT的等效滤波器的振幅特性的副瓣,或用窗函数加权使有限长度的输入信号周期延拓后在边界上尽量减少不连续程度的方法实现。
数字带通滤波器是一种用来过滤时间离散信号的数字系统,通过对抽样数据进行数学处理来达到频域滤波的目的。根据其单位重启响应函数的时域特性可分为两类:无限冲击响应滤波器(IIR),有限冲击响应滤波器(FIR)。与IIR滤波器相比,FIR的实现是递归的,总是稳定的;更重要的是,FIR滤波器在满足幅频响应要求的同时,可以获得严格的线性相位特性。因此,它在高保真的信号处理,如信号音频,图像处理,数据传输等领域得到广泛的应用。
数字fir滤波器的设计方法有很多种。如窗函数法设计,频率采样设计法和最优化设计法等。
参考链接【如链接无效,请留言提醒】
B小波图像去噪.zip-专业指导文档类资源-CSDN下载
2.编程及运行结果
2.1常见基本运算
2.1.1极限的计算
MATLAB提供的命令limit()可以完成极限运算,其调用格式如下: limit(F,x,a,'left')
该命令对表达式F求极限,独立变量x从左边趋近于a,函数中除F外的参数均可省略,'left'可换成'right'。
例:求极限S= [1+1/x]
代码如下:
clear;
F=sym('1+1/x')
limit(F,'x',inf,'left')
运行结果:
2.1.2微分的计算
MATLAB提供的函数diff()可以完成对给定函数求导函数的运算,其调用格式如下:diff(fun,x,n),其意义是求函数fun关于变量x的n阶导数,n为1时可省略。这里的fun用上例的后一种方式来定义较为妥当。
例:求函数y=log的一阶导。
代码如下:
clear;
syms x
y=log(1/x);
dy=diff(y,x)
运行结果:
2.1.3积分的计算
MATLAB中主要用int进行符号积分,用trapz,dblquad,quad,quad8等进行数值积分。
R=int(s,v)%对符号表达式中指定的符号变量v计算不定积分,表达式R只是表达式函数s的一个原函数,后面没有带任何常数C。
R=int(s)%对符号表达式s的确定的符号变量计算不定积分。
R=int(s,a,b)%符号表达式s的定积分,a,b分别为积分的上,下限。
trapz(x,y)梯形积分法,x时表示积分区间的离散化向量,y是与x同维数的向量,表示被积函数,z返回积分值。
fblquad(‘fun',a,b,c,d)矩形区域二重积分,fun表示被积函数的M函数名,a,b分别为x的上下限,c,d分别为y的上下线。
例1:(不定积分)用符号积分命令int计算
代码如下:
clear;
syms x
int(x^2*sin(x))
运行结果:
例2:(定积分)计算数值积分
①用符号积分命令int,代码如下:
clear;
syms x;
int(x^4,x,-2,2)
运行结果:
②改用梯形积分法命令trapz计算积分,代码如下:
clear;
x=-2:0.01:1;
y=x.^2;
trapz(x,y)
运行结果:
2.1.4级数的计算
MATLAB中主要用symsun,taylor求级数的和及Taylor展开。其中Symsum(s,v,a,b)表达式s关于变量v从a到b求和Taylor(f,a,n)将函数f在a点展开为n-1阶Taylor多项式
例:用Symsum计算
代码如下:
clear;clc;
syms x y
z=1/(x^3);
symsum(z,x,1,9)
运行结果:
2.1.5求解代数方程
MATLAB命令输人格式:solve('equ1','equ2',...'equN'),其中eqni表示第i个方程。
例1:求解方程 x^2+b*x+c=0
代码如下:
solve('a*x^2+b*x+c')
运行结果:
2.1.6求解常微分方程
MATLAB中主要用dsolve求符号解析解,ode45,ode23,ode15s求数值解。s=dsolve(‘方程1', ‘方程2',…,'初始条件1','初始条件2' …,'自变量') 用字符串方程表示,自变量缺省值为t。导数用D表示,2阶导数用D2表示,以此类推。S返回解析解。在方程组情形,s为一个符号结构。
[tout,yout]=ode45(‘yprime',[t0,tf],y0) 采用变步长四阶Runge-Kutta法和五阶Runge-Kutta-Felhberg法求数值解,yprime是用以表示f(t,y)的M文件名,t0表示自变量的初始值,tf表示自变量的终值,y0表示初始向量值。输出向量tout表示节点(t0,t1, …,tn)T,输出矩阵yout表示数值解,每一列对应y的一个分量。若无输出参数,则自动作出图形。
例:求解微分方程的特解
在初始条件下的特解:y(0)=1
代码如下:
dsolve('(x^2-1)*Dy+2*x*y-cos(x)=0','y(0)=1','x')
运行结果如下:
2.2 矩阵基本计算
2.2.1矩阵的最大值
求一个向量X的最大值的函数有两种调用格式,分别是:
(1) y=max(X):返回向量X的最大值存入y,如果X中包含复数元素,则按模取最大值。
(2) [y,I]=max(X):返回向量X的最大值存入y,最大值的序号存入I,如果X中包含复数元素,则按模取最大值。
例:求出矩阵[12,52,-25,63,45,1,0,12]中的最大值及其所在位置
代码如下:
x=[12,52,-25,63,45,1,0,12];
[y,l]=max(x) %求向量x中的最大值及其该元素的位置
运行结果:
2.2.2矩阵的最小值
求一个向量X的最小值的函数有两种调用格式,分别是:
(1) y=min(X):返回向量X的最小值存入y,如果X中包含复数元素,则按模取最大值。
(2) [y,I]=min (X):返回向量X的最小值存入y,最小值的序号存入I,如果X中包含复数元素,则按模取最小值。
例:求出矩阵[-5,85,74,42,-2,3,0,-568]中的最小值及其所在位置
代码如下:
x=[-5,85,74,42,-2,3,0,-568];
[y,l]=min(x) %求向量x中的最小值及其该元素的位置
运行结果:
2.2.3矩阵的均值
mean(A,1)表示对列取平均,mean(A,2)表示对行取平均,mean(A)则默认为mean(A,1)
例:求[45,47,41,42,46,48,42,45,44]均值
代码如下:
A=[45,47,41;42,46,48;42,45,44]
mean(A,1)
mean(A,2)
运行结果如下:
2.2.4矩阵的方差
var(a); % 默认来求
var(a, 0); % 默认的公式(用N-1)
var(a, 1); % 另外的公式(用N)
var(a, 0, 1); % 对每列操作
var(a, 0, 2); % 对每行操作
var(a'); % 检验
var(a(:)); % 通过直接访问矩阵的存储,来对矩阵进行操作
例:求方差
代码如下:
a=rand(3,4) %(0,1)之间产生随机数
b=var(a)
c=var(a(:))
运行结果:
2.2.5矩阵的转置
矩阵转置用符号“`”来表示和实现, 如故Z是复数矩阵,则Z`为它们的复数共轭转置矩阵,非共轭转置矩阵使用Z.`或conj(Z`)。
例:求[33,34,33,36;32,33,31,33;38,37,30,37;34,36,37,34]的转置。
代码如下:
A=[33,34,33,36;32,33,31,33;38,37,30,37;34,36,37,34]
B=A'
运行结果:
2.2.6矩阵的逆
MATLAB中求矩阵的逆用函数inv(A)
例:求矩阵A=[13,14,15,16;12,13,11,13;18,17,10,17;14,16,17,14]的逆
代码如下:
A=[13,14,15,16;12,13,11,13;18,17,10,17;14,16,17,14]
B=inv(A)
运行结果:
2.2.7矩阵的行列式
调用函数det格式:d = det(X)
例:求矩阵[13,4,1,2;1,2,1,3;8,7,2,7;14,6,7,1]的行列式
代码如下:
A=[13,4,1,2;1,2,1,3;8,7,2,7;14,6,7,1]
B=det(A)
运行结果:
2.2.8矩阵的特征值计算
MATLAB中用函数eig()来进行求特征值和特征向量,其调用格式如下:d=eig(A),返回矩阵A的所有特征值。
[V,D] = eig(A),返回矩阵A 的特征值和特征向量,它们满足如下关系:A*V = V*D。
[V,D] = eig( A ,'nobalance') ,在求解特征值和特征向量时不采用初期的平衡步骤。一般来说平衡步骤对输入矩阵进行调整,这使得计算出的特征值和特征向量更加准确。然而如果输入矩阵中确实含有值很小的元素(可能会导致截断误差),平衡步骤有可能加大这种误差,从而得到错误的特征值和特征向量。
d = eig(A,B),返回矩阵A 和B 的广义特征值。
[V,D] = eig(A,B),返回矩阵A 和B 的广义特征值和广义特征向量。
[ V,D] = eig( A,B,flag),flag 有'chol'和‘qz' 两种值。当flag ='chol' 时,计算广义特征值采用B 的Cholesky 分解来实现。当flag ='qz'时,无论矩阵的对称性如何,都采用QZ算法来求解广义特征值。
例:求矩阵[33,24,15,26;12,23,31,33;38,27,20,37;14,16,22,14]的特征值和特征向量
代码如下:
A=[33,24,15,26;12,23,31,33;38,27,20,37;14,16,22,14]
[V D]=eig(A)
eig(A)
运行结果:
2.2.9矩阵的相乘
例:求[1,2,3,4;5,6,7,8;9,1,2,3]和[2;3;6;7]的乘积。
代码如下:
A=[1,2,3,4;5,6,7,8;9,1,2,3]
B=[2;3;6;7]
C=A*B
运行结果:
2.2.10矩阵的右除和左除
MATLAB中左除和右除分别用“\”和“/”表示
例:求[11,12,13;14,15,16;17,18,19]和[15,14,16;17,16,18;12,14,19]的左除和右除
代码如下:
A=[11,12,13;14,15,16;17,18,19];
B=[15,14,16;17,16,18;12,14,19];
C=A\B
D=A/B
运行结果:
2.2.11矩阵的幂运算
例:求矩阵[1,2,3,4;5,6,7,8;7,5,4,3]的3次幂
代码如下:
A=[1,2,3,4;5,6,7,8;7,5,4,3;4,5,6,7]
B=3;
C=A^B
运行结果:
2.3 多项式基本计算
2.3.1多项式加减运算
例:计算[31,12,13,16,87]和[5,9,6,6,3]的加减乘除
编程如下:
A=[31,12,13,16,87];
B=[5,9,6,6,3];
C=A+B
D=A-B
运行结果:
2.3.2多项式乘除运算
conv(A,B)用于多项式的乘法;
Decnov(A,B)用于多项式相除求余式。
例:
P1=[3,4,4,2,3,4,5]
P2=[6,7,8]
P=conv(P1,P2)
P3=deconv(P,P1)
运行结果:
2.3.3多项式求导
polyder(P) %对多项式P进行微分运算
例:
代码如下
P=[1,2,3,4,5]
P1=poly2sym(P)
Q=polyder(P)
运行结果如下:
2.3.4求根和求值运算
polyval(P) %按数组计算规则计算多项式P的值
polyvalm(P) %按矩阵计算规则计算多项式P的值
例:求多项式
在x=2.5时的值。
代码如下:
P=[1,4,4]
Pv=polyval(P,0.5)
运行结果:
2.3.5多项式的部分分式展开
调用函数residue格式:[r,p,k] = residue(b,a),[b,a] = residue(r,p,k)
其中,b与a分别为两个多项式。其中a为分式之分母,b该分式之分子,两者均为向量型式;而[r,p,k]等则为行向量,分别代表展开后之分子、分母及余数之系数,若能除尽则k项应为零。r与p分别为余数与极数,其个数应相等,但应比a之个数少一。
代码如下:
b=[3,4,5];
a=[8,-6,3];
[r,p,k]=residue(b,a)
运行结果:
2.3.6多项式的拟合
MATLAB软件提供了基本的曲线拟合函数的命令.多项式函数拟合:a=polyfit(xdata,ydata,n)其中n表示多项式的最高阶数,xdata,ydata为将要拟合的数据,它是用数组的方式输入.输出参数a为拟合多项式 y=a1xn+...+anx+a n+1的系数
例:已知五个数据点:[1,5.5],[2,4.3],[3,12.8],[4,2.9],[5,4.98],试画出这五个点拟合的三次曲线。
代码如下:
x=[1,2,3,4,5];y=[5.5,4.3,1.28,0.29,0.498];
p=polyfit(x,y,3)
x2=1:0.1:5;y2=polyval(p,x2);
plot(x,y,'o',x2,y2) ,grid on
运行结果:
2.3.7插值运算
yi = interp1(x,Y,xi,method) %用指定的算法计算插值:
'nearest':最近邻点插值,直接完成计算;
'linear':线性插值(缺省方式),直接完成计算;
'spline':三次样条函数插值。
'cubic': 分段三次Hermite插值。
对于超出x范围的xi的分量,使用方法'nearest'、'linear'、'v5cubic'的插值算法,相应地将返回NaN。对其他的方法,interp1将对超出的分量执行外插值算法。
yi = interp1(x,Y,xi,method,'extrap')
yi = interp1(x,Y,xi,method,extrapval) %确定超出x范围的xi中的分量的外插值extrapval,其值通常取NaN或0。
ZI = interp2(X,Y,Z,XI,YI,method) %用指定的算法method计算二维插值:
'linear':双线性插值算法(缺省算法);
'nearest':最临近插值;
'spline':三次样条插值;
'cubic':双三次插值。
例:用二维三次插值函数模拟函数z(x,y)=sin(x)+cos(y)。
代码如下:
clear;
clc;
x=linspace(0,2*pi,6);
y=linspace(0,2*pi,6);
[X,Y]=meshgrid(x,y);
Z=cos(X)+sin(Y);
surf(X,Y,Z)
x1=linspace(0,2*pi,36);
y1=x1;
[X1,Y1]=meshgrid(x1,y1);
Z1=interp2(X,Y,Z,X1,Y1,'cubic');
figure(2)
surf(X1,Y1,Z1)
运行结果:
3.基于MATLAB的图像滤波设计
3.1读入图像并分别加入高斯噪声、椒盐噪声和乘性噪声,并比较结果
函数使用imnoise函数进行图片的噪声加入,其调用格式如下:
J=imnoise(I,type,parameters)其中,type是噪声的类型,有高斯噪声,椒盐噪声,乘性噪声。类型名分别为:guassian,salt & pepper,speckle,parameters可表示噪声密度D。
代码如下:
clear;
I=imread('C:\Documents and Settings\Administrator\桌面\花.jpg');
subplot(2,2,1);
imshow(I);
title('原始图像');
J2=imnoise(I,'gaussian',0.1);
subplot(2,2,3)
imshow(J2)
title('高斯噪声图像');
J1=imnoise(I,'salt & pepper',0.1);
subplot(2,2,2)
imshow(J1)
title('椒盐噪声图像');
J3=imnoise(I,'speckle',0.1);
subplot(2,2,4)
imshow(J3)
title('乘性噪声图像');
运行结果,对比如下:
噪声密度D不同对图像干扰程度对比,程序如下:
高斯噪声:
clear;
I=imread('C:\Documents and Settings\Administrator\桌面\花.jpg');
J1=imnoise(I,'gaussian',0.03);
subplot(1,3,1);
imshow(J1);
title('d=0.03时的图像');
J2=imnoise(I,'gaussian',0.15);
subplot(1,3,2)
imshow(J2)
title('d=0.15时的图像');
J3=imnoise(I,'gaussian',0.5);
subplot(1,3,3)
imshow(J3)
title('d=0.5时的图像');
运行结果对比如下:
椒盐噪声:
clear;
I=imread('C:\Documents and Settings\Administrator\桌面\花.jpg');
J1=imnoise(I,'salt & pepper',0.03);
subplot(1,3,1);
imshow(J1);
title('d=0.03时的图像');
J2=imnoise(I,'salt & pepper',0.15);
subplot(1,3,2)
imshow(J2)
title('d=0.15时的图像');
J3=imnoise(I,'salt & pepper',0.5);
subplot(1,3,3)
imshow(J3)
title('d=0.5时的图像');
运行结果对比如下:
乘法噪声:
I=imread('C:\Documents and Settings\Administrator\桌面\花.jpg');
J1=imnoise(I,'speckle',0.03);
subplot(1,3,1);
imshow(J1);
title('d=0.03时的图像');
J2=imnoise(I,'speckle',0.15);
subplot(1,3,2)
imshow(J2)
title('d=0.15时的图像');
J3=imnoise(I,'speckle',0.5);
subplot(1,3,3)
imshow(J3)
title('d=0.5时的图像');
运行结果对比如下:
3.2设计巴特沃斯低通滤波对图像进行低通滤波处理,显示结果
巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦,没有起伏,而在阻频带则逐渐下降为零。 在振幅的对数对角频率的波得图上,从某一边界角频率开始,振幅随着角频率的增加而逐步减少,趋向负无穷大。
3.2.1叠加椒盐噪声的巴特沃斯低通滤波
i=imread('C:\Documents and Settings\Administrator\桌面\花.jpg'); I=rgb2gray(i);
I1=imnoise(I,'salt & pepper',0.02);
f=double(I1);
g=fft2(f);
g=fftshift(g);
[N1,N2]=size(g);
n=3; %阶次设为3
d0=100; %此处d0为截止频率
n1=fix(N1/2);
n2=fix(N2/2);
for i=1:N1
for j=1:N2
d=sqrt((i-n1)^2+(j-n2)^2);
h=1/(1+0.414*(d/d0)^(2*n));
result(i,j)=h*g(i,j);
end
end
result=ifftshift(result);
subplot(1,2,1),imshow(I1);
title('受椒盐噪声污染的图像');
subplot(1,2,2),imshow(J1);
title('截止频率为100HZ的巴特沃斯低通滤波处理后');
运行结果:
3.2.2叠加高斯噪声的巴特沃斯低通滤波
clear;
i=imread('C:\Documents and Settings\Administrator\桌面\花.jpg'); I=rgb2gray(i);
I1=imnoise(I,'gaussian',0.02);
f=double(I1);
g=fft2(f);
g=fftshift(g);
[N1,N2]=size(g);
n=3; %阶次设为3
d0=100; %此处d0为截止频率
n1=fix(N1/2);
n2=fix(N2/2);
for i=1:N1
for j=1:N2
d=sqrt((i-n1)^2+(j-n2)^2);
h=1/(1+0.414*(d/d0)^(2*n));
result(i,j)=h*g(i,j);
end
end
result=ifftshift(result);
subplot(1,2,1),imshow(I1);
title('受高斯噪声污染的图像');
subplot(1,2,2),imshow(J1);
title('截止频率为100HZ的巴特沃斯低通滤波处理后');
运行结果:
3.2.3叠加乘性噪声的巴特沃斯低通滤波
clear;
i=imread('C:\Documents and Settings\Administrator\桌面\花.jpg'); I=rgb2gray(i);
I1=imnoise(I,'speckle',0.02);
f=double(I1);
g=fft2(f);
g=fftshift(g);
[N1,N2]=size(g);
n=3; %阶次设为3
d0=100; %此处d0为截止频率
n1=fix(N1/2);
n2=fix(N2/2);
for i=1:N1
for j=1:N2
d=sqrt((i-n1)^2+(j-n2)^2);
h=1/(1+0.414*(d/d0)^(2*n));
result(i,j)=h*g(i,j);
end
end
result=ifftshift(result);
J1=uint8(real(X2));
subplot(1,2,1),imshow(I1);
title('受乘性噪声污染的图像');
subplot(1,2,2),imshow(J1);
title('截止频率为100HZ的巴特沃斯低通滤波处理后');
运行结果:
3.3用MATLAB实现高斯高通滤波器对图像的处理
I1=imread('C:\Documents and Settings\Administrator\桌面\花.jpg');
subplot(1,2,1);
imshow(I1);
title('原图');
f=double(I1);
g=fft2(f);
g=fftshift(g);
[M,N]=size(g);
d0=100;
m=fix(M/2); n=fix(N/2);
result=g;
for i=1:M
for j=1:N
d=sqrt((i-m)^2+(j-n)^2);
end
end
result=ifftshift(result);
J1=ifft2(result);
J2=uint8(real(J1));
subplot(1,2,2);
imshow(J2);
title('高斯高通滤波(d0=100)');
运行结果:
3.4维纳滤波和中值滤波对图像进行处理
随机信号或随机过程(random process)是普遍存在的。一方面,任何确定性信号经过测量后往往就会引入随机性误差而使该信号随机化;另一方面,任何信号本身都存在随机干扰,通常把对信号或系统功能起干扰作用的随机信号称之为噪声。噪声按功率谱密度划分可以分为白噪声(white noise)和色噪声(color noise),我们把均值为0的白噪声叫纯随机信号(pure random signal)。因此,任何其它随机信号都可看成是纯随机信号与确定性信号并存的混合随机信号或简称为随机信号。要区别干扰(interference)和噪声( noise)两种事实和两个概念。非目标信号(nonobjective signal)都可叫干扰。干扰可以是确定信号,如国内的50Hz工频干扰。干扰也可以是噪声,纯随机信号(白噪声)加上一个直流成分(确定性信号),就成了最简单的混合随机信号。医学数字信号处理的目的是要提取包含在随机信号中的确定成分,并探求它与生理、病理过程的关系,为医学决策提供一定的依据。例如从自发脑电中提取诱发脑电信号,就是把自发脑电看成是干扰信号,从中提取出需要的信息成分。因此我们需要寻找一种最佳线性滤波器,当信号和干扰以及随机噪声同时输入该滤波器时,在输出端能将信号尽可能精确地表现出来。
维纳滤波和卡尔曼滤波就是用来解决这样一类问题的方法:从噪声中提取出有用的信号。实际上,这种线性滤波方法也被看成是一种估计问题或者线性预测问题。对于在C中的图片而言,其进行均值滤波和维纳滤波的MATLAB的命令如下:
i=imread('C:\Documents and Settings\Administrator\桌面\花.jpg');
I=rgb2gray(i);
J1=imnoise(I,'gaussian',0,0.1); %高斯噪声 均值0 方差为0.1
subplot(2,3,4),imshow(K1,[]),title('对高斯噪声图像中值滤波');
K2=medfilt2(J2,[3,3]);
subplot(2,3,2),imshow(J2),title('椒盐噪声');
subplot(2,3,5),imshow(K2,[]),title('对椒盐噪声图像中值滤波');
K3=medfilt2(J3,[3,3]);
subplot(2,3,3),imshow(J3),title('乘性噪声');
subplot(2,3,6),imshow(K3,[]),title('对乘性噪声图像中值滤波');
运行结果:
以前面经常用的图片为例,再进行维纳滤波:
代码如下:
i=imread('C:\Documents and Settings\Administrator\桌面\花.jpg');
I=rgb2gray(i);
subplot(2,4,1),imshow(I); title('原始图像');
J1=imnoise(I,'gaussian',0,0.005);
subplot(2,4,2),imshow(J1);
title('高斯噪声图像');
K1=wiener2(J1);
subplot(2,4,6),imshow(K1);
title('维纳滤波');
J2=imnoise(I,'salt & pepper',0.005);
subplot(2,4,3),imshow(J2);
title('椒盐噪声图像');
subplot(2,4,7),imshow(K2);
title('维纳滤波');
J3=imnoise(I,'speckle',0.005);
subplot(2,4,4),imshow(J3);
title('乘性噪声图像');
K3=wiener2(J3);
subplot(2,4,8),imshow(K3);
title('维纳滤波');
运行结果:
参考文献
[1] 刘泉 《数字信号处理原理与实现》 电子工业出版社
[2] 刘泉 《信号与系统》 高等教育出版社
[3] 周博等编《MATLAB科学计算》 机械工业出版社
[4] 贺兴华等著.《MATLAB7.X图像处理》 人民邮电出版社
[5] 王洪元主编.《MATLAB语言以及在电子信息工程中的应用》 清华出版社.
[6] 张汗灵. 《MATLAB在图像处理中的应用》 清华大学出版社
[7] 董霖编 《MATLAB使用详解——基础、开发及工程应用》电子工业出版社
[8] Edward W.Kamen.《应用Web和MATLAB的信号与系统基础》.电子工业出版社

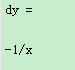
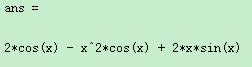
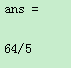
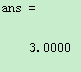
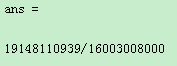


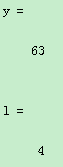
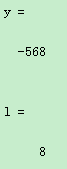
![MATLAB数字图像去噪处理系统[GUI]_第1张图片](http://img.e-com-net.com/image/info8/38273c08b5704796ab64739ab2ede793.png)
![MATLAB数字图像去噪处理系统[GUI]_第2张图片](http://img.e-com-net.com/image/info8/e298128d46eb49c6bbebaa4d6be24557.png)
![MATLAB数字图像去噪处理系统[GUI]_第3张图片](http://img.e-com-net.com/image/info8/eba837f0fa0e474b936035eb5df41ca9.png)
![MATLAB数字图像去噪处理系统[GUI]_第4张图片](http://img.e-com-net.com/image/info8/7dc948a47b314078a62bd35db502b17b.png)
![MATLAB数字图像去噪处理系统[GUI]_第5张图片](http://img.e-com-net.com/image/info8/e6c66e3cb4b941d0a80f46cff90cdfbf.png)
![MATLAB数字图像去噪处理系统[GUI]_第6张图片](http://img.e-com-net.com/image/info8/d637327e070843f18416f0d17beff539.png)
![MATLAB数字图像去噪处理系统[GUI]_第7张图片](http://img.e-com-net.com/image/info8/d1324f33bff7431fb60fcb4ee93bed54.png)
![MATLAB数字图像去噪处理系统[GUI]_第8张图片](http://img.e-com-net.com/image/info8/29e125641d4f46888a345d94bc5d3ff6.png)
![MATLAB数字图像去噪处理系统[GUI]_第9张图片](http://img.e-com-net.com/image/info8/d05d5e0b0add4fc2be72a6f26711c60e.png)
![MATLAB数字图像去噪处理系统[GUI]_第10张图片](http://img.e-com-net.com/image/info8/305729eafa264ac2bcc3d8adf8413e9f.png)
![MATLAB数字图像去噪处理系统[GUI]_第11张图片](http://img.e-com-net.com/image/info8/9be832a0e5334d7189924288909d22d7.png)
![MATLAB数字图像去噪处理系统[GUI]_第12张图片](http://img.e-com-net.com/image/info8/dfb41749126f47cda761337247e99fa3.png)
![MATLAB数字图像去噪处理系统[GUI]_第13张图片](http://img.e-com-net.com/image/info8/17b7f069bf474194af8c797f673e2b82.png)
![MATLAB数字图像去噪处理系统[GUI]_第14张图片](http://img.e-com-net.com/image/info8/64c11f6f04684b34b7ecff013b75116c.png)

![MATLAB数字图像去噪处理系统[GUI]_第15张图片](http://img.e-com-net.com/image/info8/5c1642cd77d14072b1233284e5cba2bd.jpg)
![MATLAB数字图像去噪处理系统[GUI]_第16张图片](http://img.e-com-net.com/image/info8/972bff732f484a24bbd77866d711358e.jpg)
![MATLAB数字图像去噪处理系统[GUI]_第17张图片](http://img.e-com-net.com/image/info8/1cce4a8255c641219c856de29a71d2c6.jpg)
![MATLAB数字图像去噪处理系统[GUI]_第18张图片](http://img.e-com-net.com/image/info8/0f051e5a13fd41568e7745c0681235a9.jpg)
![MATLAB数字图像去噪处理系统[GUI]_第19张图片](http://img.e-com-net.com/image/info8/7e894cadd6b84670aa9ac3090be3cf14.jpg)
![MATLAB数字图像去噪处理系统[GUI]_第20张图片](http://img.e-com-net.com/image/info8/f68c2c95f06b42a0ac85dc827b9ad4d1.jpg)
![MATLAB数字图像去噪处理系统[GUI]_第21张图片](http://img.e-com-net.com/image/info8/76941841043440c096223b9189718af2.jpg)
![MATLAB数字图像去噪处理系统[GUI]_第22张图片](http://img.e-com-net.com/image/info8/df391abe72aa4fc589f4ee56c5946977.jpg)
![MATLAB数字图像去噪处理系统[GUI]_第23张图片](http://img.e-com-net.com/image/info8/a5b27a46831a45f683832dc6ea3c410f.jpg)
![MATLAB数字图像去噪处理系统[GUI]_第24张图片](http://img.e-com-net.com/image/info8/47280d1c049a43b2a1a180f34dedac64.jpg)
![MATLAB数字图像去噪处理系统[GUI]_第25张图片](http://img.e-com-net.com/image/info8/7f9738c9686f49b3bc73b8244e76fed5.jpg)