萤火虫的小尾巴

[Python] 数据预处理(缺失值、异常值、重复值) [相关方法参数说明、代码示例、相关概念]

前言

系列文章目录
[Python]目录
视频及资料和课件
链接：https://pan.baidu.com/s/1LCv_qyWslwB-MYw56fjbDg?pwd=1234
提取码：1234

文章目录

前言

数据、文献

1. 缺失值处理

1.1 缺失值删除

1.1.1 适用情况

1.1.2 代码实现

1.1.2.1 情况一代码

1.1.2.2 情况二代码

1.2 缺失值填补

fillna()

1.2.1 使用常数填补缺失值

1.2.2 使用上一个或下一个非缺失值填补

1.2.3 使用平均值填补缺失值

1.2.4 使用众数填补缺失值

1.2.5 使用中位数填补缺失值

1.2.6 使用缺失值前一个与后一个非缺失值的均值填补

1.2.7 使用拉格朗日插值法对缺失值进行填补

1.2.7.1 拉格朗日插值法

1.2.7.2 代码

1.2.8 使用预测模型对缺失值进行填补

2. 异常值处理

2.1 异常值的检测

2.1.1 3σ 准则(拉依达准则)

相关概念

数据分布图绘制

2.1.2 箱线图检测

相关概念

箱线图绘制

2.2 异常值的处理

2.2.1 对不在指定取值范围内的异常值处理

删除异常值

异常值置为空值

2.2.2 基于 3σ 准则(拉依达准则)的异常值处理

2.2.3 基于箱线图检测的异常值处理

3. 重复值处理

返回文章目录

数据、文献

数据、文献：
「[Python] 数据预处理(缺失…异常值、重复值)」

返回文章目录

1. 缺失值处理

对于缺失值一般有两种处理方式：
- 1.将缺失值直接删除
- 2.对缺失值进行填补

返回文章目录

1.1 缺失值删除

返回文章目录

1.1.1 适用情况

对于缺失值采用直接删除的方式进行处理有如下几种情况：
- 1.对于数据表中的一行，如果整行数据缺失，或者是在一行中所需要使用的数据列对应的数据缺失，那么可以将这一行直接进行删除。
  如：
- 2.如果在一行或者一列中存在大量的数据缺失，那么可以对该行或该列直接进行删除。
  
  在一行或一列中，数据的缺失量是否达到需要删除该行或该列，需要视情况而定，这没有十分准确的标准。
  
  如：
  
  表1：
  表2：

返回文章目录

1.1.2 代码实现

返回文章目录

1.1.2.1 情况一代码

通过调用 dropna() 方法，删除整行数据缺失的行，或者在一行中所需要使用的数据列对应的数据缺失的行。

dropna()：
参数：
- axis：表示轴向，0为删除行，1为删除列，默认为0.
- how：接收 string 类型的数据为参数，表示删除的方式，any 表示只要有缺失值就删除该行或列，all表示全部为缺失值才删除行或列。默认为any。
- subset：接收 array 类型的数据为参数，表示进行缺失值处理的行或列，默认为None，表示所有的行或列。
- inplace：表示是否在原表上进行操作，默认为False。

# 包的导入
import pandas as pd
# 读取数据
data = pd.read_excel('../../监测点C逐日污染物浓度实测数据.xlsx')
# 删除数据缺失的行
# 当 subset 指定的列全部缺失才删除对应的行
data_new = data.dropna(
  how='all', 
  subset=[
    'SO2实测日均(μg/m³)', 
    'NO2实测日均(μg/m³)', 
    'PM10实测日均(μg/m³)', 
    'PM2.5实测日均(μg/m³)', 
    'O3实测八小时滑动平均日最大值(μg/m³)', 
    'CO实测日均(mg/m³)'
  ]  
)
# print(data_new)
# 导出处理后的数据
data_new.to_excel('./1.xlsx')

返回文章目录

1.1.2.2 情况二代码

如果在一行中存在大量的数据缺失，直接删除该行。

数据表表1

中一共有8列数据，除去第一第二列，剩下六列数据，当一行中缺失的数据大于等于4个时，将该行删除。

先调用 apply() 方法对数据表的每行进行处理，然后再对数据表中需要删除的行进行删除。

apply()：
参数：
- func：接收一个函数作为参数，该函数为对数据表中的每行或每列进行处理的函数，该函数接收有一个参数，用于接收传入的数据表中的行或列。
- axis：轴向，axis=1表示对数据表中的每行进行处理，axis=0表示对数据表中的每列进行处理。

# 包的导入
import pandas as pd
import numpy as np
# 读取数据
data = pd.read_excel('../../监测点C逐日污染物浓度实测数据.xlsx')

# 当一行中的数据，除去第一第二列，
# 缺失的数据个数大于等于4(该表中一共8列数据)
# 返回空行
# 否则将原来的行返回
def fun(row):
  sub_row = row[2:]
  cnt = sub_row.count()
  if cnt<=2 :
    # return None
    return np.nan
  else :
    return row

# 调用 apply() 方法对每行数据进行处理
re = data.apply(fun, axis=1)
# 删除整行数据为空的行，直接修改原表
re.dropna(how='all', inplace=True)

如果在一列中存在大量的数据缺失，直接删除该列。

通过对表2

中，每列非空数据的统计，发现湿度这一列存在大量的数据缺失，所以将这列数据整列进行删除。
- 删除指定列的方法：
  - pop()：
  - pop() 方法一次只能删除一列数据，且是对原数组直接进行列的删除，同时会返回删除的列的数据。
  - 参数：
    - item：需要删除的列的列名。
  - drop()：
  - drop() 方法支持多列删除，不对原数组直接进行列的删除，会返回一个删除指定列后的新数组。
  - 参数：
    - labels：接收一个字符串类型数据或一个序列为参数，表示要删除的列。
    - axis：轴向，axis=1表示对列进行删除，axis=0表示对行进行删除。
(1)使用 pop() 方法删除指定列：
```
# 包的导入
import pandas as pd
# 读取数据
data = pd.read_excel('../../监测点C逐小时污染物浓度与气象实测数据.xlsx')
# 删除指定列
data.pop('湿度(%)')
data
```
(2)使用 drop() 方法删除指定列：
```
# 包的导入
import pandas as pd
# 读取数据
data = pd.read_excel('../../监测点C逐小时污染物浓度与气象实测数据.xlsx')
# 删除指定列
re = data.drop('湿度(%)', axis=1)
re
```
```
# 包的导入
import pandas as pd
# 读取数据
data = pd.read_excel('../../监测点C逐小时污染物浓度与气象实测数据.xlsx')
# 删除指定列
re = data.drop(['湿度(%)'], axis=1)
re
```
(3)使用 apply() 方法对每列进行处理，然后使用 dropna() 方法删除数据量缺失过大的列：
- apply()：
- 参数：
  - func：接收一个函数作为参数，该函数为对数据表中的每行或每列进行处理的函数，该函数接收有一个参数，用于接收传入的数据表中的行或列。
  - axis：轴向，axis=1表示对数据表中的每行进行处理，axis=0表示对数据表中的每列进行处理。
- dropna()：
- 参数：
  - axis：表示轴向，0为删除行，1为删除列，默认为0.
  - how：接收 string 类型的数据为参数，表示删除的方式，any 表示只要有缺失值就删除该行或列，all表示全部为缺失值才删除行或列。默认为any。
  - subset：接收 array 类型的数据为参数，表示进行缺失值处理的行或列，默认为None，表示所有的行或列。
  - inplace：表示是否在原表上进行操作，默认为False。
假设数据的缺失达到0.3为数据缺失过多，需要将该列进行删除。
湿度这列非空的数据个数为13310，表2中的总行数为19491，湿度列的数据缺失已达0.3，所有要将湿度这一列进行删除。
```
# 包的导入
import pandas as pd
import numpy as np
# 读取数据
data = pd.read_excel('../../监测点C逐小时污染物浓度与气象实测数据.xlsx')
# 获取所有列中非空数据个数最多的列的数据个数
max_num = data.count().max()

# 处理数据表中的每列
# 数据缺失过多，将整列修改为空
def fun(col):
  # print(col.count())
  # 计算每列的非空数据个数
  num = col.count()
  # 假设数据缺失达到0.3为数据缺失过多
  # 需要对该列进行删除
  if (num/max_num < 0.7):
    # 返回空
    return np.nan
  else:
    return col  

# re = data.apply(fun)
re = data.apply(fun, axis=0)
# 删除整列为空的列
re.dropna(how='all', inplace=True, axis=1)
```

返回文章目录

1.2 缺失值填补

对缺失值进行填补，有如下几种方法：
- 1.使用一个常数对表中的所有缺失值进行填补。
- 2.使用缺失值所在的行或列的上一个或下一个非缺失值进行填补。
- 3.使用缺失值所在的行或列的平均值进行填补。
- 4.使用缺失值所在的行或列的众数进行填补。
- 5.使用缺失值所在的行或列的中位数进行填补。
- 6.使用缺失值所在的行或列的前一个和后一个非缺失值的均值进行填补。
- 7.使用拉格朗日插值法对缺失值进行填补
- 8.使用预测模型对缺失值进行填补

使用哪种缺失值填补方法对缺失值进行填补，需要根据数据所在的实际场景进行分析与选择，使得缺失值填补后，对最后的结果造成的影响尽可能的小。

一般缺失值的填补是针对存在少量数据缺失的行或列，或者是删除整行数据缺失的行和大量数据缺失的行与列后数据集中仍有部分数据缺失的行或列。
如：

返回文章目录

fillna()

参数：
- value：表示用来替换缺失值的值
- method：接收 string 为参数，backfill或bfill表示使用下一个非缺失值进行替换，pad或ffill表示使用上一个非缺失值进行替换，默认为None
- axis：表示轴向，axis=1表示在一行中如果有缺失值，使用上一列或下一列的数据来填补缺失值；axis=0表示在一列中如果有缺失值，使用上一行或下一行的数据来填补缺失值。
- inplace：表示是否在原表上进行操作，默认为False。
- limit：表示填补缺失值的个数上限，默认为None
value与method选择其一即可

以下的举例均不考虑实际的应用情况和实际场景。
每个例子使用的都为原始的表格，没有经过预处理。

返回文章目录

1.2.1 使用常数填补缺失值

调用 fillna() 方法，使用一个常数对数据表中所有的缺失值进行填补。

# 包的导入
import pandas as pd
import numpy as np
# 读取数据
data = pd.read_excel('../../监测点C逐小时污染物浓度与气象实测数据.xlsx')
# 使用 999 填补数据表中的所有缺失值
re = data.fillna(value=999)
re

返回文章目录

1.2.2 使用上一个或下一个非缺失值填补

调用 fillna() 方法，使用缺失值的上一个或下一个非缺失值对数据表中所有的缺失值进行填补。

由于湿度这一列第一行的数据为空，所以使用缺失值的下一行非缺失值对缺失的数据进行填补。

# 包的导入
import pandas as pd
import numpy as np
# 读取数据
data = pd.read_excel('../../监测点C逐小时污染物浓度与气象实测数据.xlsx')
# 使用缺失值的下一行非缺失值填补数据表中的所有缺失值
re = data.fillna(method='bfill', axis=0)
re

返回文章目录

1.2.3 使用平均值填补缺失值

调用 fillna() 方法，使用每列的平均值对数据表中对应列的缺失值进行填补。

mean()：
- 获取调用该方法的数据集的一行或一列的平均值。
- axis：轴向，默认 axis=0 计算每列的算数平均数，axis=1 计算每行的算数平均数。

经过验证，调用 mean() 方法计算列的均值，空值(缺失值)不会计算在内。

# 包的导入
import pandas as pd
import numpy as np

# 读取数据
data = pd.read_excel('../../监测点C逐小时污染物浓度与气象实测数据.xlsx')

# 由于表格中的部分缺失值使用字符串类型的'—' 'NULL' 'NA' 表示
# 所有先对这些数据进行处理
def fun(x):
  if (x=='—' or x=='NULL' or x=='NA'): return np.nan
  else: return x
# applymap() 方法会遍历并处理表格中每个单元格的数据
# fun 为传入的函数参数，用于处理每个单元格
# fun 函数会接收一个参数，为表格中每个单元格的数据
data = data.applymap(fun)

# 使用每列的均值对每列中的缺失值进行填补
# def fun_mean(col):
#   如果当前列是第二列直接退出函数
#   第二列的数据为字符串类型
#   if (col.name == '地点'): return col
#   col.fillna(value=col.mean(), inplace=True)
#   return col

# re = data.apply(fun_mean)

# 循环处理第三列及往后的每列
# 使用每列的均值对每列中的缺失值进行填补
for col_name in data.columns[2:]:
  # 当前要处理的列
  col = data[col_name]
  # 使用当前列的均值填补缺失值
  col.fillna(value=col.mean(), inplace=True)
  # 更新原数据表
  data[col_name] = col

data

返回文章目录

1.2.4 使用众数填补缺失值

调用 fillna() 方法，使用每列的众数对数据表中对应列的缺失值进行填补。

mode()：
- 获取调用该方法的数据集的一行或一列的众数。如果个数最多的取值存在多个，则返回多个值。
- axis：轴向，默认 axis=0 获取每列的众数，axis=1 获取每行的众数。

湿度这一列的取值情况如下：

# 包的导入
import pandas as pd
import numpy as np

# 读取数据
data = pd.read_excel('../../监测点C逐小时污染物浓度与气象实测数据.xlsx')

# 由于表格中的部分缺失值使用字符串类型的'—' 'NULL' 'NA' 表示
# 所有先对这些数据进行处理
def fun(x):
  if (x=='—' or x=='NULL' or x=='NA'): return np.nan
  else: return x
# applymap() 方法会遍历并处理表格中每个单元格的数据
# fun 为传入的函数参数，用于处理每个单元格
# fun 函数会接收一个参数，为表格中每个单元格的数据
data = data.applymap(fun)

# 使用每列的众数对每列中的缺失值进行填补
def fun_(col):
  # 获取第一个众数填补缺失值
  col.fillna(value=col.mode()[0], inplace=True)
  return col

re = data.apply(fun_)
re

返回文章目录

1.2.5 使用中位数填补缺失值

调用 fillna() 方法，使用每列的中位数对数据表中对应列的缺失值进行填补。

median()：
- 获取调用该方法的数据集的一行或一列的中位数。
- axis：轴向，默认 axis=0 获取每列的中位数，axis=1 获取每行的中位数。

湿度这一列的中位数如下：

# 包的导入
import pandas as pd
import numpy as np

# 读取数据
data = pd.read_excel('../../监测点C逐小时污染物浓度与气象实测数据.xlsx')

# 由于表格中的部分缺失值使用字符串类型的'—' 'NULL' 'NA' 表示
# 所有先对这些数据进行处理
def fun(x):
  if (x=='—' or x=='NULL' or x=='NA'): return np.nan
  else: return x
# applymap() 方法会遍历并处理表格中每个单元格的数据
# fun 为传入的函数参数，用于处理每个单元格
# fun 函数会接收一个参数，为表格中每个单元格的数据
data = data.applymap(fun)

# 使用每列的中位数对每列中的缺失值进行填补
def fun_(col):
  # 如果当前列是第二列直接退出函数
  # 第二列的数据为字符串类型
  if (col.name == '地点'): return col
  col.fillna(value=col.median(), inplace=True)
  return col

re = data.apply(fun_)
re

返回文章目录

1.2.6 使用缺失值前一个与后一个非缺失值的均值填补

调用 interpolate() 方法，使用每列的缺失值前一个与后一个非缺失值的均值对数据表中对应列的缺失值进行填补。

如果第一行就存在缺失值，则本方法不适用，缺失值不会被填补，仍然为 NaN。

当前的测试数据如下：

# 包的导入
import pandas as pd
import numpy as np

# 读取数据
data = pd.read_excel('../../1.xlsx')

# 由于表格中的部分缺失值使用字符串类型的'—' 'NULL' 'NA' 表示
# 所有先对这些数据进行处理
def fun(x):
  if (x=='—' or x=='NULL' or x=='NA'): return np.nan
  else: return x
# applymap() 方法会遍历并处理表格中每个单元格的数据
# fun 为传入的函数参数，用于处理每个单元格
# fun 函数会接收一个参数，为表格中每个单元格的数据
data = data.applymap(fun)

# 使用每列的缺失值前一个与后一个非缺失值的均值
# 对每列中的缺失值进行填补
def fun_(col):
  # 第一列为时间类型直接退出函数
  if (col.name == '实测日期'): return col
  # 如果当前列是第二列直接退出函数
  # 第二列的数据为字符串类型
  if (col.name == '地点'): return col
  # col = col.interpolate()
  # 直接修改原数据
  col.interpolate(inplace=True)
  return col

re = data.apply(fun_)
re

返回文章目录

1.2.7 使用拉格朗日插值法对缺失值进行填补

以下内容来自：
[1]赵莉,孙娜,李丽萍,崔杰.拉格朗日插值法在数据清洗中的应用[J].辽宁工业大学学报(自然科学版),2022,42(02):102-105+117.DOI:10.15916/j.issn1674-3261.2022.02.007.
文献知网连接

返回文章目录

1.2.7.1 拉格朗日插值法

拉格朗日多项式插值法的基本思想是：给出一个恰好穿过二维平面上几个已知点的多项式，利用最小次数的多项式来构建一条光滑曲线，使曲线通
过所有已知点。

对于平面中的n个已知点(一条直线上无两点)，可以找到一个n-1次多项式：

$y=a_{0}+a_{1} x^{2}+a_{2} x+\cdots+a_{n-1} x^{n-1}$

使得此多项式对应的曲线通过这n个点。将n个点的坐标 ( $x_1$ , $y_1$ ), ( $x_2$ , $y_2$ ), …, ( $x_n$ , $y_n$ )代入多项式中得到：

$\begin{array}{c} y_{1}=a_{0}+a_{1} x_{1}+a_{2} x_{1}^{2}+a_{n-1} x_{1}^{n-1} \\ y_{2}=a_{0}+a_{1} x_{2}+a_{2} x_{2}^{2}+a_{n-1} x_{2}^{n-1} \\ \ldots \\ y_{n}=a_{0}+a_{1} x_{n}+a_{2} x_{n}^{2}+a_{n-1} x_{n}^{n-1} \end{array}$

解得拉格朗日插值多项式如下：

$L(x)=\sum_{i=0}^{n} y_{i} \prod_{j=0, j \neq i}^{n} \frac{x-x_{j}}{x_{i}-x_{j}}$

例如，平面上有 4 个点，(4, 10)、（5, 5.25）、(6, 1)、(18, ?)，根据拉格朗日插值法计算缺失“?”的值：

$\begin{aligned} L(x)=& 10 \frac{(x-5)(x-6)}{(4-5)(4-6)}+5.25 \frac{(x-4)(x-6)}{(5-4)(5-6)}+\\ & \frac{(x-4)(x-5)}{(6-4)(6-5)}=\frac{1}{4}\left(x^{2}-28 x+136\right) \end{aligned}$

将 x=18 代入可以得到 L(18)=-11，因此缺失的值是-11。

返回文章目录

1.2.7.2 代码

当前将要进行缺失值填补的数据：

为了防止取缺失值前后的非缺失值时索引越界，对文献中的代码进行了修改

import numpy as np
import pandas as pd
# 引入拉格朗日插值法所需的方法
from scipy.interpolate import lagrange

# 文件读取
data = pd.read_excel('../../1.xlsx')

# 字符串表示的空值预处理
def fun(x):
  if (x=='—' or x=='NULL' or x=='NA'): return np.nan
  else: return x

data = data.applymap(fun)

# 生成拉格朗日插值
def interpolate_columns(data_col, missing_val_idx, k=5):
  """
  data_col: 需要进行缺失值填补的列
  missing_val_idx: 数据缺失的单元格在该列对应的索引
  k: 缺失值前后取值的个数, 默认为5个

  return: 返回拉格朗日插值
  """
  # 防止取缺失值前后的非缺失值时下标越界
  # 向缺失值前取值的个数，默认为 k
  f_k = k
  # 如果缺失值前还有的数值个数小于 k
  # 更改取值个数
  if(missing_val_idx < k): f_k = missing_val_idx
  # 向缺失值后取值的个数，默认为 k
  b_k = k
  # 如果缺失值后还有的数值个数小于 k
  # 更改取值个数
  if((data_col.size-missing_val_idx-1) < k): b_k = data_col.size-missing_val_idx-1
  # 获取二者的较小值
  if(f_k <= b_k): k = f_k
  else: k = b_k
  # 取出当前缺失值位置前后 k 个值
  y = data_col[ 
    list(range(missing_val_idx-k, missing_val_idx))  + list(range(missing_val_idx+1, missing_val_idx+1+k)) 
  ]
  # 去除空值
  y = y[ y.notnull() ]
  # 生成拉格朗日插值函数
  f = lagrange(y.index, list(y))
  # 计算并返回缺失值将要填补的数据值
  return f(missing_val_idx)

# 遍历数据表
# 每列
for i in data.columns[2:]:
  # 遍历每列中的每个单元格
  for j in range(data[i].size):
    # 如果单元格为空
    # 进行拉格朗日插值
    if data[i].isnull()[j]:
      data[i][j] = interpolate_columns(data[i], j)

data

此代码无法对数据表第一行与最后一行存在的缺失值进行填补，由于代码修改，当缺失值在第一行或最后一行时，取缺失值前后的非缺失值的个数为0，所以无法使用拉格朗日插值法进行数据的填补。

文献中的代码：

返回文章目录

1.2.8 使用预测模型对缺失值进行填补

预测模型较多，后面补上

返回文章目录

2. 异常值处理

返回文章目录

2.1 异常值的检测

检查数据集中的异常值，常用的方法有：
- 3σ 准则(拉依达准则)
- 箱线图检测

返回文章目录

2.1.1 3σ 准则(拉依达准则)

符号	说明
$\mu$	数学期望(均值)
${\sigma}^{2}$	方差
$\sigma$	标准差

数据分布图绘制

seaborn.distplot()：
参数：
- a：接收一维数组或列表为参数，为绘制图形的数据。
- hist：是否显示直方图，默认值为 True，默认情况下显示直方图。
- kde：是否显示核密度估计，默认值为 True，默认情况下显示核密度估计。
- bins：接收 int 或 list 类型的数据为参数，控制直方图的划分，即直方图有几柱。
- rug：是否绘制变量的分布情况，默认值为 False，默认情况下不显示。
- fit：
- hist_kws：接收字典类型的数据为参数，设置绘制的直方图的显示样式。
- kde_kws：接收字典类型的数据为参数，设置绘制的核密度估计的显示样式。
- rug_kws：接收字典类型的数据为参数，设置绘制的变量分布情况的显示样式。
- color：设置绘制图形的颜色。
- vertical：绘制的图形x轴与y轴是否进行对调，绘制的图形显示在x轴还是y轴，默认值为False，显示在x轴。
- norm_hist：控制直方图的高度(y轴)显示的是密度还是计数。在不含有核密度估计的图形中，默认为 False，显示的为计数。在含有核密度估计的图形中，默认为 True，显示的为密度。
- axlabel：接收字符串类型的数据为参数，用于设置x轴的标签。
- label：接收字符串类型的数据为参数，用于设置直方图的图例。
- ax：seaborn.distplot() 会返回一个坐标轴对象，可以用于设置图形的四个坐标轴。

参考：
【Python可视化 | Seaborn之seaborn.distplot()】鹿港小小镇
【sns.distplot()用法】小小喽啰

数据文件名：
监测点A逐小时污染物浓度与气象实测数据_去除整行缺失_补全数据_去除负数.xlsx

这里只进行简单的测试，更加详细的测试【待写】

绘制 SO2监测浓度的数据分布图

import pandas as pd
# 画图所需的包
import matplotlib.pyplot as plt
# 绘制数据分布图所需的包
import seaborn as sns

# 提高 matplotlib 在 jupyter 中作图的分辨率
%config InlineBackend.figure_format = 'retina'
# 处理中文与负号的显示问题
plt.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题

# 读取数据
data = pd.read_excel('./监测点A逐小时污染物浓度与气象实测数据_去除整行缺失_补全数据_去除负数.xlsx')

# 修改列名
data.columns = ['监测时间', '地点', 'SO2监测浓度', 'NO2监测浓度', 'PM10监测浓度',
       'PM2.5监测浓度', 'O3监测浓度', 'CO监测浓度', '温度', '湿度',
       '气压', '风速', '风向']

# 绘制数据分布图
# ax 接收返回的坐标轴对象
ax = sns.distplot(
  # 绘制图形的数据
  data['SO2监测浓度'],
  # 直方图柱 20个 
  bins=20, 
  # 显示变量的分布情况
  rug=True,
  # 直方图样式设置
  hist_kws={
    'label': 'SO2监测浓度',
    'color': 'red'
  },
  # 核密度估计曲线样式设置
  kde_kws={
    'label': 'SO2监测浓度核密度估计',
    'color': 'green'
  },
  # 设置x轴的标签
  axlabel= r'$SO_{2}$'
)
# 取消上轴和右轴的显示
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
# 显示图例
plt.legend()
plt.show()

返回文章目录

2.1.2 箱线图检测

以下内容来自：
[1]孙向东,刘拥军,陈雯雯,贾智宁,黄保续.箱线图法在动物卫生数据异常值检验中的运用[J].中国动物检疫,2010,27(07):66-68.
知网文献链接

箱线图绘制

以下博客对于绘制箱线图的方法参数介绍的很详细，这里不在进行介绍。

matplotlib.pyplot.boxplot()

两篇文章中都有详细的方法参数说明
【python绘制箱线图boxplot()】小朱小朱绝不服输
【Python 箱型图的绘制并提取特征值】流浪猪头拯救地球

将方法的参数及其说明复制在这：
x：指定要绘制箱线图的数据，可以是一组数据也可以是多组数据；
notch：是否以凹口的形式展现箱线图，默认非凹口；
sym：指定异常点的形状，默认为蓝色的+号显示；
vert：是否需要将箱线图垂直摆放，默认垂直摆放；
whis：指定上下须与上下四分位的距离，默认为1.5倍的四分位差；
positions：指定箱线图的位置，默认为range(1, N+1)，N为箱线图的数量；
widths：指定箱线图的宽度，默认为0.5；
patch_artist：是否填充箱体的颜色，默认为False；
meanline：是否用线的形式表示均值，默认用点来表示；
showmeans：是否显示均值，默认不显示；
showcaps：是否显示箱线图顶端和末端的两条线，默认显示；
showbox：是否显示箱线图的箱体，默认显示；
showfliers：是否显示异常值，默认显示；
boxprops：设置箱体的属性，如边框色，填充色等；
labels：为箱线图添加标签，类似于图例的作用；即箱线图对应x轴点的名字
flierprops：设置异常值的属性，如异常点的形状、大小、填充色等；
medianprops：设置中位数的属性，如线的类型、粗细等；
meanprops：设置均值的属性，如点的大小、颜色等；
capprops：设置箱线图顶端和末端线条的属性，如颜色、粗细等；
whiskerprops：设置须的属性，如颜色、粗细、线的类型等；
manage_ticks：是否自适应标签位置，默认为True；
autorange：是否自动调整范围，默认为False；

seaborn.boxplot()

第一篇文章有详细的方法参数说明及代码示例，第二篇文章主要是代码示例
【超详细Seaborn绘图 ——（二）boxplot & boxenplot】邱之涵0
【Python画箱型图之seaborn】随风而逝*

将方法的参数及其说明复制在这：
x, y, hue：数据或向量数据中的变量名称
用于绘制长格式数据的输入。

data：DataFrame，数组，数组列表
用于绘图的数据集。
如果x和y都缺失，那么数据将被视为宽格式。
否则数据被视为长格式。

order, hue_order：字符串列表
控制分类变量（对应的条形图）的绘制顺序，
若缺失则从数据中推断分类变量的顺序。

orient：“v”或“h”
控制绘图的方向（垂直或水平）。
这通常是从输入变量的 dtype 推断出来的，
但是当“分类”变量为数值型或绘制宽格式数据时
可用于指定绘图的方向。

color：matplotlib颜色
所有元素的颜色，或渐变调色板的种子颜色。

palette：调色板名称，列表或字典
用于hue变量的不同级别的颜色。
可以从color_palette()得到一些解释，
或者将色调级别映射到matplotlib颜色的字典。

saturation：float
控制用于绘制颜色的原始饱和度的比例。
通常大幅填充在轻微不饱和的颜色下看起来更好，
如果您希望绘图颜色与输入颜色规格完美匹配
可将其设置为1。

width：float
不使用色调嵌套时完整元素的宽度，
或主要分组变量一个级别的所有元素的宽度。

dodge：bool
使用色调嵌套时，元素是否应沿分类轴移动。

fliersize：float
用于表示异常值观察的标记的大小。

linewidth：float
构图元素的灰线宽度。

whis：float
控制在超过高低四分位数时 IQR （四分位间距）的比例，
因此需要延长绘制的触须线段。超出此范围的点将被识别为异常值。

notch：boolean
是否使矩形框“凹陷”以指示中位数的置信区间。
还可以通过plt.boxplot的一些参数来控制

ax：matplotlib轴
绘图时使用的 Axes 轴对象，否则使用当前 Axes 轴对象

kwargs：键值映射
其他在绘图时传给plt.boxplot的参数
设置方法与 plt.boxplot 一样

数据文件名：
监测点A逐小时污染物浓度与气象实测数据_去除整行缺失_补全数据_去除负数.xlsx

绘制 SO2监测浓度的箱线图
测试一些经常会使用的参数和参数的常用设置

matplotlib.pyplot.boxplot()

import pandas as pd
# 画图所需的包
import matplotlib.pyplot as plt

# 提高 matplotlib 在 jupyter 中作图的分辨率
%config InlineBackend.figure_format = 'retina'
# 处理中文与负号的显示问题
plt.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题

# 读取数据
data = pd.read_excel('./监测点A逐小时污染物浓度与气象实测数据_去除整行缺失_补全数据_去除负数.xlsx')

# 修改列名
data.columns = ['监测时间', '地点', 'SO2监测浓度', 'NO2监测浓度', 'PM10监测浓度',
       'PM2.5监测浓度', 'O3监测浓度', 'CO监测浓度', '温度', '湿度',
       '气压', '风速', '风向']

# 绘制箱线图
plt.boxplot(
  # 绘图数据
  data['SO2监测浓度'],
  # 箱子是否内凹
  # notch=True,
  # 设置异常点的形状
  # sym='.',
  # 填充箱体颜色
  patch_artist=True,
  # 显示平均值，默认使用点显示
  showmeans=True,
  # 设置箱子的宽度
  widths=0.1,
  # 设置箱子的样式，需要 patch_artist=True
  boxprops={
    # 箱子的边框为灰色
    'color': 'gray',
    # 箱子的填充色为橙色
    'facecolor': 'orange',
    # 设置边框线的宽度
    'linewidth': '2'
  },
  # 设置异常值点的样式
  flierprops={
    # 设置点的形状
    'marker': '.',
    # 设置点的填充色
    'markerfacecolor': 'blue',
    # 设置点的边框色
    'markeredgecolor': 'blue',
    # 设置点的大小
    'markersize': '2'
  },
  # 添加箱线图在x轴对应位置的名字
  # x轴坐标点名
  labels=['SO2监测浓度'],
  # 设置须的样式
  whiskerprops={
    # 设置线的颜色
    'color': 'green'
  },
  # 设置箱线图最值线的样式
  capprops={
    # 设置线的颜色
    'color': 'red',
    # 设置线的宽度
    'linewidth': '3'
  }
)
plt.grid(linestyle=':')
# 显示图例
plt.legend()
plt.show()

绘制所有列的箱线图
测试一些经常会使用的参数和参数的常用设置

seaborn.boxplot()

import pandas as pd
# 画图所需的包
import matplotlib.pyplot as plt
# 绘制数据分布图所需的包
import seaborn as sns

# 提高 matplotlib 在 jupyter 中作图的分辨率
%config InlineBackend.figure_format = 'retina'
# 处理中文与负号的显示问题
plt.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题

# 读取数据
data = pd.read_excel('./监测点A逐小时污染物浓度与气象实测数据_去除整行缺失_补全数据_去除负数.xlsx')

# 修改列名
data.columns = ['监测时间', '地点', 'SO2监测浓度', 'NO2监测浓度', 'PM10监测浓度',
       'PM2.5监测浓度', 'O3监测浓度', 'CO监测浓度', '温度', '湿度',
       '气压', '风速', '风向']
       
# 设置画布大小
plt.figure(figsize=(18, 5))

# 绘制箱线图
# 会返回一个坐标轴对象
ax = sns.boxplot(
  # x = data['NO2监测浓度'],
  # 绘图的数据
  # y = data['SO2监测浓度'],
  # 传入 DataFrame 类型的数据，会绘制每列的箱线图
  data=data,
  # 箱子的填充色
  # 有多个箱子，多个箱子的颜色都会一致
  # color='red',
  # 设置调色板，会根据调色板的颜色映射规则对箱子填充颜色
  palette='viridis',
  # 设置箱子的宽度
  width=0.7,
  # 异常值点的大小
  fliersize=2,
  # 箱线图中边框、线的宽度
  linewidth=1.2,
  # 箱子内凹
  notch=True,
  # 其他样式设置, 与 matplotlib.pyplot.boxplot() 一样
  # 显示均值
  showmeans=True,
  # 设置异常值点的样式
  flierprops={
    # 设置点的形状
    'marker': '.',
    # 设置点的填充色
    'markerfacecolor': 'blue',
    # 设置点的边框色
    'markeredgecolor': 'blue',
    # 设置点的大小
    'markersize': '2'
  }
)

# 取消上轴和右轴的显示
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_color('none')

plt.grid(linestyle=':')
# 显示图例
plt.legend()
plt.show()

返回文章目录

2.2 异常值的处理

需要进行异常值处理的情况，主要有如下几种：
- 1.数值的取值范围有明确的要求，对于不在要求的取值范围内的数据可以进行异常值的处理。如，要求取值要为正数，对于取值为负数的数值需要进行处理。
- 2.使用 3σ 准则(拉依达准则)检测异常值，对于落在（μ-3σ,μ+3σ）以外的数据需要进行异常值处理。
- 3.使用箱线图检测异常值，对于落在异常值截断线以外的数据需要进行异常值处理。
异常值处理的方式：
- 1.直接将异常值删除。
- 2.将异常值置为空，采用缺失值填补的方法对异常值进行替换。

返回文章目录

2.2.1 对不在指定取值范围内的异常值处理

数据文件名：
监测点A逐小时污染物浓度与气象实测数据_去除整行缺失_数据填补.xlsx

data['SO2监测浓度(μg/m³)'].value_counts()

统计 SO2监测浓度(μg/m³) 的取值情况：
存在16个数据取值为负数，由于浓度大于等于0，所以对取值为负数的异常值进行处理。

未处理前的数据情况：

返回文章目录

删除异常值

由于 SO2监测浓度(μg/m³) 取值为负数的数据个数并不多，所以将 SO2监测浓度(μg/m³) 取值为负数的行直接删除。

# 包的引入
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# 读取数据
data = pd.read_excel('../22/监测点A逐小时污染物浓度与气象实测数据_去除整行缺失_数据填补.xlsx')

# 删除 SO2监测浓度(μg/m³) 取值为负数的行
# 即取出 SO2监测浓度(μg/m³) 取值大于等于0的行
re = data[data['SO2监测浓度(μg/m³)']>=0]
re.count()

返回文章目录

异常值置为空值

未处理前的数据情况：

# 包的引入
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# 读取数据
data = pd.read_excel('../22/监测点A逐小时污染物浓度与气象实测数据_去除整行缺失_数据填补.xlsx')

# 深复制一份数据
data1 = data.copy() 
# 将 SO2监测浓度(μg/m³) 列中取值为负数的数据置为空值
data1['SO2监测浓度(μg/m³)'][data1['SO2监测浓度(μg/m³)']<0] = pd.NA
data1.count()

返回文章目录

2.2.2 基于 3σ 准则(拉依达准则)的异常值处理

这里只进行异常值的筛选，不进行处理，若要处理可以采用与 2.2.1 中类似的方法进行处理，删除异常值或者置为空值后填补异常值。

# 包的引入
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# 提高 matplotlib 在 jupyter 中作图的分辨率
%config InlineBackend.figure_format = 'retina'
# 处理中文与负号的显示问题
plt.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题

# 读取数据
data = pd.read_excel('../22/监测点A逐小时污染物浓度与气象实测数据_去除整行缺失_数据填补.xlsx')

# 获取 SO2监测浓度(μg/m³) 列
so2 = data['SO2监测浓度(μg/m³)']
# 计算均值与标准差
mean_so2 = so2.mean()
std_so2 = so2.std()
print(mean_so2, std_so2)

# 计算 μ-3σ μ+3σ
left = mean_so2 - 3*std_so2
right = mean_so2 + 3*std_so2

# 绘制数据分布图
# ax 接收返回的坐标轴对象
ax = sns.distplot(
  # 绘制图形的数据
  data['SO2监测浓度(μg/m³)'],
  # 显示变量的分布情况
  rug=True,
  # 设置x轴的标签
  axlabel= r'$SO_{2}$'
)

# 绘制 μ-3σ μ+3σ
plt.axvline(left, linestyle='--', color='orange')
plt.axvline(right, linestyle='--', color='orange')

# 显示图例
plt.legend()
plt.show()

# 复制数据集
data1 = data.copy()
# 筛选出 SO2监测浓度(μg/m³) 列取值不在 (μ-3σ, μ+3σ) 内的行
data1 = data1[np.abs(data1['SO2监测浓度(μg/m³)']-mean_so2) > 3*std_so2]
data1

均值与标准差


基于 3σ 准则(拉依达准则) 筛选出的 SO2监测浓度(μg/m³) 取值异常的行：

返回文章目录

2.2.3 基于箱线图检测的异常值处理

这里只进行异常值的筛选，不进行处理，若要处理可以采用与 2.2.1 中类似的方法进行处理，删除异常值或者置为空值后填补异常值。

# 包的引入
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns


# 提高 matplotlib 在 jupyter 中作图的分辨率
%config InlineBackend.figure_format = 'retina'
# 处理中文与负号的显示问题
plt.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题

# 读取数据
data = pd.read_excel('../22/监测点A逐小时污染物浓度与气象实测数据_去除整行缺失_数据填补.xlsx')

# 获取 SO2监测浓度(μg/m³) 列
so2 = data['SO2监测浓度(μg/m³)']

# 绘制箱线图
plt.boxplot(
  # 绘图数据
  so2,
  # 填充箱体颜色
  patch_artist=True,
  # 显示平均值，默认使用点显示
  showmeans=True,
  # 设置箱子的宽度
  widths=0.1,
  # 设置箱子的样式，需要 patch_artist=True
  boxprops={
    # 箱子的边框为黑色
    'color': 'k',
    # 箱子的填充色为橙色
    'facecolor': 'orange',
  },
  # 设置异常值点的样式
  flierprops={
    # 设置点的形状
    'marker': '.',
    # 设置点的填充色
    'markerfacecolor': 'blue',
    # 设置点的边框色
    'markeredgecolor': 'blue',
    # 设置点的大小
    'markersize': '2'
  },
  # 添加箱线图在x轴对应位置的名字
  # x轴坐标点名
  labels=['SO2监测浓度'],
)
plt.grid(linestyle=':')

# 显示图例
plt.legend()
plt.show()

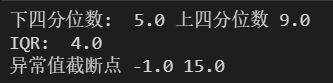
# 获取 SO2监测浓度(μg/m³) 的上下四分位数
bottom, top = so2.quantile([.25, .75])
print('下四分位数: ', bottom, '上四分位数', top)
# 计算 IQR
IQR = top - bottom
print('IQR: ', IQR)
# 计算异常值截断点
top_error = top + 1.5*IQR
bottom_error = bottom - 1.5*IQR
print('异常值截断点', bottom_error, top_error)

# 复制数据集
data1 = data.copy()
data1 = data1[(so2>top_error) | (so2<bottom_error)]
data1

基于箱线图检测筛选出的 SO2监测浓度(μg/m³) 取值异常的行：

返回文章目录

3. 重复值处理

数据集中出现重复值有以下几种情况：
- 1.不同行之间在各列上的取值均相同，即不同行的数据取值完全一致。
- 2.不同行之间存在在某些列上的取值相同

对于重复值可以根据需要，选择对全部列进行去重，也可以选择对某些列进行去重。

可以使用 DataFrame.drop_duplicates() 方法来处理重复值。

DataFrame.drop_duplicates()
参数：
- subset：接收 string 或序列为参数，表示要进行去重的列，默认为None，表示全部的列(只有当一行中所有的列一样，才会对该行进行去重)
- keep：接收 string 为参数，表示重复时保留第几个数据。first：保留第一个。last：保留最后一个。false：只要有重复都不保留。默认为first。
- inplace：表示是否在原表上进行修改。默认为False。

默认情况下，对所有的列进行去重，不在原表上进行修改，有重复值时默认保留重复值的第一个。

代码示例：

l = [
  np.array([1,2,3]),
  np.array([1,1,2]),
  np.array([1,1,2]),
  np.array([1,1,1])
]
df = pd.DataFrame(l)
print(df)
print()
print(df.drop_duplicates())
print()
print(df)

l = [
  np.array([1,2,3]),
  np.array([1,1,2]),
  np.array([1,1,2]),
  np.array([1,1,1])
]
df = pd.DataFrame(l)
print(df)
print()
# 在原表上进行修改，无返回值
# 不在原表上进行修改，会返回修改后的新表
# 对第一第二列的数据进行去重，保留重复值的最后一个
print(df.drop_duplicates(subset=[0,1], inplace=True, keep='last'))
print()
print(df)

返回文章目录

你可能感兴趣的:(Python,python,数据挖掘,数据分析,数据预处理,pandas)

理解Gunicorn：Python WSGI服务器的基石范范0825 ipython linux 运维
理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
Python数据分析与可视化实战指南 William数据分析 python python 数据
在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
python os.environ 江湖偌大 python 深度学习
os.environ['TF_CPP_MIN_LOG_LEVEL']='0'#默认值，输出所有信息os.environ['TF_CPP_MIN_LOG_LEVEL']='1'#屏蔽通知信息（INFO）os.environ['TF_CPP_MIN_LOG_LEVEL']='2'#屏蔽通知信息和警告信息（INFO\WARNING）os.environ['TF_CPP_MIN_LOG_LEVEL']='
Python中os.environ基本介绍及使用方法鹤冲天Pro #Python python 服务器开发语言
文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
Pyecharts数据可视化大屏：打造沉浸式数据分析体验我的运维人生信息可视化数据分析数据挖掘运维开发技术共享
Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
Python教程：一文了解使用Python处理XPath 旦莫 Python进阶 python 开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
python os.environ_python os.environ 读取和设置环境变量 weixin_39605414 python os.environ
>>>importos>>>os.environ.keys()['LC_NUMERIC','GOPATH','GOROOT','GOBIN','LESSOPEN','SSH_CLIENT','LOGNAME','USER','HOME','LC_PAPER','PATH','DISPLAY','LANG','TERM','SHELL','J2REDIR','LC_MONETARY','QT_QPA
使用Faiss进行高效相似度搜索 llzwxh888 faiss python
在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
python是什么意思中文-在python中%是什么意思编程大乐趣
Python中%有两种：1、数值运算：%代表取模，返回除法的余数。如：>>>7%212、%操作符（字符串格式化，stringformatting），说明如下：%[(name)][flags][width].[precision]typecode(name)为命名flags可以有+，-，''或0。+表示右对齐。-表示左对齐。''为一个空格，表示在正数的左侧填充一个空格，从而与负数对齐。0表示使用0填
Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Python python 开发语言大数据数据分析数据挖掘
大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
python八股文面试题分享及解析(1) Shawn________ python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果：21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型，不仅仅改变
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
Python快速入门 —— 第三节：类与对象孤华暗香 Python快速入门 python 开发语言
第三节：类与对象目标：了解面向对象编程的基础概念，并学会如何定义类和创建对象。内容：类与对象：定义类：class关键字。类的构造函数：__init__()。类的属性和方法。对象的创建与使用。示例：classStudent:def__init__(self,name,age,major):self.name&#
pyecharts——绘制柱形图折线图 2224070247 信息可视化 python java 数据可视化
一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd）数据可视化团队研发的ECharts1.0发布到GitHub网站以来，ECharts一直备受业界权威的关注并获得广泛好评，成为目前成熟且流行的数据可视化图表工具，被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言，也加入ECharts的使用行列，并研发出方便Python开发者使用的数据
Python 实现图片裁剪（附代码） | Python工具剑客阿良_ALiang
前言本文提供将图片按照自定义尺寸进行裁剪的工具方法，一如既往的实用主义。环境依赖ffmpeg环境安装，可以参考我的另一篇文章：windowsffmpeg安装部署_阿良的博客-CSDN博客本文主要使用到的不是ffmpeg，而是ffprobe也在上面这篇文章中的zip包中。ffmpy安装：pipinstallffmpy-ihttps://pypi.douban.com/simple代码不废话了，上代码
【华为OD技术面试真题 - 技术面】- python八股文真题题库（4) 算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例：文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片（Slicing）操作**基本切片语法
python os 环境变量 CV矿工 python 开发语言 numpy
环境变量：环境变量是程序和操作系统之间的通信方式。有些字符不宜明文写进代码里，比如数据库密码，个人账户密码，如果写进自己本机的环境变量里，程序用的时候通过os.environ.get（）取出来就行了。os.environ是一个环境变量的字典。环境变量的相关操作importos"""设置/修改环境变量：os.environ[‘环境变量名称’]=‘环境变量值’#其中key和value均为string类
Python爬虫解析工具之xpath使用详解 eqa11 python 爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中，数据提取是一个至关重要的环节。xpath作为一门
【华为OD技术面试真题 - 技术面】- python八股文真题题库（1）算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.数据预处理流程数据预处理的主要步骤工具和库2.介绍线性回归、逻辑回归模型线性回归（LinearRegression）模型形式：关键点：逻辑回归（LogisticRegression）模型形式：关键点：参数估计与评估：3.python浅拷贝及深拷贝浅拷贝（Shal
nosql数据库技术与应用知识点皆过客，揽星河 NoSQL nosql 数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
《Python数据分析实战终极指南》 xjt921122 python 数据分析开发语言
对于分析师来说，大家在学习Python数据分析的路上，多多少少都遇到过很多大坑**，有关于技能和思维的**：Excel已经没办法处理现有的数据量了，应该学Python吗？找了一大堆Python和Pandas的资料来学习，为什么自己动手就懵了？跟着比赛类公开数据分析案例练了很久，为什么当自己面对数据需求还是只会数据处理而没有分析思路？学了对比、细分、聚类分析，也会用PEST、波特五力这类分析法，为啥
Python中深拷贝与浅拷贝的区别 yuxiaoyu.
转自：http://blog.csdn.net/u014745194/article/details/70271868定义：在Python中对象的赋值其实就是对象的引用。当创建一个对象，把它赋值给另一个变量的时候，python并没有拷贝这个对象，只是拷贝了这个对象的引用而已。浅拷贝：拷贝了最外围的对象本身，内部的元素都只是拷贝了一个引用而已。也就是，把对象复制一遍，但是该对象中引用的其他对象我不复
Python开发常用的三方模块如下：换个网名有点难 python 开发语言
Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
ES聚合分析原理与代码实例讲解光剑书架上的书大厂Offer收割机面试题简历程序员读书硅基计算碳基计算认知计算生物计算深度学习神经网络大数据 AIGC AGI LLM Java Python 架构设计 Agent 程序员实现财富自由
ES聚合分析原理与代码实例讲解1.背景介绍1.1问题的由来在大规模数据分析场景中，特别是在使用Elasticsearch（ES）进行数据存储和检索时，聚合分析成为了一个至关重要的功能。聚合分析允许用户对数据集进行细分和分组，以便深入探索数据的结构和模式。这在诸如实时监控、日志分析、业务洞察等领域具有广泛的应用。1.2研究现状目前，ES聚合分析已经成为现代大数据平台的核心组件之一。它支持多种类型的聚
Python编译器鹿鹿~ Python编译器 Python python 开发语言后端
嘿嘿嘿我又来了啊有些小盆友可能不知道Python其实是有编译器的，也就是PyCharm。你们可能会问到这个是干嘛的又不可以吃也不可以穿好像没有什么用，其实你还说对了这个还真的不可以吃也不可以穿，但是它用来干嘛的呢。用来编译你所打出的代码进行运行（可能这里说的有点不对但是只是个人认为）现在我们来说说PyCharm是用来干嘛的。PyCharm是一种PythonIDE，带有一整套可以帮助用户在使用Pyt
一文掌握python面向对象魔术方法（二）程序员neil python python 开发语言
接上篇：一文掌握python面向对象魔术方法（一）-CSDN博客目录六、迭代和序列化：1、__iter__(self):定义迭代器，使得类可以被for循环迭代。2、__getitem__(self,key):定义索引操作，如obj[key]。3、__setitem__(self,key,value):定义赋值操作，如obj[key]=value。4、__delitem__(self,key):定义
一文掌握python常用的list（列表）操作程序员neil python python 开发语言
目录一、创建列表1.直接创建列表：2.使用list()构造器3.使用列表推导式4.创建空列表二、访问列表元素1.列表支持通过索引访问元素，索引从0开始：2.还可以使用切片操作访问列表的一部分：三、修改列表元素四、添加元素1.append()：在末尾添加元素2.insert()：在指定位置插入元素五、删除元素1.del：删除指定位置的元素2.remove()：删除指定值的第一个匹配项3.pop()：
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
自然语言处理_tf-idf _feivirus_ 算法机器学习和数学自然语言处理 tf-idf 逆文档频率词频
importpandasaspdimportmath1.数据预处理docA="Thecatsatonmyface"docB="Thedogsatonmybed"wordsA=docA.split("")wordsB=docB.split("")wordsSet=set(wordsA).union(set(wordsB))print(wordsSet){'on','my','face','sat',
K近邻算法_分类鸢尾花数据集 _feivirus_ 算法机器学习和数学分类机器学习 K近邻
importnumpyasnpimportpandasaspdfromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitfromsklearn.metricsimportaccuracy_score1.数据预处理iris=load_iris()df=pd.DataFrame(data=ir
ztree异步加载 3213213333332132 JavaScript Ajax json Web ztree
相信新手用ztree的时候,对异步加载会有些困惑，我开始的时候也是看了API花了些时间才搞定了异步加载，在这里分享给大家。我后台代码生成的是json格式的数据，数据大家按各自的需求生成，这里只给出前端的代码。设置setting，这里只关注async属性的配置 var setting = { //异步加载配置
thirft rpc 具体调用流程 BlueSkator 中间件 rpc thrift
Thrift调用过程中，Thrift客户端和服务器之间主要用到传输层类、协议层类和处理类三个主要的核心类，这三个类的相互协作共同完成rpc的整个调用过程。在调用过程中将按照以下顺序进行协同工作：（1）将客户端程序调用的函数名和参数传递给协议层（TProtocol），协议
异或运算推导, 交换数据 dcj3sjt126com PHP 异或 ^
/* * 5 0101 * 9 1010 * * 5 ^ 5 * 0101 * 0101 * ----- * 0000 * 得出第一个规律: 相同的数进行异或, 结果是0 * * 9 ^ 5 ^ 6 * 1010 * 0101 * ---- * 1111 * * 1111 * 0110 * ---- * 1001
事件源对象周华华 JavaScript
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html xmlns="http://www.w3.org/1999/xhtml&q
MySql配置及相关命令 g21121 mysql
MySQL安装完毕后我们需要对它进行一些设置及性能优化，主要包括字符集设置，启动设置，连接优化，表优化，分区优化等等。一修改MySQL密码及用户
[简单]poi删除excel 2007超链接 53873039oycg Excel
采用解析sheet.xml方式删除超链接，缺点是要打开文件2次,代码如下: public void removeExcel2007AllHyperLink(String filePath) throws Exception { OPCPackage ocPkg = OPCPac
Struts2添加 open flash chart 云端月影
准备以下开源项目： 1. Struts 2.1.6 2. Open Flash Chart 2 Version 2 Lug Wyrm Charmer (28th, July 2009) 3. jofc2，这东西不知道是没做好还是什么意思，好像和ofc2不怎么匹配，最好下源码，有什么问题直接改。 4. log4j 用eclipse新建动态网站，取名OFC2Demo，将Struts2 l
spring包详解 aijuans spring
下载的spring包中文件及各种包众多，在项目中往往只有部分是我们必须的，如果不清楚什么时候需要什么包的话，看看下面就知道了。 aspectj目录下是在Spring框架下使用aspectj的源代码和测试程序文件。Aspectj是java最早的提供AOP的应用框架。 dist 目录下是Spring 的发布包，关于发布包下面会详细进行说明。 docs&nb
网站推广之seo概念 antonyup_2006 算法 Web 应用服务器搜索引擎 Google
持续开发一年多的b2c网站终于在08年10月23日上线了。作为开发人员的我在修改bug的同时，准备了解下网站的推广分析策略。所谓网站推广，目的在于让尽可能多的潜在用户了解并访问网站，通过网站获得有关产品和服务等信息，为最终形成购买决策提供支持。网站推广策略有很多，seo，email，adv
单例模式,sql注入,序列百合不是茶单例模式序列 sql注入预编译
序列在前面写过有关的博客,也有过总结,但是今天在做一个JDBC操作数据库的相关内容时需要使用序列创建一个自增长的字段居然不会了,所以将序列写在本篇的前面 1,序列是一个保存数据连续的增长的一种方式; 序列的创建; CREATE SEQUENCE seq_pro 2 INCREMENT BY 1 -- 每次加几个 3
Mockito单元测试实例 bijian1013 单元测试 mockito
Mockito单元测试实例： public class SettingServiceTest { private List<PersonDTO> personList = new ArrayList<PersonDTO>(); @InjectMocks private SettingPojoService settin
精通Oracle10编程SQL(9)使用游标 bijian1013 oracle 数据库 plsql
/* *使用游标 */ --显示游标 --在显式游标中使用FETCH...INTO语句 DECLARE CURSOR emp_cursor is select ename,sal from emp where deptno=1; v_ename emp.ename%TYPE; v_sal emp.sal%TYPE; begin ope
【Java语言】动态代理 bit1129 java语言
JDK接口动态代理 JDK自带的动态代理通过动态的根据接口生成字节码(实现接口的一个具体类)的方式，为接口的实现类提供代理。被代理的对象和代理对象通过InvocationHandler建立关联 package com.tom; import com.tom.model.User; import com.tom.service.IUserService;
Java通信之URL通信基础白糖_ java jdk webservice 网络协议 ITeye
java对网络通信以及提供了比较全面的jdk支持，java.net包能让程序员直接在程序中实现网络通信。在技术日新月异的现在，我们能通过很多方式实现数据通信，比如webservice、url通信、socket通信等等，今天简单介绍下URL通信。学习准备：建议首先学习java的IO基础知识 URL是统一资源定位器的简写，URL可以访问Internet和www，可以通过url
博弈Java讲义 - Java线程同步 (1) boyitech java 多线程同步锁
在并发编程中经常会碰到多个执行线程共享资源的问题。例如多个线程同时读写文件，共用数据库连接，全局的计数器等。如果不处理好多线程之间的同步问题很容易引起状态不一致或者其他的错误。同步不仅可以阻止一个线程看到对象处于不一致的状态，它还可以保证进入同步方法或者块的每个线程，都看到由同一锁保护的之前所有的修改结果。处理同步的关键就是要正确的识别临界条件（cri
java-给定字符串，删除开始和结尾处的空格，并将中间的多个连续的空格合并成一个。 bylijinnan java
public class DeleteExtraSpace { /** * 题目：给定字符串，删除开始和结尾处的空格，并将中间的多个连续的空格合并成一个。 * 方法1.用已有的String类的trim和replaceAll方法 * 方法2.全部用正则表达式，这个我不熟 * 方法3.“重新发明轮子”，从头遍历一次 */ public static v
An error has occurred.See the log file错误解决！ Kai_Ge MyEclipse
今天早上打开MyEclipse时，自动关闭！弹出An error has occurred.See the log file错误提示！很郁闷昨天启动和关闭还好着！！！打开几次依然报此错误，确定不是眼花了！打开日志文件！找到当日错误文件内容： --------------------------------------------------------------------------
[矿业与工业]修建一个空间矿床开采站要多少钱? comsci
地球上的钛金属矿藏已经接近枯竭........... 我们在冥王星的一颗卫星上面发现一些具有开采价值的矿床..... 那么,现在要编制一个预算,提交给财政部门..
解析Google Map Routes dai_lm google api
为了获得从A点到B点的路劲，经常会使用Google提供的API，例如 [url] http://maps.googleapis.com/maps/api/directions/json?origin=40.7144,-74.0060&destination=47.6063,-122.3204&sensor=false [/url] 从返回的结果上，大致可以了解应该怎么走，但
SQL还有多少“理所应当”？ datamachine sql
转贴存档，原帖地址：http://blog.chinaunix.net/uid-29242841-id-3968998.html、http://blog.chinaunix.net/uid-29242841-id-3971046.html！ ------------------------------------华丽的分割线--------------------------------
Yii使用Ajax验证时，如何设置某些字段不需要验证 dcj3sjt126com Ajax yii
经常像你注册页面,你可能非常希望只需要Ajax去验证用户名和Email,而不需要使用Ajax再去验证密码,默认如果你使用Yii 内置的ajax验证Form,例如: $form=$this->beginWidget('CActiveForm', array( 'id'=>'usuario-form',&
使用git同步网站代码 dcj3sjt126com crontab git
转自:http://ued.ctrip.com/blog/?p=3646?tn=gongxinjun.com 管理一网站，最开始使用的虚拟空间，采用提供商支持的ftp上传网站文件，后换用vps，vps可以自己搭建ftp的，但是懒得搞，直接使用scp传输文件到服务器，现在需要更新文件到服务器，使用scp真的很烦。发现本人就职的公司，采用的git+rsync的方式来管理、同步代码，遂
sql基本操作蕃薯耀 sql sql基本操作 sql常用操作
sql基本操作 >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 蕃薯耀 2015年6月1日 17:30:33 星期一 &
Spring4+Hibernate4+Atomikos3.3多数据源事务管理 hanqunfeng Hibernate4
Spring3+后不再对JTOM提供支持，所以可以改用Atomikos管理多数据源事务。Spring2.5+Hibernate3+JTOM参考：http://hanqunfeng.iteye.com/blog/1554251Atomikos官网网站：http://www.atomikos.com/ 一.pom.xml <dependency> <
jquery中两个值得注意的方法one()和trigger()方法 jackyrong trigger
在jquery中，有两个值得注意但容易忽视的方法，分别是one()方法和trigger()方法,这是从国内作者<<jquery权威指南》一书中看到不错的介绍 1） one方法 one方法的功能是让所选定的元素绑定一个仅触发一次的处理函数，格式为 one(type,${data},fn) &nb
拿工资不仅仅是让你写代码的 lampcy 工作面试咨询
这是我对团队每个新进员工说的第一件事情。这句话的意思是，我并不关心你是如何快速完成任务的，哪怕代码很差，只要它像救生艇通气门一样管用就行。这句话也是我最喜欢的座右铭之一。这个说法其实很合理：我们的工作是思考客户提出的问题，然后制定解决方案。思考第一，代码第二，公司请我们的最终目的不是写代码，而是想出解决方案。话粗理不粗。付你薪水不是让你来思考的，也不是让你来写代码的，你的目的是交付产品
架构师之对象操作----------对象的效率复制和判断是否全为空 nannan408 架构师
1.前言。如题。 2.代码。 (1)对象的复制，比spring的beanCopier在大并发下效率要高，利用net.sf.cglib.beans.BeanCopier Src src=new Src(); BeanCopier beanCopier = BeanCopier.create(Src.class, Des.class, false);
ajax 被缓存的解决方案 Rainbow702 JavaScript jquery Ajax cache 缓存
使用jquery的ajax来发送请求进行局部刷新画面，各位可能都做过。今天碰到一个奇怪的现象，就是，同一个ajax请求，在chrome中，不论发送多少次，都可以发送至服务器端，而不会被缓存。但是，换成在IE下的时候，发现，同一个ajax请求，会发生被缓存的情况，只有第一次才会被发送至服务器端，之后的不会再被发送。郁闷。解决方法如下： ① 直接使用 JQuery提供的 “cache”参数，
修改date.toLocaleString()的警告 tntxia String
我们在写程序的时候，经常要查看时间，所以我们经常会用到date.toLocaleString()，但是date.toLocaleString()是一个过时的API，代替的方法如下： package com.tntxia.htmlmaker.util; import java.text.SimpleDateFormat; import java.util.
项目完成后的小总结 xiaomiya js 总结项目
项目完成了，突然想做个总结但是有点无从下手了。做之前对于客户端给的接口很模式。然而定义好了格式要求就如此的愉快了。先说说项目主要实现的功能吧 1，按键精灵 2，获取行情数据 3，各种input输入条件判断 4，发送数据（有json格式和string格式） 5，获取预警条件列表和预警结果列表， 6，排序， 7，预警结果分页获取 8，导出文件（excel，text等） 9，修