CVPR2022:Blended Diffusion for Text-driven Editing of Natural Images
CVPR2022:Blended Diffusion for Text-driven Editing of Natural Images
Paper:https://openaccess.thecvf.com/content/CVPR2022/html/Avrahami_Blended_Diffusion_for_Text-Driven_Editing_of_Natural_Images_CVPR_2022_paper.html
Github:https://github.com/omriav/blended-diffusion
0. Conclusion
首先这篇文章我最开始看的时候有点误解了,当时没了解Guided Diffusion,以为每一步得到的损失是用来优化扩散模型UNet参数的;组会讨论后觉得这篇工作的结果在生成的区域始终有噪声,看代码之后才发现这篇工作其实是不需要训练的,基于OpenAI的Guided Diffusion预训练模型,所有的损失都作为扩散模型调整均值的一种指导;当时与这篇工作同期有GLIDE,效果明显更好,能发出来只能说是点子新吧。
后来调代码,越发觉得这篇文章没工作量,结果的瑕疵也没做优化;之后偶然发现这仨作者在六月左右已经发了Latent Blended Diffusion,有兴趣可以看看。
1. Motivation
真实图像的编辑工作主流是基于GAN模型,通过GAN Inversion实现;
首先本身基于GAN的方法,通常在训练的时候就将图像限制在了某个特定的domain中;
其次GAN Inversion的实验中表明,此方法是在重建准确性和编辑性之间需要做出取舍。
2. Goal
将编辑操作限制在某个固定区域,实现对图片的编辑,而且未编辑的部分应该与原图尽可能保持一致。
3. Contribution
1)提出了第一个使用文本驱动的,基于区域编辑真实的、多样的图像的方法:
2)保证了未改变的区域被完美保存;
4. Method
输入:给定图像x,引导的文本提示d,二进制掩码m
输出:修改的图像 x ^ \hat{x} x^
DDPM

从 X 0 → X T X_{0} \rightarrow X_{T} X0→XT,每一步可通过加噪获得,通过递推可得下式:
q ( x t ∣ x 0 ) = N ( α ˉ t x 0 , ( 1 − α ˉ t ) I ) q(x_t|x_{0})=\mathcal{N}(\sqrt{\bar{\alpha}_t}x_{0},(1-\bar{\alpha}_t)\mathbf{I}) q(xt∣x0)=N(αˉtx0,(1−αˉt)I)
即:
x t = α ˉ t x 0 + 1 − α ˉ t ε x_t = \sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\varepsilon xt=αˉtx0+1−αˉtε
Extending augmentations
在扩散过程中,由 D C L I P D_{CLIP} DCLIP损失指导的在图像像素上进行的所谓优化,可能会使得评分降低,但并不会在图像上产生高级的语义变化。
作者发现使用简单的数据增强技术便能减缓这个问题,在扩散过程的每个步骤,并不直接对于从 x t x_t xt估计得到的 x ^ 0 \hat{x}_0 x^0计算CLIP损失;而是先对 x ^ 0 \hat{x}_0 x^0进行增强操作:
class ImageAugmentations(nn.Module):
...
self.augmentations = nn.Sequential(
K.RandomAffine(degrees=15, translate=0.1, p=p, padding_mode="border"), # type: ignore
K.RandomPerspective(0.7, p=p),
)
...
augmented_batch = self.augmentations(resized_images[batch_size:])
updated_batch = torch.cat([non_augmented_batch, augmented_batch], dim=0)
...
return updated_batch
最终所得到的增强结果:
updated_batch.shape = [augmentations_number, 3, ouput_size, output_size]
在这些增强结果上计算平均梯度用于更新参数。
下图对比了有无增强操作的编辑结果:
Background preserving blending
背景损失:
D b g ( x 1 , x 2 , m ) = d ( x 1 ⊙ ( 1 − m ) , x 2 ⊙ ( 1 − m ) ) \mathcal{D}_{bg}(x_1,x_2,m)=d(x_1\odot(1-m),x_2\odot(1-m)) Dbg(x1,x2,m)=d(x1⊙(1−m),x2⊙(1−m))
其中:
d ( x 1 , x 2 ) = 1 2 ( M S E ( x 1 , x 2 ) + L P I P S ( x 1 , x 2 ) ) d(x_1,x_2) = \frac{1}{2}(MSE(x_1,x_2)+LPIPS(x_1,x_2)) d(x1,x2)=21(MSE(x1,x2)+LPIPS(x1,x2))
D b g \mathcal{D}_{bg} Dbg这是用来保护掩码之外区域的一致性。这是因为局部的 D C L I P \mathcal{D}_{CLIP} DCLIP仍会作用到全局;简单的做法是将最终结果使用掩码与输入图片结合一下,作者并没有采取这种粗暴的做法。
而是受前人工作:Burt and Adelson [7] show that two images can be blended smoothly by separately blending each level of their Laplacian pyramids. 启发,作者提出在扩散过程的每一阶段都执行blending操作,详细见Text-driven blended diffusion。简要概括,作者通过在每个扩散阶段都进行融合操作,使得最终结果中mask内外两区域的内容更为贴切(当然最终还是使用原图中的mask之外的部分)。
Local CLIP-guided diffusion
作者希望使用预训练CLIP模型作为扩散模型中的约束,从而使得编辑区域的图像能够与文本提示一致;
首先,CLIP模型训练使用的数据集为真实的图像文本对noisy latent x t x_t xt)并不能够称之为真实图像。
所以,如果想用CLIP作为约束,就需要实现从 x t x_t xt到 x 0 x_0 x0,也就是估计位于扩散逆过程的任何一阶段所产生的中间产物 x t x_t xt,所对应的真实图像 x 0 x_0 x0到底长啥样。
在DDPM中,已知 x 0 x_0 x0,可以推导得到任意阶段的 x t x_t xt;那借助这个式子同样可以得到 x 0 x_0 x0关于 x t x_t xt的表达式:
x ^ 0 = x t α ˉ t − 1 − α ˉ t ε θ ( x t , t ) α ˉ t \hat{x}_0=\frac{x_t}{\sqrt{\bar{\alpha}_t}}-\frac{\sqrt{1-\bar{\alpha}_t}\varepsilon_{\theta}(x_t,t)}{\sqrt{\bar{\alpha}_t}} x^0=αˉtxt−αˉt1−αˉtεθ(xt,t)
既然如此,便可引入CLIP作为损失函数:
D C L I P ( x , d , m ) = D c ( C L I P i m g ( x ⊙ m ) , C L I P t x t ( d ) ) \mathcal{D}_{CLIP}(x,d,m)=D_c(CLIP_{img}(x\odot m),CLIP_{txt}(d)) DCLIP(x,d,m)=Dc(CLIPimg(x⊙m),CLIPtxt(d))
其中 C L I P i m g CLIP_{img} CLIPimg, C L I P t x t CLIP_{txt} CLIPtxt分别表示CLIP的两个编码器,其输出均为512维度向量; D c D_c Dc为余弦距离;m为掩码;
整个过程伪代码如下:
for all t from k to 1 do
-
使用扩散模型预测噪声分布 N ( μ , ∑ ) \mathcal{N}(\mu,\sum) N(μ,∑)
-
得到估计的 x ^ 0 \hat{x}_0 x^0
-
进行数据增强得到 x ^ 0 , a u g \hat{x}_{0,aug} x^0,aug
-
计算 D C L I P D_{CLIP} DCLIP和 D b g D_{bg} Dbg
-
使用梯度作为指导修改噪声分布的均值,得到 x t − 1 x_{t-1} xt−1
其中 λ \lambda λ为背景保护的权重:
可以看到就算设到10,000,右边的狗子还是和原图有差异的。
Text-driven blended diffusion
为了解决背景与编辑区域不贴的问题,作者提出了在每一个扩散阶段都加入blending操作的方法。
作者的想法是,在 x 0 → x T x_0\rightarrow x_T x0→xT的过程中,每一次扩散所产生的图片 x t x_t xt (0<=t<=T),都与一个mainfold相对应,而且随着t增大,所对应的mainfold里面的图片的噪声就越多。
可以想象一下,每次扩散产生的图像 x t x_t xt,都是属于 m a i n f o l d t mainfold_t mainfoldt的,这个t不一样,就说明图片的noise程度不一样, x 0 x_0 x0最有序、 x T x_T xT最混乱。所以每一次的去噪扩散过程,都是将一个noisy image投影到一个噪音更少的mainfold上。
作者提出,把去噪扩散过程每一阶段产生的前景(mask内容),和一个与其属于同一mainfold的背景(mask外内容),通过掩码混合起来。
如何获得对应 m a i n f o l d t mainfold_t mainfoldt的背景图片呢?
x t , b g = α ˉ t x 0 + 1 − α ˉ t ε x_{t,bg} = \sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\varepsilon xt,bg=αˉtx0+1−αˉtε
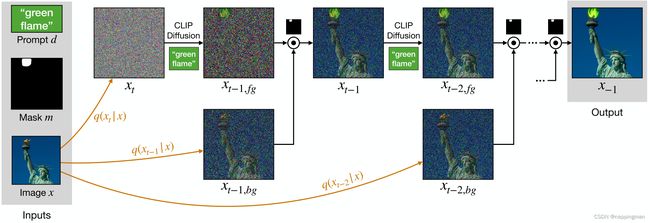
看起来就像扩散模型的两个阶段在同时进行。
整个过程伪代码如下:
for all t from k to 1 do
-
使用扩散模型预测噪声分布 N ( μ , ∑ ) \mathcal{N}(\mu,\sum) N(μ,∑)
-
得到估计的 x ^ 0 \hat{x}_0 x^0
-
进行数据增强得到一组 x ^ 0 , a u g \hat{x}_{0,aug} x^0,aug
-
在增强图片组上计算平均梯度 ∇ t e x t ∇_{text} ∇text
-
使用梯度作为指导修改噪声分布的均值,得到 x f g x_{fg} xfg
-
估计 x b g x_{bg} xbg
-
混合得到 x t − 1 x_{t-1} xt−1
注意返回的是 x − 1 x_{-1} x−1,因为最后需要用到 x 0 x_0 x0得到原始的背景。
对于相同输入的不同结果,作者使用 D C L I P \mathcal{D}_{CLIP} DCLIP作为衡量标准(不做数据增强)。
5. Experiment
Background Preserve
效果好的咱不说,生成的区域很自然,但是总感觉还没完全扩散开,掩码区域还有很多像素点比较明显。
用户测试也都觉得好——真实、背景保护、文本匹配:
由于PaintByWord这项工作没有开源,刚刚只是用PaintByWord里面的例子进行了一下对照,下面进行了更多对照:
Multiple outcomes
输出多样性
Scribble-guided editing
根据用户提供的粗糙图像进行编辑
Text-guided image extrapolation
Limitations
- 推理时间慢,半分钟推理一张图片;
- 对于输出结果的排序方法,并没有考虑整张图片,而是只对编辑区域内进行评分,导致像下面这种失败案例(1):
- 继承了
CLIP的缺点:typographic attacks,应该就像DALLE-2无法分清”红色的书在黄色的桌子上“这一类问题;






