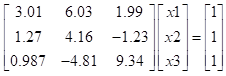奇异方程组的特解用matlab,用列主元消去法分别解方程组Ax=b，用MATLAB程序实现（最有效版）...

数值分析里面经常会涉及到用MATLAB程序实现用列主元消去法分别解方程组Ax=b

具体的方法和代码以如下方程(3x3矩阵)为例进行说明：

用列主元消去法分别解方程组Ax=b，用MATLAB程序实现：

(1)

1、 实现该方程的解的MATLAB代码可以分为两种，一种是入门级别的，只是简单地计算出这道题即可，第二种是一种通用的代码，可以实现很多3x3矩阵的方程解，写好以后只需要改不同矩阵里的元素即可算出相应的解，需要建立在对MATLAB比较熟悉的基础上，具体如下：

第一种代码实现—入门级：

A=[3.01,6.03,1.99,;1.27,4.16,-1.23,;0.987,-4.81,9.34]

A1=[3.01,6.03,1.99,1;1.27,4.16,-1.23,1;0.987,-4.81,9.34,1]

B1=A1(1,1:4)

C1=A1(2,1:4)

D1=A1(3,1:4)

E1=-1.27/3.01*B1+C1

F1=-0.987/3.01*B1+D1

p1=E1(1,2)

q1=F1(1,2)

if (abs(p1)>=abs(q1))

a1=p1

a2=q1

FF1=E1

EE1=F1

else

a1=q1

a2=p1

FF1=F1

EE1=E1

end

G1=-a2/a1*FF1+EE1

H1=[E11;FF1;G1]

J1=H1(1:3,1:3)

b1=H1(1:3,4)

x1=J1\b1

第二种代码实现如下—熟练通用级：

A=[3.01,6.03,1.99,;1.27,4.16,-1.23,;0.987,-4.81,9.34]

A1=[3.01,6.03,1.99,1;1.27,4.16,-1.23,1;0.987,-4.81,9.34,1]

B1=A1(1,1:4)

C1=A1(2,1:4)

D1=A1(3,1:4)

f1=A1(1,1)

f2=A1(2,1)

f3=A1(3,1)

if (abs(f1)>=abs(f2))

if(abs(f1)>=abs(f3))

f11=f1

E11=B1

f22=f2

E12=C1

f33=f3

E13=D1

else

f11=f3

E11=D1

f22=f1

E12=B1

f33=f2

E13=C1

end

end

if(abs(e2)>=abs(e3))

f11=f2

E11=C1

f22=f1

E12=B1

f33=f3

E13=D1

else

f11=f3

E11=D1

f22=f1

E12=B1

f33=f2

E13=C1

end

E1=-f22/f11*E11+E12

F1=-f33/f11*E11+E13

p1=E1(1,2)

q1=F1(1,2)

if (abs(p1)>=abs(q1))

a1=p1

a2=q1

FF1=E1

EE1=F1

else

a1=q1

a2=p1

FF1=F1

EE1=E1

end

G1=-a2/a1*FF1+EE1

H1=[E11;FF1;G1]

J1=H1(1:3,1:3)

b1=H1(1:3,4)

x1=J1\b1

输出结果如下：

A =

3.0100    6.0300    1.9900

1.2700    4.1600   -1.2300

0.9870   -4.8100    9.3400

A1 =

3.0100    6.0300    1.9900    1.0000

1.2700    4.1600   -1.2300    1.0000

0.9870   -4.8100    9.3400    1.0000

B1 =

3.0100    6.0300    1.9900    1.0000

C1 =

1.2700    4.1600   -1.2300    1.0000

D1 =

0.9870   -4.8100    9.3400    1.0000

f1 =

3.0100

f2 =

1.2700

f3 =

0.9870

f11 =

3.0100

E11 =

3.0100    6.0300    1.9900    1.0000

f22 =

1.2700

E12 =

1.2700    4.1600   -1.2300    1.0000

e33 =

0.9870

E13 =

0.9870   -4.8100    9.3400    1.0000

e11 =

1.2700

E11 =

1.2700    4.1600   -1.2300    1.0000

e22 =

3.0100

E12 =

3.0100    6.0300    1.9900    1.0000

e33 =

0.9870

E13 =

0.9870   -4.8100    9.3400    1.0000

E1 =

0   -3.8295    4.9052   -1.3701

F1 =

0   -8.0430   10.2959    0.2228

p1 =

-3.8295

q1 =

-8.0430

a1 =

-8.0430

a2 =

-3.8295

FF1 =

0   -8.0430   10.2959    0.2228

EE1 =

0   -3.8295    4.9052   -1.3701

G1 =

0         0    0.0030   -1.4762

H1 =

1.2700    4.1600   -1.2300    1.0000

0   -8.0430   10.2959    0.2228

0         0    0.0030   -1.4762

J1 =

1.2700    4.1600   -1.2300

0   -8.0430   10.2959

0         0    0.0030

b1 =

1.0000

0.2228

-1.4762

x1 =

1592.6

-631.9

-493.6

可以看出：两种代码的区别在于列主元方法中每一步对每一列最大主元的判断上面，第一种直接看出来，所以就用具体的数字代替了，而第二种对变量进行了一般性的定义和赋值，通过if语句进行大小判断，这样的方法会比较通用，建立在对于MATLAB熟练的基础上。

【线性代数】2-1:解方程组(Ax=b)

title: [线性代数]2-1:解方程组(Ax=b) toc: true categories: Mathematic Linear Algebra date: 2017-08-31 15:08:3 ...

列主元消去法&全主元消去法——Java实现

Gauss.java package Gauss; /** * @description TODO 父类,包含高斯列主元消去法和全主元消去法的共有属性和方法 * @author PengHao * @ ...

matlab 解方程组

1.解方程 最近有多人问如何用matlab解方程组的问题,其实在matlab中解方程组还是很方便的,例如,对于代数方程组Ax=b(A为系数矩阵,非奇异)的求解,MATLAB中有两种方法:(1)x=in ...

详解什么是平衡二叉树(AVL)(修订补充版)

详解什么是平衡二叉树(AVL)(修订补充版) 前言 Wiki:在计算机科学中,AVL树是最早被发明的自平衡二叉查找树.在AVL树中,任一节点对应的两棵子树的最大高度差为1,因此它也被称为高度平衡树.查 ...

【转】小波与小波包、小波包分解与信号重构、小波包能量特征提取 暨 小波包分解后实现按频率大小分布重新排列(Matlab 程序详解)

转:https://blog.csdn.net/cqfdcw/article/details/84995904 小波与小波包.小波包分解与信号重构.小波包能量特征提取   (Matlab 程序详解) ...

解同余式ax ≡ c(mod m)

将式子变形为 ax-c=my 可以看出原式有解当且仅当线性方程ax-my=c有解 设g = gcd(a, m) 则所有形如ax-my的数都是g的倍数 因此如果g不整除c则原方程无解. 下面假设g整除c ...

exgcd 解同余方程ax=b(%n)

ax=n(%b)  ->   ax+by=n 方程有解当且仅当 gcd(a,b) | n ( n是gcd(a,b)的倍数 ) exgcd解得 a*x0+b*y0=gcd(a,b) 记k=n/gc ...

解不定方程ax+by=m的最小解

给出方程a*x+b*y=c,其中所有数均是整数,且a,b,c是已知数,求满足那个等式的x,y值?这个方程可能有解也可能没解也可能有无穷多个解(注意:这里说的解都是整数解)? 既然如此,那我们就得找出有 ...

hdu4975 网络流解方程组(网络流+dfs判环或矩阵DP)

http://acm.hdu.edu.cn/showproblem.php?pid=4975 A simple Gaussian elimination problem. Time Limit: 20 ...

随机推荐

LeetCode Minimum Height Trees

原题链接在这里:https://leetcode.com/problems/minimum-height-trees/ 题目: For a undirected graph with tree cha ...

Objective－c——UI基础开发第十一天(UICollectionView)

一.知识点 1.UICollectionView的dataSource .delegate 2.UICollectionView多组数据和单组数据的展示 3.UICollectionView.UICo ...

atitit.编程语言 程序语言 的 工具性 和 材料性 双重性 and 语言无关性 本质

atitit.编程语言 程序语言 的 工具性 和 材料性 双重性 and 语言无关性 本质 #---语言的 工具和材料双重性 有的人说语言是个工具,有的人说语言是个材料..实际上语言同时属于两个属性. ...

UVa 1149 (贪心) Bin Packing

首先对物品按重量从小到大排序排序. 因为每个背包最多装两个物品,所以直觉上是最轻的和最重的放一起最节省空间. 考虑最轻的物品i和最重的物品j,如果ij可以放在一个包里那就放在一起. 否则的话,j只能自 ...

约束的DEFERRABLE, NOT DEFERRABLE, INITIALLY IMMEDIATE 和 INITIALLY DEFERRED

[ CONSTRAINT constraint_name ] { NOT NULL |   NULL |   CHECK ( expression ) [ NO INHERIT ] |   DEFAU ...

Ajax 缓存问题

Ajax通过GET方式请求服务器数据,Microsoft Internet Explorer浏览器下,由于缓存问题,读取的数据非最新数据,解决问题方法如下: function getData(url, ...

Java Excel 合并单元格

//合并单元格CellRangeAddress cra = new CellRangeAddress(0, 0, 0, 4);sheet.addMergedRegion(cra);

Spring Cloud Config 配置中心

请将远程配置文件的格式写对: 比如使用 *.yml 或者 *.properties yml: testconfig: testvalue properties: testconfig=testvalu ...

Django入门与实践-第12章：复用模板(完结)

http://127.0.0.1:8000/http://127.0.0.1:8000/boards/1/http://127.0.0.1:8000/boards/2/http://127.0.0.1 ...