时变多径信道的仿真
更精致的排版请查看blog
1. 仿真要求
在Matlab下进行编程，设计多径衰落信道仿真模型，具体要求如下：
-
可配置的参数包括多径数目、多径时延、各多径分量平均功率、多普勒频率扩展
-
可采用正弦波叠加或者频域滤波两种方式进行实现
-
多普勒功率谱为高斯功率谱
-
需要对信道仿真模型输出的信号的特性进行分析，绘制出其实际的信道响应特性
2. 原理分析
2.1. 多径衰落的概念及特性
多径传播是移动无线信道中信号产生衰落的主要原因。复杂的无线传播环境中，电波受到外 物的阻挡产生了反射、绕射和散射，当信号到达移动台时，已经不是原来的一路信号了，而是多个路径的多个信号的叠加。因为多路径传输造成了路径距离存在远近差别，所以发送的 一路信号在发散为多个路径后，各信号到达接收机的时间和相位都不一样。各信号按各自不 同相位叠加，相位相同的信号相加，信号增强，反之衰减，信号便产生失真。这样造成叠加 的接收信号的幅度和发送的单一信号幅度的快速巨大的差异，这称之为多径衰落。
多径衰落存在两种特性：一种是接收信号在幅度上的衰减，另一种是信号在信道上传输产生的时延扩展。具体地说，空间上，当接收端在运动时，随着距离的变化接收信号的幅度会发生衰落效应，其中接收信号的短时间的剧烈变化曲线是由于本地反射造成的，运动距离的变化对信号的平均值产生影响，运动距离的影响包括地形的变化和信号在空间传输产生的能量损耗。时间上，信号传输速度是一定的，但多径传播会导致距离的不同，由此带来信号传输时间的不一样，对同一接收端，接收同一信号在不同时间到达的合成信号，信号彼此之间存在到达时间差，即时延。这就使得接收信号相对发送信号在时间轴上产生信号宽度的增加称为时延扩展。一般来说，多径效应在信号幅度上引起的变化是模拟系统关注的重点；而它产生的时延扩展现象是数字系统考虑的重点。
2.2. 多普勒频移
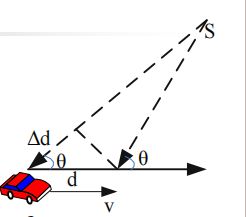
当移动台以固定速率 v v v 在长度为 d d d 的路径上运动时，收到来自远端信号 S S S 发出的信号，如图所示。无线电波从 S S S 出发，在移动台运动的两个端点分别被移动台接收时所走的路径差
Δ d = d cos θ = v Δ t cos θ \Delta d=d\cos\theta=v\Delta t \cos\theta Δd=dcosθ=vΔtcosθ
这里 Δ t \Delta t Δt是移动台从左端点运动到右端点所用的时间， θ \theta θ是两个端点与入射波的夹角。由于源端距离很远，可以假设两端点处 θ \theta θ是相同的。所以，由路程差造成的接收信号的相位变化值为
Δ ϕ = 2 π Δ d λ = 2 π v Δ t λ cos θ \Delta \phi=\frac{2\pi\Delta d}{\lambda}=\frac{2\pi v \Delta t}{\lambda} \cos\theta Δϕ=λ2πΔd=λ2πvΔtcosθ
由此可得出频率变化值，即多普勒频移 f d f_d fd为
f d = 1 2 π Δ ϕ Δ t = v λ cos θ f_d=\frac{1}{2\pi}\frac{\Delta \phi}{\Delta t}=\frac{v}{\lambda}\cos\theta fd=2π1ΔtΔϕ=λvcosθ
2.3. 多径衰落信道的分类
信号通过无线信道时所产生的多径时延、多普勒频移及信号包络所服从的各种分布等，由此导致了信号通过无线信道时经历了不同类型的衰落。接收的多路信号时延差异带来信号间的干扰，由此产生了时间色散和频率点上信号的衰落即频率色散，这两种色散可能产生4种衰落效应。总体来说，产生衰落需要信号、信道以及接收端的移动，缺一不可。概括起来这4种衰落效应是：由时间色散导致的平坦衰落和不同频段上衰落变化的频率选择性衰落；由频率色散造成的信号在频点上幅值减小，导致的快衰落效应和慢衰落效应。
2.3.1. 平坦衰落和频率选择性衰落的判断条件
理论分析结果表明当信道的频带宽度大于原始发送信号的频带带宽，且在整个带宽范围内信号增益恒定不变和相位线性变化，则接收端的信号就是平坦衰落下的信号。此种衰落，信道的多径特性不会改变接收信号的频谱分布。平坦衰落信道的条件可概括为：
B s ≪ B c , T s ≫ σ τ B_s\ll B_c,T_s\gg \sigma_{\tau} Bs≪Bc,Ts≫στ
其中 T s T_s Ts为信号周期(信号带宽 B s B_s Bs的倒数)； σ τ \sigma_{\tau} στ为信道的时延扩展； B c B_c Bc为相关带宽。
信道相当于一张门，它的带宽没有需要传送的原始信号的宽，就相当于一个高个子需要通过一张很矮的门，通过后的信号不再能保持信号原有的幅度值和相位值，他们的线性变化也无法保证，信号会表现出选择性衰落，即高个子想要通过需要弯腰才行。由信道的多径传播效应特性，信号通过信道必然存在延迟，延迟与带宽成反比，因此，我们发现在这种选择性衰落发生时信道时延会比信号周期长。从窄的信道即矮门中得到的波形是经历了衰减和时延的失真的信号。上述条件转化为公式如下：
B s > B c , T s < σ τ B_s>B_c,T_s<\sigma_{\tau} Bs>Bc,Ts<στ
通常若 T s ≤ σ τ T_s\le\sigma_{\tau} Ts≤στ，可认为这样的信道会使信号产生频率选择性衰落，在实际应用时需要根据调制方式而定。
2.3.2. 快衰落信道和慢衰落信道的判断条件
当发送端发出的原始信号的周期长度与信道的相干时间相比要大，信道多普勒扩展 B D B_D BD同样比原始发送信号的带宽 B s B_s Bs大，信道冲激响应在单个符号时间内变化迅速，接收端收到的信号会剧烈衰变，此衰落为快衰落。所以信号经历快衰落的条件是：
T s > T c , B s < B D T_s>T_c,B_s
当发送端原始信号的符号周期长度比信道的相干时间短很多，且多普勒频谱扩展 B D B_D BD比基带信号的带宽 B s B_s Bs短得多时，信道冲激信号的响应变化时间远没有传送的原始信号码元的周期时间长，这种条件下的信道属于慢衰落信道。由分析得出慢衰落的条件是：
T s ≪ T c , B s ≫ B D T_s\ll T_c,B_s\gg B_D Ts≪Tc,Bs≫BD
3. 模型建立
3.1. 随机过程模型
为刻画多径衰落信道提出了各种各样的模型，它们几乎都使用了随机过程来描述衰落。描述多径的模型有两类，离散多径模型，(有限数量的多径分量)和散射多径模型(多径分量的连续体)。在移动无线通信中，第一类模型通常用于移动无线信道的波形级的仿真，而第二类模型通常用在窄带调制的对流层信道。在两种情况下，信道都被建模为具有复低通等效响应 c ~ ( τ , t ) \tilde{c}(\tau,t) c~(τ,t)的线性时变系统。如果有N个离散的多径分量存在，则信道的输出是N个被延迟和衰减的输入信号之和。因此
y ~ ( t ) = ∑ k = 1 N ( t ) a ~ k ( t ) x ~ ( t − τ k ( t ) ) \tilde{y}(t)=\sum^{N(t)}_{k=1}\tilde{a}_k(t)\tilde{x}(t-\tau_k(t)) y~(t)=k=1∑N(t)a~k(t)x~(t−τk(t))
冲激响应 c ~ ( τ , t ) \tilde{c}(\tau,t) c~(τ,t)为
c ~ ( τ , t ) = ∑ k = 1 N ( t ) a ~ k ( t ) x ~ ( t − τ k ( t ) ) \tilde{c}(\tau,t)=\sum^{N(t)}_{k=1}\tilde{a}_k(t)\tilde{x}(t-\tau_k(t)) c~(τ,t)=k=1∑N(t)a~k(t)x~(t−τk(t))
其中N(t)为多径分量的数量，而 a k ~ ( t ) \tilde{a_k}(t) ak~(t)和 τ k ( t ) \tau_k(t) τk(t)是在t时刻第k条路径的复衰减和延迟。
如前所述，多径信道可能是时不变的。然而，对所研究的所有实际信道而言，信道可以刻画为时变的(衰落)。引起时变的原因有两个：
1.即使发射机和接收机是固定的，
环境也在变化。例如电离层的变化、植物的摇摆以及反射体和散射体的移动。
2.即使环境可能是静态的，发射机和接收机也是移动的。因此，在实际的多径信道中，N、 a k a_k ak和 τ k \tau_k τk都可能随时间随机地变化，如图所示为一个实例。
由衰落引起的接收信号随机波动可以被建模为时间t的随机过程 c ~ ( τ , t ) \tilde{c}(\tau,t) c~(τ,t)。如果接收信号是各路径的大量散射分量之和，则由中心极限定理可知， c ~ ( τ , t ) \tilde{c}(\tau,t) c~(τ,t)表示为时间的复高斯过程。在任意时刻t，概率密度函数的实部和虚部都是高斯的。这个模型意味着对于每个 τ \tau τ或 τ k \tau_k τk，信号路径是由大量不能分离的分量组成，因此， c ~ ( τ , t ) \tilde{c}(\tau,t) c~(τ,t)和 a ~ k ( t ) \tilde{a}_k(t) a~k(t)都是时间的复高斯过程。
如果 c ~ ( τ , t ) \tilde{c}(\tau,t) c~(τ,t)具有零均值，则包络 R = ∣ c ~ ( τ , t ) ∣ R=|\tilde{c}(\tau,t)| R=∣c~(τ,t)∣具有形式如下的瑞利概率密度函数
f R ( r ) = r σ 2 exp ( − r 2 2 σ 2 ) , r > 0 f_R(r)=\frac{r}{\sigma^2}\exp\left(-\frac{r^2}{2\sigma^2}\right),\quad r>0 fR(r)=σ2rexp(−2σ2r2),r>0
其中 σ 2 \sigma^2 σ2是 c ~ ( τ , t ) \tilde{c}(\tau,t) c~(τ,t)的实部和虚部的方差。
如果 c ~ ( τ , τ ) \tilde{c}(\tau,\tau) c~(τ,τ)具有非零均值，则意味着有视距非衰落的路径(称为镜像分量)存在，包络 R = ∣ c ~ ( τ , T ) ∣ R=|\tilde{c}(\tau,T)| R=∣c~(τ,T)∣具有形式如下的莱斯概率密度函数
f R ( r ) = r σ 2 I 0 ( A r σ 2 ) exp ( − r 2 + A 2 2 σ 2 ) , r > 0 f_R(r)=\frac{r}{\sigma^2}I_0\left(\frac{Ar}{\sigma^2}\right)\exp\left(-\frac{r^2+A^2}{2\sigma^2}\right),\quad r>0 fR(r)=σ2rI0(σ2Ar)exp(−2σ2r2+A2),r>0
其中A是 c ~ ( τ , t ) \tilde{c}(\tau,t) c~(τ,t)的非零均值， I 0 ( z ) I_0(z) I0(z)是修正的Bessel函数，定义如下
I 0 ( z ) = 1 2 π ∫ 0 2 π exp ( z cos ( u ) ) d u I_0(z)=\frac{1}{2\pi}\int^{2\pi}_0\exp\left(z\cos(u)\right)\mathrm{d}u I0(z)=2π1∫02πexp(zcos(u))du
比值 K = ( A 2 ) / ( σ 2 ) K=(A^2)/(\sigma^2) K=(A2)/(σ2)叫莱斯分布因子，是非衰落分量功率对衰落分量功率的比值。 K ≫ 1 K\gg 1 K≫1表示衰落不严重，而 K ≪ 1 K \ll 1 K≪1表示存在严重的衰落。
c ~ ( τ , t ) \tilde{c}(\tau,t) c~(τ,t)的概率密度函数描述了复冲激响应的瞬时值，而时变特性可以使用变量为t的随机过程适当的自相关函数或功率谱密度来建模。
3.2. 信道响应中的时变模型
要对信道的时变特性进行数学建模，可将 c ~ ( τ , t ) \tilde{c}(\tau,t) c~(τ,t)视为一个参数的广义平稳(wide
sense stationary, WSS)随机过程，其自相关函数为
R c ~ c ~ ( τ 1 , τ 2 , α ) = E [ c ~ ∗ ( τ 1 , t ) c ~ ( τ 2 , t + α ) ] R_{\tilde{c}\tilde{c}}(\tau_1,\tau_2,\alpha)=E\left[{\tilde{c}^*(\tau_1,t)\tilde{c}(\tau_2,t+\alpha)}\right] Rc~c~(τ1,τ2,α)=E[c~∗(τ1,t)c~(τ2,t+α)]
在大多数的多径信道中，假设对应于不同延迟(即不同路径)的衰或和相位偏移不相关，这种不相关散射(uncorrelated
scatterig, US)假设，有
R c ~ c ~ ( τ 1 , τ 2 , α ) = R c ~ c ~ ( τ 1 , α ) δ ( τ 1 − τ 2 ) R_{\tilde{c}\tilde{c}}(\tau_1,\tau_2,\alpha)=R_{\tilde{c}\tilde{c}}(\tau_1,\alpha)\delta(\tau_1-\tau_2) Rc~c~(τ1,τ2,α)=Rc~c~(τ1,α)δ(τ1−τ2)
上式体现了广义平稳和不相关散射两方面的假设，它经常被称为衰落的WSSUS模型，最早是由Bello提出的。用 R c ~ c ~ ( τ 1 , α ) R_{\tilde{c}\tilde{c}}(\tau_1,\alpha) Rc~c~(τ1,α)来表示自相关函数，则有
R c ~ c ~ ( τ 1 , α ) = E [ c ~ ∗ ( τ , t ) c ~ ( τ , t + α ) ] R_{\tilde{c}\tilde{c}}(\tau_1,\alpha)=E\left[{\tilde{c}^*(\tau,t)\tilde{c}(\tau,t+\alpha)}\right] Rc~c~(τ1,α)=E[c~∗(τ,t)c~(τ,t+α)]
对自相关函数作傅里叶变换，我们可以得到衰落信道的频域模型，用功率谱密度表示为
S ( τ , λ ) = F R c ~ c ~ ( τ , α ) = ∫ − ∞ ∞ R c ~ c ~ ( τ , α ) exp ( − j 2 π λ α ) d α S(\tau,\lambda)=F{R_{\tilde{c}\tilde{c}}(\tau,\alpha)}=\int_{-\infty}^{\infty}R_{\tilde{c}\tilde{c}}(\tau,\alpha)\exp(-j2\pi \lambda\alpha)\mathrm{d}\alpha S(τ,λ)=FRc~c~(τ,α)=∫−∞∞Rc~c~(τ,α)exp(−j2πλα)dα
S ( τ , λ ) S(\tau,\lambda) S(τ,λ)被称为信道的散射函数，是一个有两个自变量的函数，其中一个是时域变量(延迟),另一个是频域变量，即多普勒频率变量。散射函数以延迟和多普勒频率的函数形式，给出了一个信道平均功率输出的度量。
通过散射函数，我们可以得到信道的最重要的参數，它们将影响在信道上运行的通信系统的性能。我们从定义如下的"多径强度"曲线开始人手
p ( τ ) = R c ~ c ~ ( τ , 0 ) = E [ ∣ c ~ ( τ , t ) ∣ 2 ] p(\tau)=R_{\tilde{c}\tilde{c}}(\tau,0)=E\left[{|\tilde{c}(\tau,t)|^2}\right] p(τ)=Rc~c~(τ,0)=E[∣c~(τ,t)∣2]
上式表示作为延迟函数的平均接收功事，上式通常被称为功率-延迟曲线。可以证明， p ( τ ) p(\tau) p(τ)与散射函数通过下式相关联
p ( τ ) = ∫ − ∞ ∞ S ( τ , λ ) d λ p(\tau)=\int_{-\infty}^{\infty}S(\tau,\lambda)\mathrm{d}\lambda p(τ)=∫−∞∞S(τ,λ)dλ
刻画衰落的另一个有用的函数是多普勒功率谱，
它也可以通过下式由散射函数推导出来
S d ( λ ) = ∫ − ∞ ∞ S ( τ , λ ) d τ S_d(\lambda)=\int_{-\infty}^{\infty}S(\tau,\lambda)\mathrm{d}\tau Sd(λ)=∫−∞∞S(τ,λ)dτ
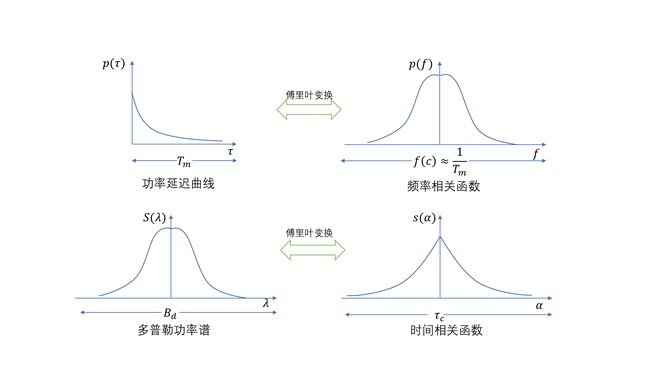
这些函数的相互关系如图所示
{width=“0.8\linewidth”}
3.3. 进一步假设
-
每个多径信号延迟、衰减互相彼此独立，不相关
-
多普勒功率谱密度模型存在多个多径分量，其中每个分量的延
迟不同，但都具有相同形状的多普勒功率谱，因此每个多径分量
的多普勒功率谱仍然是高斯的 -
每个多径信号的复衰减因子包络瑞利分布，相位均匀：即实部高斯分布，虚部也是高斯的，
实部虚部不相关。换言之，每路多径信号经过瑞利信道。 -
假设多径分量的数量和延迟结构的变化相比复衰减因子的的变化要缓慢，因此，在仿真期间可以认为是常数。
综合以上假设，可以得到第 k k k
条路径的时域相关函数 R k ( α ) = E [ a ~ k ∗ ( t ) a ~ k ( t + α ) ] R_k(\alpha)=E \left[ \tilde{a}_k^{*}(t)\tilde{a}_k(t+\alpha) \right] Rk(α)=E[a~k∗(t)a~k(t+α)]
对 R k ( α ) R_k(\alpha) Rk(α)做傅里叶变换可以得到 S k ( λ ) S_k(\lambda) Sk(λ),即多普勒功率谱。
题目限定 S k ( λ ) S_k(\lambda) Sk(λ)是高斯的，则
R k ( α ) R_k(\alpha) Rk(α)也是高斯的，因此仿真需要产生一个
时域高斯相关的随机过程的一个样本函数。可以通过图1{reference-type=“ref”
reference=“fig:gain”}来实现。
4. 仿真模型
多径衰落信道的仿真模型可以用如图所示的延时抽头线(TDL)来实现。
{width=“0.8\linewidth”}
4.1. 抽头增益过程的产生
抽头增益过程是具有高斯概率密度函数和任意功率谱密度函数的平稳随机过程。最简单的抽头增益过程模型假设它们都是不相关的复高斯过程，并具有零均值、相同功率谱密度和不同方差。在这种情况下，
如图所示，抽头增益过程可以通过对白高斯过程进行滤波来产生。
{#fig:gain width=“0.8\linewidth”}
选择滤波器传递函数，使其产生所需的多普勒功率谱密度。换句话说，选择 H ( f ) H(f) H(f)使
S g ~ g ~ ( f ) = S d ( f ) = S w ~ w ~ ( f ) ∣ H ~ ( f ) ∣ 2 = ∣ H ~ ( f ) ∣ 2 S_{\tilde{g}\tilde{g}}(f)=S_d(f)=S_{\tilde{w}\tilde{w}}(f)|\tilde{H}(f)|^2=|\tilde{H}(f)|^2 Sg~g~(f)=Sd(f)=Sw~w~(f)∣H~(f)∣2=∣H~(f)∣2
其中 S w ~ w ~ ( f ) S_{\tilde{w}\tilde{w}}(f) Sw~w~(f)是输入白噪声过程的功率谱密度，可以将其设置为1； S g ~ g ~ ( f ) S_{\tilde{g}\tilde{g}}(f) Sg~g~(f)是给定的抽头增益过程的多普勒功率谱密度，选择滤波器增益使得 g ~ ( t ) \tilde{g}(t) g~(t)具有归一化功率1。图中的静态增益 σ n \sigma_n σn说明不同抽头可以具有不同功率级或方差。如果抽头增益的功率谱密度不同，则需要使用不同的滤波器来实现不同的抽头。
5. 仿真结果
仿真设计了一个复基带信号
s ~ ( t ) = ∑ i = 1 3 exp ( 2 π f i t ) \tilde{s}(t)= \sum_{i=1}^3 \exp\left({2\pi f_i t}\right) s~(t)=i=1∑3exp(2πfit)
其中
f 1 = 1 H z , f 2 = 3 H z , f 3 = 5 H z f_1=1Hz,f_2=3Hz,f_3=5Hz f1=1Hz,f2=3Hz,f3=5Hz,多径数量 n = 10 n=10 n=10，等作为
自定义函数 c h a n n e l . m \mathrm{channel.m} channel.m文件的输入。
5.1. 快衰落
n=10;%多径数量
tau_max=0.001;%最大可能多径时延
tau=[0,tau_max*rand(1,n-1)];%随机生成n个时延
Ptau=1./(tau+1);%根据时延分配功率
f1=1;f2=3;f3=5;%设计基带频率
%设计基带复信号
singal=@(tt) exp(j*2*pi*f1*tt)+exp(j*f2*2*pi*tt)+exp(j*f3*2*pi*tt);
channel(n,tau,Ptau,1,singal);%快衰落
在这种输入参数下，将会发生快衰落，仿真结果如图2{reference-type=“ref”
reference=“fig:kaui1”},3{reference-type=“ref”
reference=“fig:kaui2”},4{reference-type=“ref”
reference=“fig:kaui3”}
{#fig:kaui1 width=“0.8\linewidth”}
{#fig:kaui2 width=“0.8\linewidth”}
{#fig:kaui3 width=“0.8\linewidth”}
-
观察图2{reference-type=“ref”
reference=“fig:kaui1”}，可以发现，复衰减因子的功率谱是高斯的，满足题目要求。 -
观察图3{reference-type=“ref”
reference=“fig:kaui2”},可以发现，信道的冲激响应在信道的符号周期内变换很快 -
观察图4{reference-type=“ref”
reference=“fig:kaui3”},可以发现，输出信号的频谱在 f 1 , f 2 , f 3 f_1,f_2,f_3 f1,f2,f3处产生
了频谱扩展，即产生了新的频谱分量
5.2. 慢衰落
channel(n,tau,Ptau,0.001,singal);%观察慢衰落
{#fig:man1 width=“0.8\linewidth”}
{#fig:man2 width=“0.8\linewidth”}
{#fig:man3 width=“0.8\linewidth”}
-
观察图5{reference-type=“ref”
reference=“fig:man1”}，可以发现，复衰减因子的功率谱几乎是一个冲激函数。 -
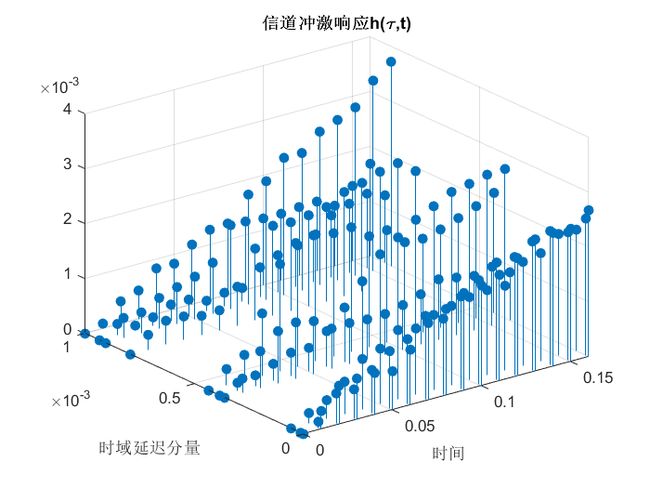
观察图3{reference-type=“ref”
reference=“fig:kaui2”},可以发现，信道的冲激响应在信道的符号周期内变换的很慢 -
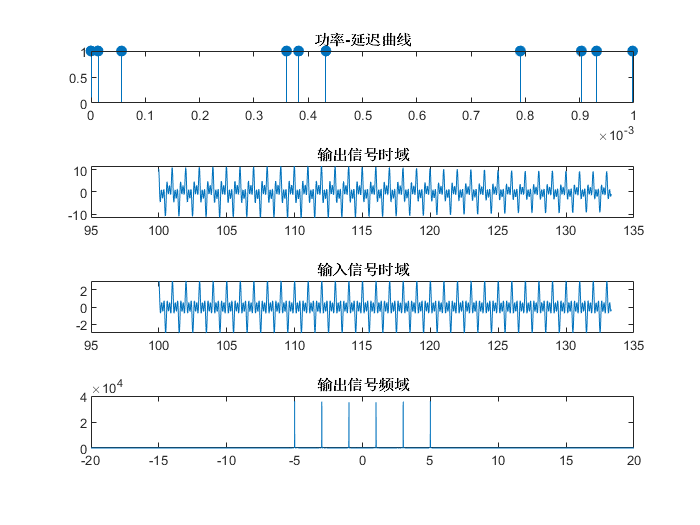
观察图4{reference-type=“ref”
reference=“fig:kaui3”},可以发现，输出信号的频谱在 f 1 , f 2 , f 3 f_1,f_2,f_3 f1,f2,f3处几乎不产生
频谱扩展，即不产生新的频谱分量 -
这些是慢衰落的一些特性
5.3. 平坦衰落
channel(n,tau,Ptau,0.01,singal);%观察平坦衰落
{#fig:tan2 width=“0.8\linewidth”}
{#fig:tan3 width=“0.8\linewidth”}
-
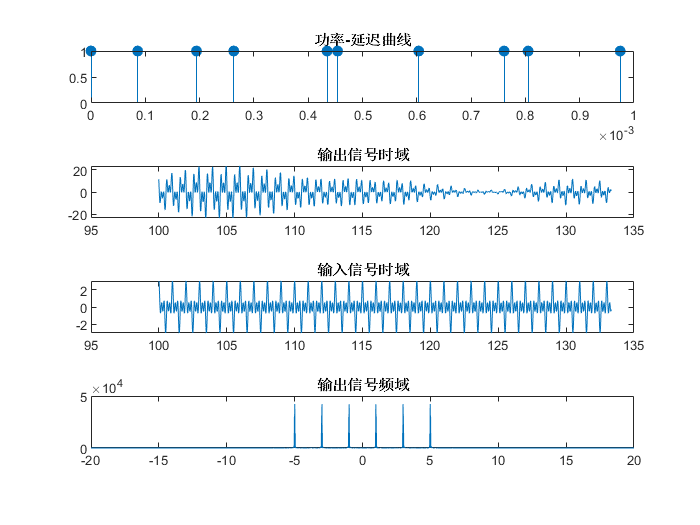
观察图8{reference-type=“ref”
reference=“fig:tan2”},可以发现，信道的冲激响应在信道的符号周期内有较大变化 -
观察图9{reference-type=“ref”
reference=“fig:tan3”},可以发现，输出信号的频谱在 f 1 , f 2 , f 3 f_1,f_2,f_3 f1,f2,f3具有相同的功率，信道
对3个频率有相等的增益。虽然频域没有发生变化，但因为信道是时变的，所以
输出信号的幅度会有剧烈的变动。 -
这些是平坦衰落的一些特性
5.4. 选择性衰落
tau_max=1;%最大可能多径时延
tau=[0,tau_max*rand(1,n-1)];%随机生成n个时延
Ptau=1./(tau+1);
channel(n,tau,Ptau,0.001,singal);%选择性衰落
{#fig:xuan2 width=“0.8\linewidth”}
{#fig:xuan3 width=“0.8\linewidth”}
-
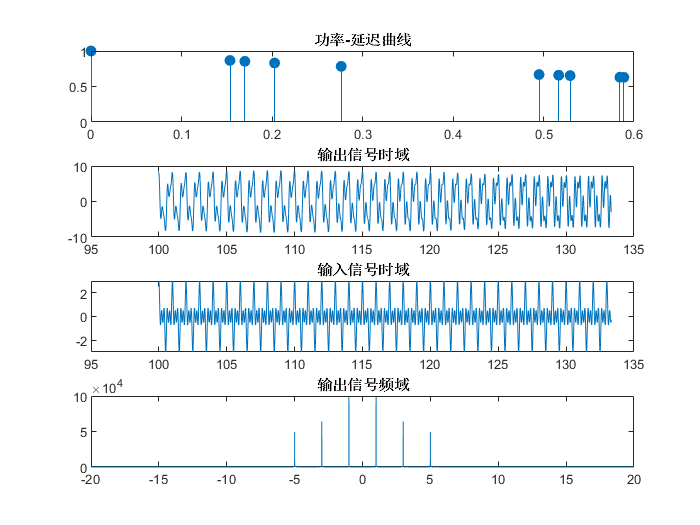
观察图11{reference-type=“ref”
reference=“fig:xuan3”},可以发现，输入信号的频谱在 f 1 , f 2 , f 3 f_1,f_2,f_3 f1,f2,f3具有相同的功率，但是输出信号的
对3个频率有不同的功率，即信道对不同频段有不同的增益。频谱发生失真，
但是输出信号时域幅度变动不大。 -
这些是选择性衰落的一些特性
6. 代码
clear
clf
n=10;%多径数量
tau_max=0.001;%最大可能多径时延
tau=[0,tau_max*rand(1,n-1)];%随机生成n个时延
Ptau=1./(tau+1);%根据时延分配功率
f1=1;f2=3;f3=5;%设计基带频率
%设计基带复信号
singal=@(tt) exp(j*2*pi*f1*tt)+exp(j*f2*2*pi*tt)+exp(j*f3*2*pi*tt);
% channel(n,tau,Ptau,1,singal);%快衰落
% channel(n,tau,Ptau,0.001,singal);%观察慢衰落
% channel(n,tau,Ptau,0.01,singal);%观察平坦衰落
tau_max=1;%最大可能多径时延
tau=[0,tau_max*rand(1,n-1)];%随机生成n个时延
Ptau=1./(tau+1);
channel(n,tau,Ptau,0.001,singal);%选择性衰落
function out=channel(n,tau,Ptau,Bd,signal_in)
% n = 1; %多径数目
% tau = ; %多径时延
% Ptau= ; %各多径分量平均功率
% Bd = ; %多普勒频谱的3dB带宽
% signal_in %输入的信号表达式，为一匿名函数
Fs=100;Ts=1/Fs;
N=2e+4;
t=(0:N-1)*1/Fs;
%%设计高斯滤波器，目的是为每一路产生相关的复衰减因子
a=sqrt(1/4*log(2)/Bd^2);%高斯滤波器参数，若Bd为3dB带宽a^2Bd^2=1/4ln2
H_gauss_fre =@(f) exp(-a^2*f.^2)/sqrt(2*pi/(2*a^2));%频域
H_gauss_time=@(t) sqrt(t)./a.*exp(-pi^2/a^2*t.^2);%时域
Gauss_t=(0:N-1)*Ts;
% sFilt = filter([0 1],[1,1], s); % Example filtered signal
%%产生n路单位复高斯白噪声
No_complex=wgn(n,N,1,'linear','complex');
%%各路的增益
K=sqrt(Ptau);
signal_out=zeros(n,N);
at=zeros(n,N);
for i=1:n
%生成第i个路径复增益的一个样本函数
at(i,:)=filter(K(i)*H_gauss_time(Gauss_t),1,No_complex(i,:));
%第i路输出
signal_out(i,:)=at(i,:).*signal_in(t-tau(i));
end
%%合并第n个路径信号
out=sum(signal_out);
%%绘图:复增益
f1=figure;
subplot 311
plot(real(No_complex(1,:)));
title('复高斯白噪音')
% at_conv=conv(No_complex,H_gauss_time(t),'same');
[r,lags]=xcorr(at(1,:),'unbiased');
% var(at)
maxlags=max(lags);
% maxlags
index1=maxlags-100:maxlags+100;
subplot 312
plot(lags(index1)*Ts,real(r(index1)));
title('高斯滤波后的波形:复衰减因子的时域自相关')
subplot 313
Fa=abs(fftshift(fft(real(r))));
Fa_normaliz=Fa/max(Fa);
index2_shift=round(20*Bd*N/Fs);
if(round(20*Bd*N/Fs)>=N)
index2_shift=N-1;
end
index2=N-index2_shift:N+index2_shift;
plot(lags(index2)*Fs/(2*N),Fa_normaliz(index2));
title('一条多径上的复衰减因子的功率谱(多普勒频谱)')
%%绘图:时变单位脉冲响应
f2=figure;
pulse=abs(at);
index3=1:round(N/1200);
stem3(t(index3),tau,pulse(:,index3),'filled')
ylabel('时域延迟分量')
xlabel('时间')
title('信道冲激响应h(\tau,t)')
%%绘图：输入输出波形
f3=figure;
index=round(N/2):round(N/2+N/6);
subplot 411
stem(tau-min(tau),Ptau,'filled')
title('功率-延迟曲线')
subplot 412
% plot(t(index),real(signal_out(1,index)))
plot(t(index),real(out(index)))
title('输出信号时域')
subplot 413
plot(t(index),real(signal_in(t(index))))
title('输入信号时域')
subplot 414
out=real(out);
[r2,lags2]=xcorr(out,'unbiased');
index414=N-round(40*N/Fs):N+round(40*N/Fs);
F_out=abs(fftshift(fft(r2)));
plot(lags2(index414)*Fs/(2*N),F_out(index414))
title('输出信号频域')
end