《数据挖掘基础》习题五
2.简单地描述下列英文缩写的含义。
(1)PAM(2)STING(3)DBSCAN
(1)PAM(Partitioning Around Medoid),围绕中心点的划分)是最早提出的k-中心点算法之一,是聚类分析算法中划分法的一个聚类方法,它选用簇中位置最中心的对象作为代表对象,试图对n个对象给出k个划分。
(2)STING(Statistical Information Grid_based Method)是一种基于网格的多分辨率聚类技术,他将空间区域划分为矩形单元。针对不同级别的分辨率,通常存在多个级别的矩形单元,这些单元形成了一个层次结构:高层的每个单元被划分为多个第一层的单元。
(3)DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一个比较有代表性的基于密度的聚类算法,它将簇定义为密度相连的点的最大集合,能够把具有足够高密度的区域划分为簇,并可在噪声的空间数据库中发现任意形状的聚类。
8.简述基于距离的聚类算法的主要特点。
基于距离的聚类算法,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。
11.给定两个对象,分别用元组(22,1,42,10),(20,0,36,8)表示。
(a)计算两个对象之间的欧氏距离。
d==[(22-20)2+(1-0)2+(42-36)2+(10-8)2](1/2)=45(1/2)=6.7
(b)计算两个对象之间的绝对距离。
d=(22-20) +(1-0) +(42-36)+(10-8)=2+1+6+2=11
13.简述划分聚类方法的主要思想。
k-means算法以k为参数,把n个对象分成k个簇,使簇内具有较高的相似度,而簇间的相似度较低。k-means算法的处理过程如下:首先,随机地选择k个对象,每个对象初始地代表了一个簇的平均值或中心,即选择K个初始质心;对剩余的每个对象,根据其与各簇中心的距离,将它赋给最近的簇;然后重新计算每个簇的平均值。这个过程不断重复,直到准则函数收敛,直到质心不发生明显的变化。通常,采用平方误差准则,误差的平方和SSE作为全局的目标函数,即最小化每个点到最近质心的欧几里得距离的平方和。此时,簇的质心就是该簇内所有数据点的平均值。
选择K个点作为初始质心repeat;
将每个点指派到最近的质心,形成K个簇;
重新计算每个簇的质心,直到簇不发生变化或达到最大迭代次数
14.请说出划分聚类与层次聚类的主要特点。
基于划分的方法简单来说就是,想象有一堆散点需要聚类,想要的聚类效果就是“类内的点都足够近,类间的点都足够远”。首先要确定这堆散点最后聚成几类,然后挑选几个点作为初始中心点,再然后依据预先定好的启发式算法给数据点做迭代重置,直到最后到达“类内的点都足够近,类间的点都足够远”的目标效果。该聚类多适用于中等体量的数据集,数据集越大,越有可能陷入局部最小。
层次聚类试图在不同层次对数据集进行划分,从而形成树形的聚类结构。数据集划分可采用“自底向上”的聚合策略,也可采用“自顶向下”的分拆策略,该方法的优点是可随时停止划分。
15.请用k-平均算法把表A5-1中的8个点聚为3个簇,假设第一次迭代选择序号1、序号4和序号7当作初始点,请给出第一次执行后的3个聚类中心以及最后的3个簇。
| 序号 | 属性1 | 属性2 | 序号 | 属性1 | 属性2 |
|---|---|---|---|---|---|
| 1 | 2 | 10 | 5 | 7 | 5 |
| 2 | 2 | 5 | 6 | 6 | 4 |
| 3 | 8 | 4 | 7 | 1 | 2 |
| 4 | 5 | 8 | 8 | 4 | 9 |

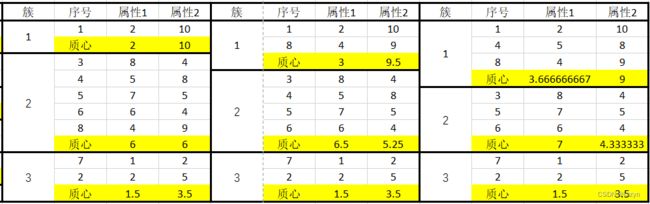 第一次:{1},{3,4,5,6,8},{2,7}
第一次:{1},{3,4,5,6,8},{2,7}
最后:{1,4,8},{2,7},{3,5,6}
18.试比较k-平均算法与k-中心点算法的特点。
K-means算法的特点:采用两阶段反复循环过程算法,结束的条件是不再有数据元素被重新分配。
k-中心点算法的特点:减轻k均值算法对孤立点的敏感性,k中心点算法不采用簇中对象的平均值作为簇中心,而选用簇中离平均值最近的对象作为簇中心。
19.简述K均值算法的主要思路。
K均值算法的主要思路:
选择聚类的个数k;
任意产生k个聚类,然后确定聚类中心,或者直接生成k个中心;
对每个点确定其聚类中心点;
再计算其聚类新中心;
重复以上步骤直到满足收敛要求(通常就是确定的中心点不再改变)。
20.简述PAM算法的主要步骤。
PAM算法的主要步骤:
(1)随机选择k个代表对象作为初始的中心点;
(2)指派每个剩余对象给离它最近的中心点所代表的簇;
(3)随机地选择一个非中心点对象y;
(4)计算用y代替中心点x的总代价s;
(5)如果s为负,则用可用y代替x,形成新的中心点;
(6)重复(2)(3)(4)(5),直到k个中心点不再发生变化。
22.在表A5-2中给定的样本上运行AGNES算法,假定算法的终止条件为3个簇,初始簇{1},{2},{3},{4},{5},{6},{7},{8}。
| 序号 | 属性1 | 属性2 | 序号 | 属性1 | 属性2 |
|---|---|---|---|---|---|
| 1 | 2 | 10 | 5 | 7 | 5 |
| 2 | 2 | 5 | 6 | 6 | 4 |
| 3 | 8 | 4 | 7 | 1 | 2 |
| 4 | 5 | 8 | 8 | 4 | 9 |
执行过程如下:
| 步骤 | 最近的簇距离 | 最近的两个簇 | 合并后的新簇 |
|---|---|---|---|
| 1 | √2 | {4},{8} | {4,8},{1},{2},{3},{5},{6},{7} |
| 2 | √2 | {3},{5} | {4,8},{3,5},{1},{2}, {6},{7} |
| 3 | √2.5 | {3,5},{6} | {4,8},{3,5,6},{1},{2},{7} |
| 4 | √7.5 | {4,8},{1} | {4,8,1},{3,5,6}, {2},{7} |
| 5 | √10 | {2},{7} | {4,8,1},{3,5,6}, {2,7} |
23.在表A5-3中给定的样本上运行DIANA算法,假定算法的终止条件为3个簇,初始簇{1,2,3,4,5,6,7,8}。
| 序号 | 属性1 | 属性2 | 序号 | 属性1 | 属性2 |
|---|---|---|---|---|---|
| 1 | 2 | 10 | 5 | 7 | 5 |
| 2 | 2 | 5 | 6 | 6 | 4 |
| 3 | 8 | 4 | 7 | 1 | 2 |
| 4 | 5 | 8 | 8 | 4 | 9 |
第一次分裂:
第一步,挑出平均相异度最大的点7,平均距离为6.49,splinter group为{7},old party为{1,2,3,4,5,6,8};
第二步,在old party中找出到最近的splinter group中的点的距离不大于到old party中最近的点的距离的点为2,splinter group为{2,7},old party为{1,3,4,5,6,8};
第三步,没有新的old party中的点分配给splinter group,此时分裂的簇数为2,未达到终止条件,继续第二次分裂。
第二次分裂:
第一步,挑出平均相异度最大的点1,平均距离为5.72,splinter group为{1},old party为{3,4,5,6,8};
第二步,没有新的old party中的点分配给splinter group,此时分裂的簇数为3,达到终止条件,结束分裂。
最终聚类结果为:{2,7},{1},{3,4,5,6,8}
24.请分析DIANA和AGNES算法的特点。
DIANA(Divisive Analysis)算法属于分裂的层次聚类,该方法是自顶向下的方法,从包含的所有点的簇开始,每一步分裂一个簇,直到仅剩下单点的簇。首先将所有的对象初始化到一个簇中,然后根据一些原则(比如最邻近的最大欧式距离),将该簇分类。直到到达用户指定的簇数目或者两个簇之间的距离超过了某个阈值。
AGNES(Agglomerative Nesting) 是凝聚的层次聚类算法,该方法是自底向上的方法,初始每个对象看做一个簇,每一步合并最相近的簇,最终形成一个簇。如果簇C1中的一个对象和簇C2中的一个对象之间的距离是所有属于不同簇的对象间欧式距离中最小的,C1和C2可能被合并。
25.简述密度聚类方法的主要思路。
密度聚类法的指导思想是,只要一个区域中的点的密度大于某个城值,就把它加到与之相近的聚类中去,这类算法能克服基于距离的算法只能发现“类圆形”聚类的缺点。
26.请举例说明DBSCAN算法的主要思想。
DBSCAN是一种基于密度的聚类算法,这类密度聚类算法一般假定类别可以通过样本分布的紧密程度决定。同一类别的样本,他们之间是紧密相连的,也就是说,在该类别任意样本周围不远处一定有同类别的样本存在。
通过将紧密相连的样本划为一类,这样就得到了一个聚类类别。通过将所有各组紧密相连的样本划为各个不同的类别,则我们就得到了最终的所有聚类类别结果。