因果分析系列4--基于python的因果图模型学习
因果分析系列4--因果图模型
- 1.因果图模型介绍
- 2.基于python绘制因果图模型
- 3.三种常见的因果图结构
-
- 3.1 链结构(chain)
- 3.2 叉结构(fork)
- 3.3 对撞结构(collider)
- 4.巩固思考示例
在上一节中,介绍了因果分析中常用的几个统计学概念:标准误差、置信区间、假设检验和p值。本节将正式介绍因果分析的基本工具之一因果图模型。
1.因果图模型介绍
图形模型作为一种描述因果关系的语言,便于彼此更好地理解和表达对因果关系的想法。
潜在结果的条件独立性是进行因果推断的主要假设之一,首先对其进行介绍:
( Y 0 , Y 1 ) ⊥ T ∣ X (Y_0, Y_1) \perp T | X (Y0,Y1)⊥T∣X
j即给定协变量 X X X,潜在结果 ( Y 0 , Y 1 ) (Y_0,Y_1 ) (Y0,Y1) 和 处理变量 T T T条件独立。鲁宾称这个条件为“可忽略性”(ignorability)。这个条件还有很多其他名字:流行病学家常常称之为“无混杂性”(unconfoundedness);经济学家常常称之为“可观测的选择机制”(selection on observables)。
下面分别对三种常见因果图模型的条件独立性规则进行介绍。
2.基于python绘制因果图模型
1.加载包
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import graphviz as gr
from matplotlib import style
import seaborn as sns
from matplotlib import pyplot as plt
style.use("fivethirtyeight")
2.因果图绘制
g = gr.Digraph("./img/DAG")
g.edge("Z", "X")
g.edge("U", "X")
g.edge("U", "Y")
g.edge("treatment", "survived")
g.edge("severeness", "survived")
g.edge("severeness", "treatment")
# g.view()
g
图中每个节点都是一个随机变量。我们使用箭头或边来显示一个变量是否导致另一个变量。在上面的第一个图形模型中,我们说Z导致X,U导致X和Y。为了给出一个更具体的例子,我们可以将其转换为药物对患者生存影响。严重程度影响治疗方式和生存状态,治疗方式也会影响生存状态。这种因果图语言明确了我们对世界的认知,能帮助我们更清楚地思考因果关系。
3.三种常见的因果图结构
理解一个图模型需要什么样的独立性和条件独立性假设是非常重要的。正如我们将看到的,独立性流经图形模型,就像水流流经小溪一样。我们可以停止这个流,也可以启用它,这取决于我们如何处理其中的变量。为了更好地理解这一点,我们研究一些常见的图形结构和示例。
3.1 链结构(chain)
首先,看这个非常简单的图。A引起B引起C,X引起Y引起Z。
g1 = gr.Digraph()
g1.edge("A", "C")
g1.edge("C", "B")
g1.edge("X", "Y")
g1.edge("Y", "Z")
g1.node("Y", "Y", color="red")
g1.edge("因果知识", "解决问题")
g1.edge("解决问题", "工作提升")
g1

上图是一个链结构(chain)因果图模型,因果关系沿着箭头的方向流动。如最右边地例子,假设因果知识是我们解决问题地唯一路径,而解决问题是我们获得工作晋升地唯一途径举。所以因果知识导致问题解决,从而导致工作晋升。我们可以在这里说,工作晋升是依赖于因果知识。因果知识越多,你升职的机会就越大。注意,依赖是对称的,尽管它没有那么直观。你升职的机会越大,说明你可能掌握因果知识的机会就越大,否则就很难升职。
现在,假设我们对中间变量施加干涉条件。此时,依赖关系被阻断。同样,如果我知道你擅长解决问题,知道因果推理并不能提供任何关于你升职机会的进一步信息。用数学符号表示:
E [ 晋 升 ∣ 解 决 问 题 , 因 果 知 识 ] = E [ 晋 升 ∣ 解 决 问 题 ] E[晋升|解决问题, 因果知识]=E[晋升|解决问题] E[晋升∣解决问题,因果知识]=E[晋升∣解决问题]
反之亦然,一旦我知道你解决问题的能力有多强,了解你的升职情况就不会进一步了解你知道因果推断的可能性有多大。
一般来说,当我们以中间变量C为条件时,从A到B的直接路径中的依赖流是阻塞的,
A ̸ ⊥ ⊥ B A \not\!\perp\!\!\!\perp B A⊥⊥B
和
A ⊥ ⊥ B ∣ C A \!\perp\!\!\!\perp B | C A⊥⊥B∣C
3.2 叉结构(fork)
叉结构(fork)是一个变量会同时影响图中的另外两个变量。在这种情况下,依赖性通过箭头向后流动,得到所谓的后门路径。我们可以关闭后门路径,通过对共同原因的限制关闭依赖。具体如下所示:
g2 = gr.Digraph()
g2.edge("C", "A")
g2.edge("C", "B")
g2.edge("X", "Y")
g2.edge("X", "Z")
g2.node("X", "X", color="red")
g2.edge("统计学", "因果推断")
g2.edge("统计学", "机器学习")
g2
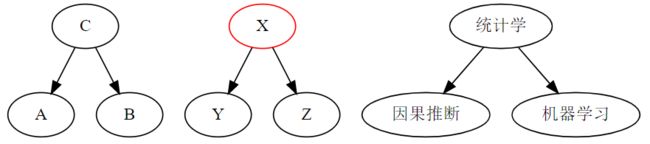
举个例子,假设你的统计学知识使你对因果推理和机器学习有了更多的了解。如果我不知道你的统计知识水平,那么知道你擅长因果推理,就知道你很可能也擅长机器学习。因为我虽然不知道你的统计知识水平,但从你的因果推理水平推断出:如果你擅长因果推理,你可能擅长统计;如果你擅长统计,很可能你也擅长机器学习。
现在,如果我以你的统计知识为条件,那么你对机器学习的了解程度就独立于你对因果推理的了解程度。因为你的统计水平已经给了我推断你机器学习技能的所有信息。在这种情况下,了解你的因果推理水平不会提供更多的信息。通常,有共同原因的两个变量是相依的,但当我们以共同原因为条件时它们是独立的。用数学符号表示为:
A ̸ ⊥ ⊥ B A \not\!\perp\!\!\!\perp B A⊥⊥B
和
A ⊥ ⊥ B ∣ C A \!\perp\!\!\!\perp B | C A⊥⊥B∣C
3.3 对撞结构(collider)
对撞结构是指两个变量的箭头均指向同一变量,即两个变量共同影响另一变量。
g3 = gr.Digraph()
g3.edge("B", "C")
g3.edge("A", "C")
g3.edge("Y", "X")
g3.edge("Z", "X")
g3.node("X", "X", color="red")
g3.edge("统计学", "工作晋升")
g3.edge("奉承", "工作晋升")
g3

上图示例中有两种方法可以升职。一是擅长统计,二是奉承老板。如果不以你的升职为条件,也就是说,我不知道你是否会升职,那么你的统计和奉承水平是独立的。换言之,了解你的统计水平,并不能说明你奉承老板的水平如何。另一方面,如果你真的升职了,此时了解你的统计水平,就可能了解你的奉承程度:如果你不擅长统计,而且确实得到了提升,那么你就更有可能知道如何奉承别人,否则不会得到晋升。相反,如果你不善于奉承别人,那一定是因为你擅长统计。这种现象有时被称为解释消失,因为一个原因已经解释了结果,使得另一个原因不太可能。
一般来说,对撞结构的条件作用反而打开了依赖路径。如果不对它进行调节,它就会关闭。用数学符号表示如下:
A ⊥ ⊥ B A \!\perp\!\!\!\perp B A⊥⊥B
和
A ̸ ⊥ ⊥ B ∣ C A \not\!\perp\!\!\!\perp B | C A⊥⊥B∣C
综合3.1至3.3的三种因果图结构,我们就可以得出一个更一般的规则。当且仅当满足以下条件时,路径才会被阻断:
1.它包含一个非对撞结构(链结构或叉结构),且已经被调节(控制);
2它包含一个尚未设置条件的对撞结构,并且没有已设置条件的子对撞结构。
4.巩固思考示例
g4 = gr.Digraph()
g4.edge("C", "A")
g4.edge("C", "B")
g4.edge("D", "A")
g4.edge("B", "E")
g4.edge("F", "E")
g4.edge("A", "G")
g4
- D ⊥ ⊥ C D \!\perp\!\!\!\perp C D⊥⊥C:它包含一个collider,且A未被控制。
- D ̸ ⊥ ⊥ C ∣ A D \not\!\perp\!\!\!\perp C| A D⊥⊥C∣A:它包含一个collider,且A已被控制。
- D ̸ ⊥ ⊥ C ∣ G D \not\!\perp\!\!\!\perp C| G D⊥⊥C∣G:它包含一个collider后代,这个collider已经被调节过了, 因为可将G看作是A的某种代理。
- A ⊥ ⊥ F A \!\perp\!\!\!\perp F A⊥⊥F:它包含一个collider,B->E<-F,E没有控制。
- A ̸ ⊥ ⊥ F ∣ E A \not\!\perp\!\!\!\perp F|E A⊥⊥F∣E:它包含一个collider,B->E<-F,E已被控制。
- A ⊥ ⊥ F ∣ E , C A \!\perp\!\!\!\perp F|E, C A⊥⊥F∣E,C:它包含一个collider,B->E<-F,E已被控制,但是它包含一个非对撞结构已被控制。条件作用于E会打开路径,但条件作用于C会再次关闭路径。
了解因果图模型使我们能够理解因果推理中出现的问题。正如我们所看到的,问题总是归结为偏差。
E [ Y ∣ T = 1 ] − E [ Y ∣ T = 0 ] = E [ Y 1 − Y 0 ∣ T = 1 ] ⏟ A T T + { E [ Y 0 ∣ T = 1 ] − E [ Y 0 ∣ T = 0 ] } ⏟ B I A S E[Y|T=1] - E[Y|T=0] = \\ \underbrace{E[Y_1 - Y_0|T=1]}_{ATT} + \underbrace{\{ E[Y_0|T=1] - E[Y_0|T=0] \}}_{BIAS} E[Y∣T=1]−E[Y∣T=0]=ATT E[Y1−Y0∣T=1]+BIAS {E[Y0∣T=1]−E[Y0∣T=0]}
下一节将针对因果分析中常见的混杂偏差和选择性偏差进行介绍。

