西北工业大学NOJ Python程序设计作业31-40
各位同学,创作不易,能否在文末打赏一瓶饮料呢?(^ _ ^)(文章末尾右下角处)
![]()
西北工业大学NOJ-Python程序设计作业题解集合:
NOJ-Python程序设计:第1季:水题(Season 1-Easy) (1-10)
NOJ-Python程序设计:第2季:小段代码(Season 2-Snippet) (11-20)
NOJ-Python程序设计:第3季:循环(Season 3-Loop) (21-30)
NOJ-Python程序设计:第4季:枚举算法(Season 4-Enumeration algorithm) (31-40)
NOJ-Python程序设计:第5季:模块化(Season 5-Modularization) (41-50)
NOJ-Python程序设计:第6季:字符串(Season 6-String) (51-60)
NOJ-Python程序设计:第7季:列表与元组(Season 7-List and Tuple) (61-70)
NOJ-Python程序设计:第8季:集合与字典(Season 8-Sets and Dictionary) (71-80)
NOJ-Python程序设计:第9季:类(Season 9-Class) (81-90)
NOJ-Python程序设计:第10季:挑战算法(Season 10-Challenges) (91-100)
第4季:枚举算法(Season 4-Enumeration algorithm)(31-40)
前置知识点
建议大概了解下述函数库的基本运用之后再完成题目会更顺利。
基本运算符:(摘自菜鸟教程)
![]()
注意区分/和//的区别
二维数组
python定义二维数组略微麻烦:
a=[[0 for i in range(1000+5)] for i in range(1000+5)]定义了一个 a [ ] [ ] a[][] a[][]大小为(1005*1005)初始值为0
math.gcd
- 语法:
math.gcd(x,y) - 返回整数x,y的最大公约数
排队过河
可能根据题目意思来分析石墩和荷叶,为了维护排队顺序,一个石墩最多2个青蛙,而荷叶有n个,另外还要再加一算上起点的。答案就是 2 n ∗ ( m + 1 ) 2^n*(m+1) 2n∗(m+1),其实也可以看数据找规律,发现这个式子。
def qpow(a,b):
a,ans=a,1
while b!=0:
if b&1:
ans=(ans*a)
b>>=1
a=(a*a)
return ans
pass
while 1:
n,m=map(int,input().split(','))
if(n==-1 and m==-1):
break
ans=qpow(2,n)*(m+1)
print(ans)
# Code By Phoenix_ZH
除法算式
一开始以为是错题,运行出来的结果比输出更多。但是观察给的图片:最后余1之前数字是3位数!然后就是枚举被除数和除数即可。
q=int(input())
for i in range(1000,9999+1):
for j in range(10,99+1):
if(i//j==q and i%j==1 and (q%10)*j>=100):#注意余数之前一定是留了3位数,所以要做判断
print(i,j,sep=' ')
# Code By Phoenix_ZH
长安
如果不考虑点P如何做?
点 ( x , y ) (x,y) (x,y)可以由点 ( x − 1 , y ) (x-1,y) (x−1,y)或者点 ( x , y − 1 ) (x,y-1) (x,y−1) 得到。
用 d p [ x ] [ y ] dp[x][y] dp[x][y]表示到达点 ( x , y ) (x,y) (x,y)的方案数,那么起始点 ( 0 , 0 ) (0,0) (0,0)的方案数就是1,即 d p [ 0 ] [ 0 ] = 1 dp[0][0]=1 dp[0][0]=1(开始瞬间就是在起点位置,所以为1)
那么 d p [ x ] [ y ] = d p [ x − 1 ] [ y ] + d p [ x ] [ y − 1 ] dp[x][y]=dp[x-1][y]+dp[x][y-1] dp[x][y]=dp[x−1][y]+dp[x][y−1])(如果是点 ( x , 0 ) (x,0) (x,0)或者 ( 0 , y ) (0,y) (0,y)那么就只有一种转移方式)
那加入点P这个条件呢?
那就保证点 ( x , y ) (x,y) (x,y)上一个节点不是点 ( p i , p j ) (p_i,p_j) (pi,pj)就好了。
但是为了转移方程式统一:保证 d p [ p i ] [ p j ] 恒为 0 就好了 dp[p_i][p_j]恒为0就好了 dp[pi][pj]恒为0就好了,其余情况和不考虑p的情况一致。
#递推:
while 1:
tx,ty,px,py=map(int,input().split(","))
if(tx==-1 and ty==-1 and px==-1 and py==-1):
break
dp=[[0 for i in range(1000+5)] for i in range(1000+5)]
dp[0][0]=1
for i in range(tx+1):
for j in range(ty+1):
if((i==0 and j==0)or(i==px and j==py)):
continue
if(i-1>=0):
dp[i][j]+=dp[i-1][j]
if(j-1>=0):
dp[i][j]+=dp[i][j-1]
# print(i,j,dp[i][j])
print(dp[tx][ty])
'''
10,10,5,5
121252
'''
# Code By Phoenix_ZH
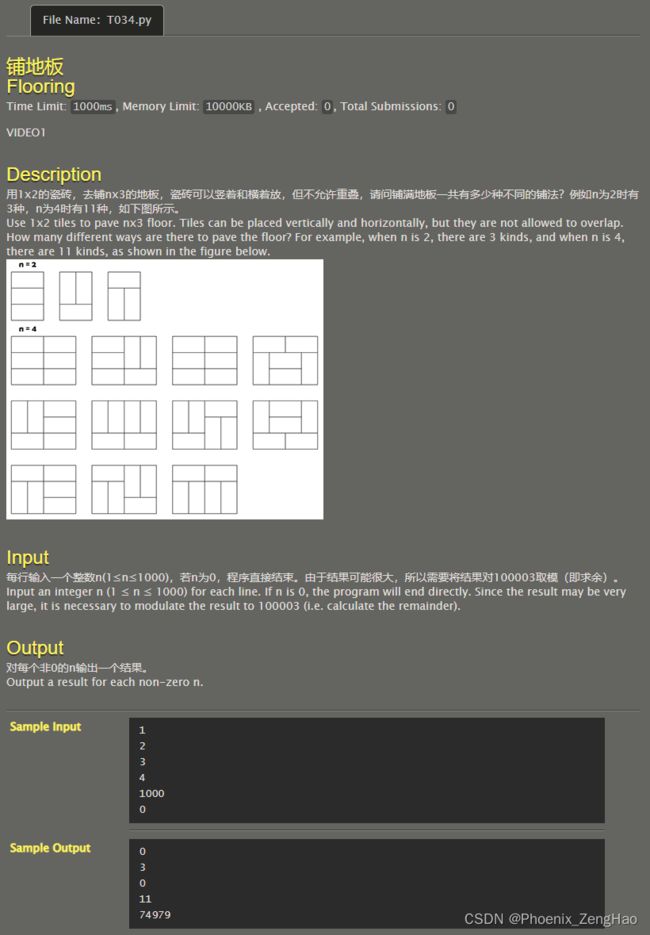
铺地板
- n如果是奇数,方案数一定为0,因为最后一列没办法拼接
- n如果是偶数,可以递推求解
这样算 d p [ 4 ] = d p [ 2 ] ∗ 4 = 12 dp[4]=dp[2]*4=12 dp[4]=dp[2]∗4=12,这显然和 d p [ 4 ] = 11 dp[4]=11 dp[4]=11不符合,原因是全竖着拼接的情况重复了,多计算了一次 d p [ i − 4 ] dp[i-4] dp[i−4],所以就是 d p [ i ] = d p [ i − 2 ] ∗ 4 − d p [ i − 1 ] ( 其中 d p [ 0 ] = 1 ) dp[i]=dp[i-2]*4-dp[i-1] (其中dp[0]=1) dp[i]=dp[i−2]∗4−dp[i−1](其中dp[0]=1)
Mod=100003
dp=[0 for i in range(10005)]
dp[0],dp[2]=1,3
for i in range(4,10000,2):
dp[i]=(dp[i-2]*4-dp[i-4])%Mod
while 1:
n=int(input())
if(n==0):
break
print(dp[n])
# Code By Phoenix_ZH
小木棍等式
'+‘和’='需要4个木棍,只剩下20个木棍,最多可以拼出10个数字,分布到左右,答案最多5位数,加数最多4个数(因为必须保证一个加数至少为0或者1,1用的木棍最少),那最简单就是 1111 + 1 = 1112 1111+1=1112 1111+1=1112需要21个木棍,那其实4位数的情况是不可能的,所以加数一定<=1000。那就直接枚举1000以内的数两两匹配即可。
a=[0 for i in range(20)]
a[0],a[1],a[2],a[3],a[4],a[5],a[6],a[7],a[8],a[9]=6,2,5,5,4,5,6,3,7,6
def cal(x):
if(x==0):
return a[0]
ans=0
while(x):
y=x%10
x//=10
ans+=a[y]
return ans
pass
n=int(input())
ans=0
for i in range(0,1000+1):
for j in range(i,1000+1):
k=i+j
if(cal(i)+cal(j)+4+cal(k)==n):
if(i!=j):
ans+=2
if(i==j):
ans+=1
print(ans)
# Code By Phoenix_ZH
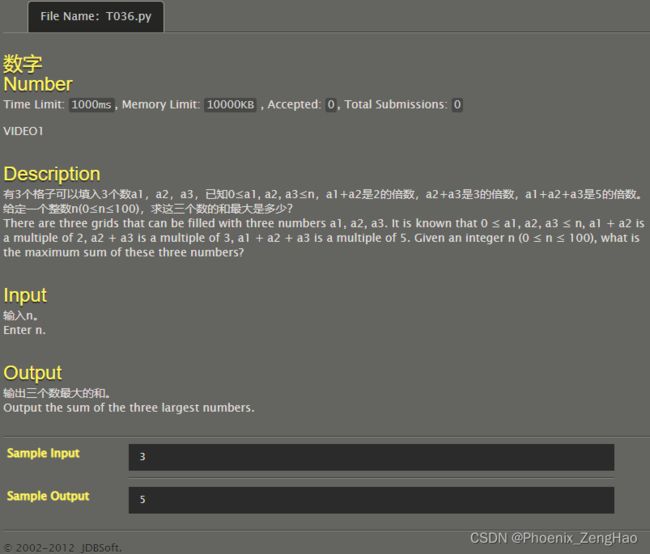
数字
这题数据有问题,题目中 n < = 100 n<=100 n<=100,但是数据存在n>100的数据
我一开始考虑了一个 O ( n 3 ) O(n^3) O(n3)的做法:枚举 a 1 , a 2 , a 3 a_1,a_2,a_3 a1,a2,a3然后统计方案数,但提交上去超时了。
于是我打表:把n<=100的情况全部统计出来:
n = int(input())
print(a[n])
for a in range(0, 100+1):
n=a
ans = 0
for i in range(n+1):
for j in range(n+1):
if((i+j) % 2):
continue
for k in range(n+1):
if((i+j) % 2 == 0 and (j+k) % 3 == 0 and (i+j+k) % 5 == 0):
ans = max(ans, i+j+k)
print("a[%d]=%d"%(a,ans))
打表结果:
a=[0 for i in range(100+5)]
a[0]=0
a[1]=0
a[2]=5
a[3]=5
a[4]=10
a[5]=10
a[6]=15
a[7]=15
a[8]=20
a[9]=25
a[10]=25
a[11]=30
a[12]=30
a[13]=35
a[14]=40
a[15]=45
a[16]=45
a[17]=50
a[18]=50
a[19]=55
a[20]=55
a[21]=60
a[22]=60
a[23]=65
a[24]=70
a[25]=70
a[26]=75
a[27]=75
a[28]=80
a[29]=85
a[30]=90
a[31]=90
a[32]=95
a[33]=95
a[34]=100
a[35]=100
a[36]=105
a[37]=105
a[38]=110
a[39]=115
a[40]=115
a[41]=120
a[42]=120
a[43]=125
a[44]=130
a[45]=135
a[46]=135
a[47]=140
a[48]=140
a[49]=145
a[50]=145
a[51]=150
a[52]=150
a[53]=155
a[54]=160
a[55]=160
a[56]=165
a[57]=165
a[58]=170
a[59]=175
a[60]=180
a[61]=180
a[62]=185
a[63]=185
a[64]=190
a[65]=190
a[66]=195
a[67]=195
a[68]=200
a[69]=205
a[70]=205
a[71]=210
a[72]=210
a[73]=215
a[74]=220
a[75]=225
a[76]=225
a[77]=230
a[78]=230
a[79]=235
a[80]=235
a[81]=240
a[82]=240
a[83]=245
a[84]=250
a[85]=250
a[86]=255
a[87]=255
a[88]=260
a[89]=265
a[90]=270
a[91]=270
a[92]=275
a[93]=275
a[94]=280
a[95]=280
a[96]=285
a[97]=285
a[98]=290
a[99]=295
a[100]=295
但是提交上去竟然RE了,说明n>100,很有可能大于了500,不然 O ( n 3 ) O(n^3) O(n3)的做法也不会超时。
然后用了一个错误的办法把它AC了:从大到小枚举 a 1 , a 2 , a 3 a_1,a_2,a_3 a1,a2,a3,一旦找到答案就输出。
但是这个做法虽然AC了,但它是错的:这样贪心 n = 99 n=99 n=99时输出了285,但实际上答案应该是295(可以打表查答案)。
n = int(input())
for i in range(n,0,-1):
for j in range(n,0,-1):
if (i+j)%2:
continue
for k in range(n,0,-1):
if((j+k)%3==0 and (i+j+k)%5==0):
print(i+j+k)
exit(0)
正解:
- a 1 + a 2 + a 3 a1 + a2 + a3 a1+a2+a3的和最大不会超过 3 ∗ n 3 * n 3∗n。由于和是 5 5 5的倍数,所以最大是 ⌊ ( 3 ∗ n ) / 5 ⌋ \lfloor(3 * n) / 5 \rfloor ⌊(3∗n)/5⌋,最小是0。因此,和的取值只能是 0 , 5 , 10 , 15 , … , ⌊ ( 3 ∗ n ) / 5 ⌋ 0, 5, 10, 15, …, \lfloor(3 * n) / 5 \rfloor 0,5,10,15,…,⌊(3∗n)/5⌋中的一个。
- 因为希望总和最大,所以考虑倒序枚举,假设总和为
top - 那么
top从 ⌊ ( 3 ∗ n ) / 5 ⌋ \lfloor(3 * n) / 5 \rfloor ⌊(3∗n)/5⌋枚举到 0 0 0 - 穷举a2, a3的可能组合,找满足如下条件的组合:
a1=top-a2-a3(a2+a3)%3==0 and (a1+a2)%2==0 and(a1+a2+a3)%5==0
- 一旦找到满足上述条件的
a1,a2,a3组合,就找到了和最大的解,正是top。输出结果后,程序无需继续寻找,可以结束了。 - 时间复杂度可以优化到
O(n^2)
n = int(input())
for top in range(3*n//5*5,-1,-5):
maxx=0
for a2 in range(n,-1,-1):
for a3 in range(n,-1,-1):
a1=min(n,top-a2-a3)
if(a1<0):
continue
if((a2+a3)%3==0 and (a1+a2)%2==0 and(a1+a2+a3)%5==0 ):
print(a1+a2+a3)
exit(0)
如果你有 O ( n l o g n ) O(nlogn) O(nlogn)之类的的做法请@我
乘方
直接进行快速幂,然后中间过程对10000取模就好了,其实也可以对10取模,总之保留个位数就够了。
def qpow(a,b,c):
a,ans=a%c,1
while b!=0:
if b&1:ans=(ans*a)%c
b>>=1
a=(a*a)%c
return ans
pass
while(1):
a,b=map(int,input().split())
if(a==0 and b==0):
break
ans=qpow(a,b,10000)
print(ans%10)
# Code By Phoenix_ZH
吃糖果
设 d p [ i ] dp[i] dp[i]为吃i个糖果的方案数。
那么 d p [ 1 ] = 1 , d p [ 2 ] = 2 , d p [ 3 ] = 3 dp[1]=1,dp[2]=2,dp[3]=3 dp[1]=1,dp[2]=2,dp[3]=3
每次可以吃一个或者两个糖果,那么当前如果总共吃了i个糖果,而这次要么吃一个要么吃两个,那么之前就有 i − 1 i-1 i−1或者 i − 2 i-2 i−2个糖果,那么方案数就是 d p [ i ] = d p [ i − 1 ] + d p [ i − 2 ] dp[i]=dp[i-1]+dp[i-2] dp[i]=dp[i−1]+dp[i−2]
dp=[0 for i in range(1000+5)]
dp[1],dp[2],dp[3]=1,2,3
for i in range(4,100):
dp[i]=dp[i-1]+dp[i-2]
while(1):
n=int(input())
if (n==0):
break
print(dp[n])
# Code By Phoenix_ZH
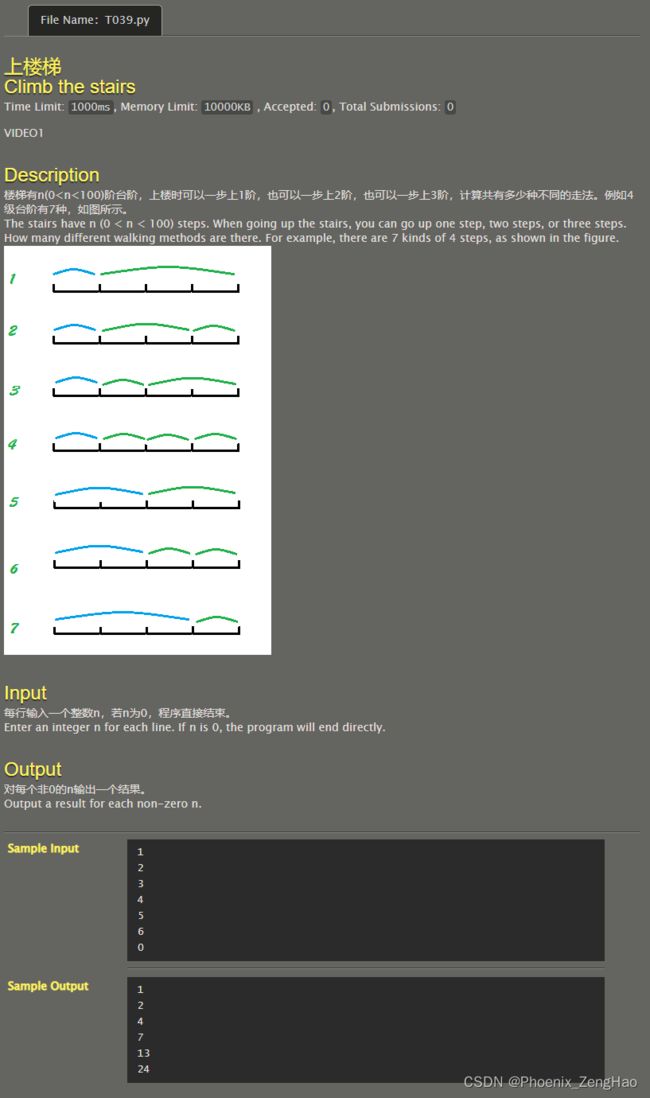
上楼梯
方法和吃糖果一模一样,只是初始化不同了,然后转移方程略有变化。
dp=[0 for i in range(1000+5)]
dp[1],dp[2],dp[3]=1,2,4
for i in range(4,500+5):
dp[i]=dp[i-1]+dp[i-2]+dp[i-3]
while(1):
n=int(input())
if(n==0):
break
print(dp[n])
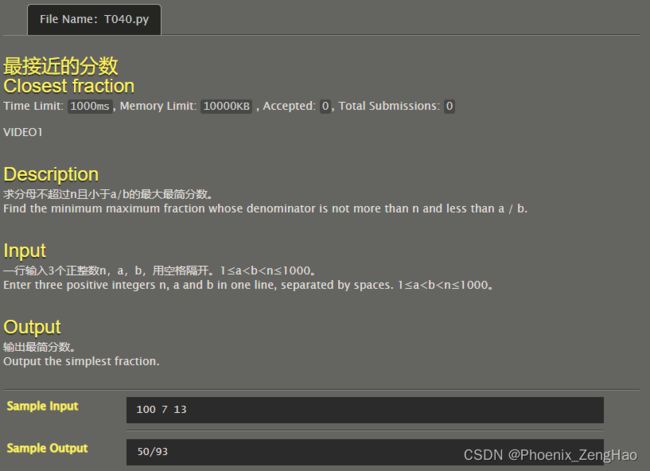
最接近的分数
直接枚举求得符合要求的最大分数即可,最后调用math.gcd函数求得最大公约数约分。
import math
n,a,b=map(int,input().split())
fz,fm=1,n
for i in range(1,n+1):
for j in range(n,0,-1):
if((a*j>b*i)and(fz*j<fm*i)):
fm,fz=j,i
g=math.gcd(fm, fz)
fm,fz=fm//g,fz//g #约分
print(fz,fm,sep='/')
# Code By Phoenix_ZH