MATLAB2016笔记（十）：曲线拟合、参数估计

---

一、曲线拟合函数

（一）概述

曲线拟合的主要功能是寻求平滑的曲线来最好的表现带有噪声的测量数据，从这些测量数据中寻求两个函数变量之间的关系或变化趋势，最后得到曲线拟合的函数表达式$y=f(x)$

拟合与插值的辨析：

插值要求通过每一个已知数据点
拟合不要求通过每一个已知数据点，因为拟合认为测量数据中包含噪声

衡量拟合数据的标准是整体数据拟合的误差最小，一般情况下，$MATLAB$的曲线拟合方法是“最小方差”，拟合曲线与已知数据之间的垂直距离最小
$${\chi }^2=\sum _i{\left[\frac{f(x_i)-y_i}{{\sigma }_i}\right]}^2$$

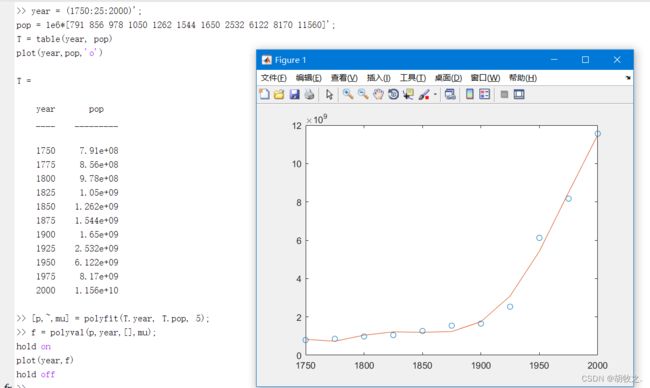
（二）多项式拟合 polyfit

返回多项式如下：$$p(x)=p_1{x}^n+p_2{x}^{n-1}+...+p_{n}x+p_{n+1}$$
其用法如下

p = polyfit(x,y,n) x、y为数据，n为多项式次数，满足平方差和最小
[p,S] = polyfit(x,y,n) S为结构体，可以在polyval中进行误差估计
[p,S,mu] = polyfit(x,y,n) mu为双元素向量，mu(1)为mean(x)，mu(2)=std(x)

（三）加权最小方差(WLS)拟合 自行编写polyfits

根据基础数据本身各自的准确度的不同，在拟合的时候给每个数据以不同的加权数值

WLS数据拟合函数——自行编写取名为polyfits

function [th,err,yi] = polyfits(x,y,N,xi,r)
% x，y：数据点系列
% N：多项式拟合的系统
% r：加权系数的逆矩阵

M = length(x);
x = x(:);
y = y(:);

% 判断调用函数的格式
if nargin == 4
    % 当调用的格式为 (x,y,N,r)
    if length(xi) == M
        r = xi;
        xi = x;
        % 当调用的格式为(x,y,N,xi)
    else r = 1;
    end;
    % 当调用格式为(x,y,N)
elseif nargin == 3
    xi = x;
    r = 1;
end
% 求解系数矩阵
A(:,N+1) = ones(M,1);
for n = N:-1:1
    A(:,n) = A(:,n+1).*x;
end
if length(r) == M
    for m =1:M
        A(m,:) = A(m,:)/r(m);
        y(m) = y(m)/r(m);
    end
end
% 计算拟合系数
th = (A\y)';
ye = polyval(th,x);
err = norm(y-ye)/norm(y);
yi = polyval(th,xi);

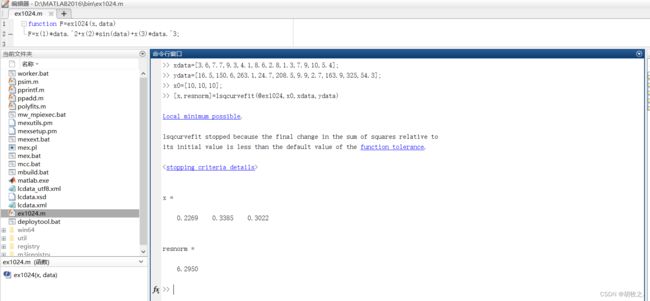
（四）非线性曲线拟合 lsqcurvefit

非线性曲线拟合是已知输入向量$xdata$、输出向量$ydata$，并且知道输入和输出的函数关系为$ydata=F(x,xdata)$，但不清楚系数向量$x$。进行曲线拟合即求$x$使得下式成立：

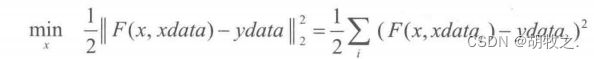
其用法如下

x = lsqcurvefit(fun,x0,xdata,ydata) 
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub)
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options) fun为拟合函数，x0为拟合函数待定参数的初值，xdata与ydata为已知的横纵坐标坐标数据点
									ub与lb为待定参数x0的上下边界（为指定则为[]），options为拟合函数的优化选项；x是待定参数的求解结果
x = lsqcurvefit(problem) 
[x,resnorm] = lsqcurvefit(___) resnorm是拟合残差的平方和，sum((fun(x,xdata)-ydata).^2)
[x,resnorm,residual,exitflag,output] = lsqcurvefit(___) residual为拟合残差，exitflag为用于描述结束条件的结束标记
														output为包含有关拟合过程信息的结构体

---

二、参数估计函数

（一）常见分布的参数分布

需要时再查看帮助文档

（二）点估计——最大似然估计 mle

百度百科——最大似然估计
最大似然法是在待估参数的可能取值范围内，挑选使似然函数值最大的那个参数值为最大似然估计量
由于最大似然估计法得到的估计量通常不仅仅满足无偏性、有效性等基本条件，还能保证其为充分统计量，所以，在点估计和区间估计中一般都推荐使用最大似然法

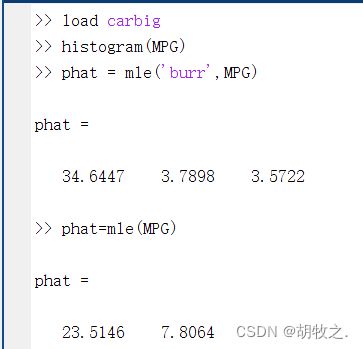
其用法如下

phat=mle('dist',data) dist为指定的分布（默认为正态分布），data为矢量中的数据样本，返回指定分布的最大似然估计

（三）点估计——矩估计法 moment

矩估计，即矩估计法，也称“矩法估计”，就是利用样本矩来估计总体中相应的参数。首先推导涉及相关参数的总体矩（即所考虑的随机变量的幂的期望值）的方程。然后取出一个样本并从这个样本估计总体矩。接着使用样本矩取代（未知的）总体矩，解出感兴趣的参数。从而得到那些参数的估计

最简单的矩估计法是用一阶样本原点矩来估计总体的期望而用二阶样本中心矩来估计总体的方差

其用法如下

m = moment(X,order)  返回由正整数order指定阶数的样本中心矩；若X为矩阵，分别对每一列进行处理

（四）区间估计 mle

求参数的区间估计，首先要求出该参数的点估计，然后构造一个含有该参数的随机变量，并根据一定的置信水平求该估计值的范围

其用法如下

[phat,pci]=mle('dist',data) 返回最大似然估计和95%置信区间
[phat,pci]=mle('dist',data,alpha) 返回100(1-alpha)%的置信区间

[phat,pci]=mle('dist',data,alpha,pl) 该形式仅用于二项分布binomial，其中pl为实验次数

---