NR 多天线传输过程 2- Scrambling -1

参考

《5G 无线系统设计与国际标准》

于威廉·斯托林斯的《数据与计算机通信》

《south western university--Scrambling》

《Prof. Hitesh Dholakiya-- Scrambling》

前言

       最近一次答辩，有同事问了LDPC 和 线性分组码有什么区别，当时只说出了应用场景不一样，以及原理不一样，回来细想一下： 处理的数据对象不一样，应用的场景也不一样.

        物理层编码： LDPC, Polar，Turbo 咬尾卷积码，每个Bit 可以认为一个channel,通过llr ,min-sum算法算出来的是一个概率,是一个连续值，基于概率去研究讨论编解码。

        MAC,PDCP,等层：

        译码后经过hard decison, 拿到的是0-1的离散比特流，传到MAC或者更上层. 上层处理的数据是离散的0-1比特流，概率信息已经丢失，基于最小汉明距离原理去讨论研究的.

    这两篇重点讲解一下scrambling,结合3GPP,以及数字编码了解一下为什么要scrambling.

1： 概述

2： Scrambling 简介

3： 3GPP 相关内容

---

一   概述

             物理层数据传输 PUSCH 和 PDSCH 经过编码和速率匹配形成码字

整个流程如下：

        

  TS38.211 里面也有详解,比如3GPP 38.211 

---

二  Scrambling 简介

    

2.1 意义

       1、减少连“0”或连“1”长度，保证接收机能提取到位定时信号。

       2、使加扰后的信号频谱更能适合基带传输。

       3、保密通信需要。

2.2 扰码分类

     根据收发双方LFSR同步方式的不同扰码分为:

    帧同步扰码（FrameSynchronous Scrambling，FSS）

   分布式抽样扰码（Distributed Sample Scrambling，DSS）

    和自同步扰码（Self Synchronous Scrambling，SSS）。

2.3 目的

          1  扰码的目的是抑制线路码中的长连“0” 和长连“1” ，便于从线路信号中提取时钟信号。

           2   扰码还可以将不同的终端或基站区分开来

          3，同时，扰码还有助于提高通信的保密性。

         4      加扰不改变信号的带宽，只是将来自不同信源的信号区分开来。这样，即使多个发射机使用相同的码字扩频也不会出现问题。

 

---

三  3GPP 相关章节

 3.1   3GPP 38.211 -6.3.1.1         Scrambling

         里面主要介绍了PUSCH Scrambling编码过程，以及相关系数

A  3GPP 38.211-6.3.1       Physical uplink shared channel（scrambling）

    

      交织后长度不变

     伪代码：

 

  入参：

  where x and y are tags：

          defined in [4, TS 38.212]

scrambling sequence   is given by clause 5.2.1. The scrambling sequence generator shall be initialized with

                         

                             

 里面mod2 作用就是模二加法,异或运算

3.2  3GPP38.212 -7.1.2             Scrambling

   里面主要结束了PBCH 编码过程。

---

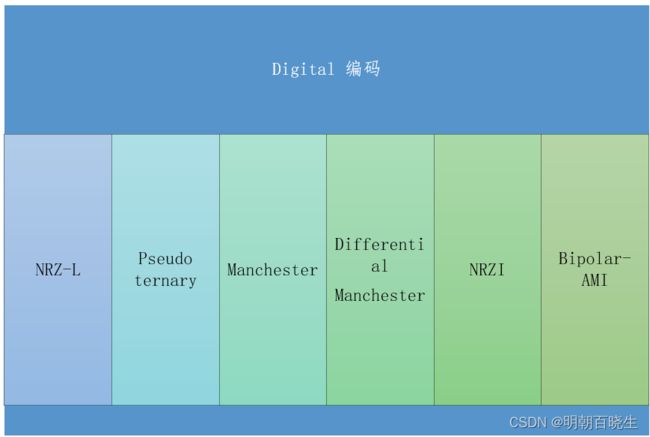
  四    数字信号编码

        

        因为scrambling跟模拟信号Clock 同步相关。

       所以这里重点讲解一下数字信号转换模拟信号的编码过程

      这里以我们发送的一个bit流data = [0,0,1,1,0,1,0,1,1,1,0,0,1] 为例

       常用的编码方案如下：

      

     4.1  NRZ-L 不归零水平(None return to zero- level)

             0  ：调制成幅度为+1的电压，

              1 ： 调制成幅度为-1的电压值

                       

               问题：

                      当遇到全0,全1 的比特流，因为接收方的clock 不同步,导致采样的时候出错.

             

   4.2 NRZI(Non return to zero invert) 不归零反相

          也叫差分编码 ：涉及到两个电压等级

            相对收发双方时钟同步:

                        侦测到电压变化，相对维持某个电压更加容易，

             问题:

             当遇到全0 的比特流，因为接收方的clock 不同步,导致采样的时候出错.

          0 ： 保持当前的电压值不变

          1：   当前的电压值反转

        data = [0,0,1,1,0,1,0,1,1,1,0,0,1] ,经过算法处理后的结果

 

     下面给出上面两种方案的代码

# -*- coding: utf-8 -*-
"""
Created on Thu Dec  8 11:26:43 2022

@author: chengxf2
"""

import numpy as np
import matplotlib.pyplot as plt
import matplotlib

def draw_voltage(data):
    
    # 将全局的字体设置为黑体
    N = len(data)
    x = np.arange(0,N)
 
    
    plt.bar(x, height=data,width=1.0,color='g',label="数字信号-voltate")
    plt.ylabel("voltate")
    plt.yticks([-1,1])
    plt.xticks(x)
    plt.legend()
    plt.show()

'''
不归零水平
0： 调制成电压值为1
1： 调制成电压值为-1
y=1-2x
'''
def NRZ_L(data):
    
    N = len(data)
    print(N)
    
    Y = []
    for x in data:
        s = 1-2*x
        Y.append(s)
    draw_voltage(Y)
    

#不归零反转
def NRZ_I(data):
    
    N = len(data)
    print(N)
    
    Y = [data[0]]
    #从-1开始
    
    prv_voltage = -1
    for i in range(N):
        
        bit = data[i]
        if 0 ==bit:
            voltage  =  prv_voltage
        else:
            voltage =  -prv_voltage
            
        Y.append(voltage)
        prv_voltage = voltage
        
   
        
        
    draw_voltage(Y)

if __name__ == "__main__":
    
    data = [0,0,1,1,0,1,0,1,1,1,0,0,1]
    

    NRZ_I(data)
    
    

     4.3 Bipolar-AMI(alternative mark inversive)

       这里涉及到三个电压等级 0,1，-1

          o :  对应的电压为0

          1： 会进行电压交替反转，

                 voltage = -pre_voltage

                 pre_voltage: 之前bit==1时候的电压值

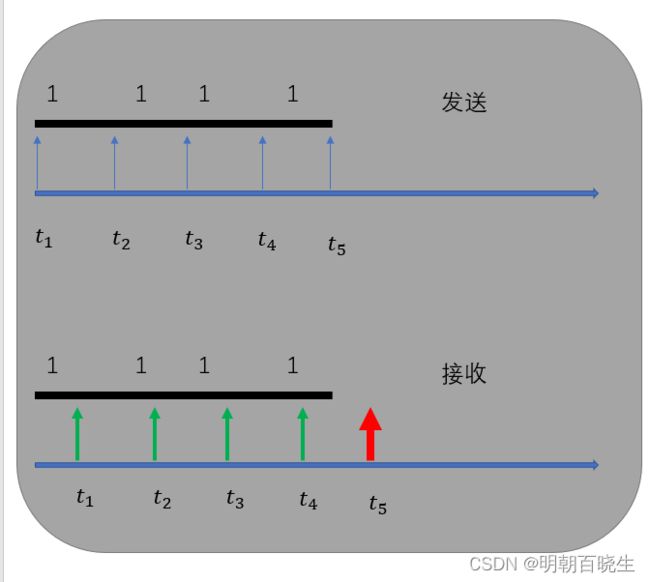
     为什么要用这种编码方式：

     涉及到收发双方的时钟同步： 如下图 发送方发送全[1 1 1 1]的bit 流

由于接收方的时钟更发送方的并不同步，会导致最后时刻再去检测出错了.

 通过AMI ，接收方可以很容易检测到voltage 变化的时候

同时根据voltage 变化的时候，进行clock 同步。

 

   问题是对全0,场景无法进行clock 同步，依然会发生错误。

# -*- coding: utf-8 -*-
"""
Created on Thu Dec  8 13:56:43 2022

@author: chengxf2
"""

import numpy as np
from pylab import *


def draw_volate(voltate):
    
   #voltate = [-1,1,1,1]
   #第一个是set_color，设置线的颜色，等价于set_c
   N = len(voltate)
   xticks = np.arange(0,N+1)
   fig = plt.figure()
   fig.suptitle('AMI 交替标记反转')
   
   line, = plt.plot(voltate,linewidth=5)
   line.set_color('g')
   
   
 
   #第二个是set_drawstyle，设置阶梯式的绘图方式，等价于set_c，效果看图
   line.set_ds('steps-mid')
    #第三个是set_linestyle，设置的是直线的类型，等价于set_ls
   #line.set_ls('--')
   
   plt.yticks([-1,0,1])
   plt.xticks(xticks)
   line.set_marker('*')
   plt.show()
   
   
def BipolarAMI():
    data = [0,0,1,1,0,1,0,1,1,1,0,0,1]
    
    Y = []
    N = len(data)
    
    pre_voltage = -1
    for i in range(N):
        bit = data[i]
        
        if 0 == bit:
            Y.append(0)
        else:
            voltage = -pre_voltage
            Y.append(voltage)
            pre_voltage = voltage
    draw_volate(Y)
            
 
 
if __name__ == "__main__":
    
    
    BipolarAMI()

4.4 pseudo ternary 编码

  跟上面相仿

 这里涉及到三个电压等级 0,1，-1

          1 : 对应的电压为0

          0： 会进行电压交替反转，

                 voltage = -pre_voltage

                 pre_voltage: 之前bit==1时候的电压值

                假设初始0的voltage 为-1

       最后两种分别为曼切斯特和差分曼切斯特编码   

 

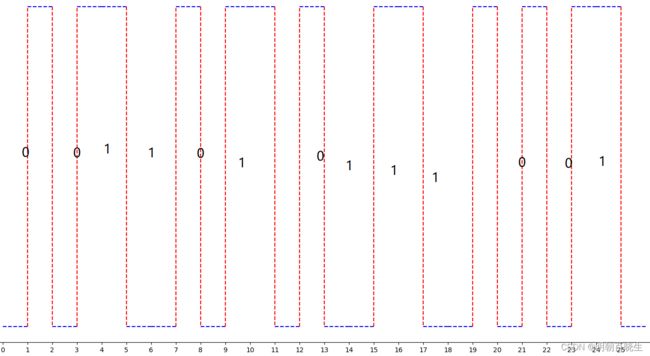
      4.5  Machester  编码（曼切斯特编码）

        0： 电压   +1, -1的跃迁过程

        1： 电压  -1，+1的跃迁过程

      增加速率开销，提供了时钟同步信息。

   

 同样 data = [0,0,1,1,0,1,0,1,1,1,0,0,1]

      

 

    4.6 different  Machester (差分曼切斯特编码)

       主要区别在区间开始的地方

       0： 区间开始的地方有个电压转变

             [-1,1]

       1:     开始voltage 跟前面保持一致

           [volate,-voltage]过程

   

 

def  show_voltage(voltage):
        
     
        fig = plt.figure()
        fig.suptitle(' Machester ')
        N = len(voltage)
        T = 1 
        
        pre_x = 0
        pre_y = -1
        
        xticks = np.arange(N)
        
        for  i in range(N):
            v = voltage[i]
         
            
            plt.plot([pre_x,i],[pre_y,v],c='g')
            plt.plot([i,i+T],[v,v],c='g')
            
            pre_x = i+T
            pre_y = v
        plt.xticks(xticks)  
        plt.yticks([-1,0,1])
        plt.legend()
        plt.show()
    
def DfMachester():
    data = [0,0,1,1,0,1,0,1,1,1,0,0,1]
    
    Y = []
    N = len(data)
    
    pre_voltage = 1
    for i in range(N):
        bit = data[i]
        
        if 0 == bit: #[1,-1]
        
            Y.append(-pre_voltage)
            Y.append(pre_voltage)
            
        else: ##[-1,1]
            Y.append(pre_voltage)
            Y.append(-pre_voltage)
            pre_voltage = -pre_voltage
    print(Y)
    show_voltage(Y)