2022.12.11 学习周报

---

摘要

本周，我阅读了一篇关于循环神经网络的论文，论文中提出了一种新的循环神经网络架构，它使得同一层中的神经元彼此独立，并且可以跨层连接。IndRNN可以很容易被调节，以防止梯度爆炸和梯度消失的问题，同时网络可以学习长期依赖性的任务。我们还可以堆叠多个IndRNN，以构建比现有RNN更深的网络，并且模型的训练具有鲁棒性。在循环神经网络的学习中，我继续学习了LSTM的相关内容，完成了对LSTM公式的前向传播和反向传播推导，以及用代码搭建了一个简单的LSTM网络。

This week, I read a paper on recurrent neural networks, in which a new architecture of recurrent neural networks is proposed, which makes neurons in the same layer independent of each other and can be connected across layers. IndRNN can be easily regulated to prevent gradient exploding and gradient vanishing problems, while the network can learn long-term dependent tasks. We can also stack multiple IndRNNs to build a deeper network than the existing RNNS, and the training of the model is robust. In the learning of Recurrent Neural Network, I continued to learn the relevant content of LSTM, completed the forward propagation and back propagation derivation of LSTM formula, and built a simple LSTM network with code.

---

文献阅读

1.题目

文献链接：Independently Recurrent Neural Network (IndRNN): Building A Longer and Deeper RNN

2.摘要

Recurrent neural networks (RNNs) have been widely used for processing sequential data. However, RNNs are commonly difficult to train due to the well-known gradient vanishing and exploding problems and hard to learn long-term patterns. Long short-term memory (LSTM) and gated recurrent unit (GRU) were developed to address these problems, but the use of hyperbolic tangent and the sigmoid action functions results in gradient decay over layers. Consequently, construction of an efficiently trainable deep network is challenging. In addition, all the neurons in an RNN layer are entangled together and their behaviour is hard to interpret. To address these problems, a new type of RNN, referred to as independently recurrent neural network (IndRNN), is proposed in this paper, where neurons in the same layer are independent of each other and they are connected across layers. We have shown that an IndRNN can be easily regulated to prevent the gradient exploding and vanishing problems while allowing the network to learn long-term dependencies. Moreover, an IndRNN can work with non-saturated activation functions such as relu (rectified linear unit) and be still trained robustly. Multiple IndRNNs can be stacked to construct a network that is deeper than the existing RNNs. Experimental results have shown that the proposed IndRNN is able to process very long sequences (over 5000 time steps), can be used to construct very deep networks (21 layers used in the experiment) and still be trained robustly. Better performances have been achieved on various tasks by using IndRNNs compared with the traditional RNN and LSTM.

3.传统RNN存在的问题

1）在传统RNN中，层内按时间展开进行参数共享，出现了梯度消失和梯度爆炸的问题。
2）在传统RNN中，层内神经元相互联系，导致难以对神经元的行为作出合理解释。
3）LSTM/GRU中使用sigmoid/tanh饱和激活函数，在解决层内梯度消失/爆炸问题时，梯度仍然会在层间衰减，因此LSTM/GRU难以做成多层网络。

4.RNN与IndRNN的对比

4.1 隐含层状态更新公式

RNN隐含层状态更新公式：

IndRNN隐含层状态更新公式：

两者对比：
1）RNN的计算公式为上一时刻的隐含层状态ht-1和权重矩阵相乘
2）IndRNN计算公式为上一时刻的隐含层状态ht-1和权重向量点乘，点乘操作使RNN 层内神经元解耦，使它们相互独立，提高神经元的可解释性。

4.2 结构示意图

4.3 IndRNN的优势

1）IndRNN将层内神经元解耦，使它们相互独立，提高神经元的可解释性。
2）IndRNN能够使用Relu等非饱和激活函数，除了解决层内和层间梯度消失/爆炸问题外，模型还具有鲁棒性，可以构建更深的网络。
3）IndRNN相比于LSTM，能处理更长（n>5000）的序列信息。

5.IndRNN的分析

5.1 RNN

RNN隐含层状态更新公式：

RNN反向传播：
设T时刻的目标函数为J，则反向传播到t时刻的梯度计算公式为：

存在的问题：
1）如果使用sigmoid或tanh激活函数，其导数的取值会小于1，与循环权重相乘构成的对角矩阵元素也会小于1，连积操作会导致梯度呈指数下降，造成梯度消失问题。
2）如果使用relu激活函数，当x>0时，relu的导数恒大于1，因此当U中有元素大于1时，则构成的对角矩阵会有大于1的元素，连积操作会导致梯度呈指数增加，造成梯度爆炸问题。

5.2 LSTM

门控单元的作用：将激活函数导数的连乘变成加法

LSTM状态更新公式：

LSTM反向传播：

上图中f(t+1)控制梯度衰减的程度：
1）当f(t+1)=1时，即使后面的项很小，梯度仍然能很好的传到上一时刻。
2）当f(t+1)=0时，上一时刻信号不受到影响。

存在的问题：
1）门控单元虽然有效缓解了梯度消失的问题，但是当序列长度过长时，梯度消失的问题仍会出现。
2）由于门控单元的存在，使计算过程无法并行，增大了计算复杂度。
3）因为多层LSTM依旧采用tanh激活函数，层与层之间的梯度消失仍未解决，所以LSTM一般为2到3层。

5.3 IndRNN的初始化

IndRNN使用ReLU作为激活函数，将权重矩阵初始化为单位矩阵，将偏置初始化为0。

5.4 梯度截断

方法：在反向传播中，人为设定传递多少步，即可看作设定对角矩阵连乘几次，强行拉回到正常值，再进行梯度下降。
问题：加入了人为因素，最后得到的值不一定准确。

5.5 IndRNN

IndRNN隐含层状态更新公式：

反向传播：

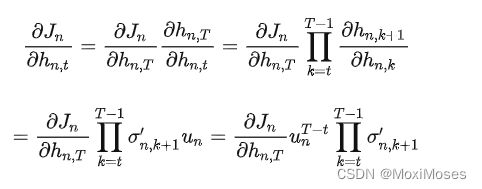
从上图中可以看出，此时的连积操作已经不再是矩阵操作，而是激活函数的导数与循环权重系数独立起来。我们只需要对un约束到合适的范围，就可以避免梯度问题。

神经元之间的相互连接依赖于层间交互来完成。也就是说，下一层的神将元会接受上一层所有神经元的输出作为输入，相当于全连接层。

IndRNN可实现多层堆叠。因为在多层堆叠结构中，层间交互是全连接方式，因此可以进行改进，比如改全连接方式为CNN连接，也可以引入BN、残差连接等。

6.实验结果

实验在三个评估RNN模型的常用任务上进行，以验证IndRNN的长程记忆能力和深层网络训练的可行性，此为验证性实验，然后在骨骼动作识别任务上进行预测，此为实验性实验。

6.1 Adding Problem

实验中输入两个序列，第一个序列是在（0, 1）范围内均匀采样，第二个序列由两个数字组成，分别为1和0。
实验序列长度：100，500和1000
其中：均方误差（MSE）用作目标函数和Adam优化方法用于训练

从上图中可以看出，IRNN和LSTM只能处理500步到1000步的序列，而IndRNN可以轻松处理时间跨度为5000步的序列数据。

6.2 Sequential MNIST Classification

实验中输入一串MINIST像素点的数据，然后进行分类。pMINIST 是在MINIST任务上增加了难度，对像素点数据进行了置换。

6.3 Language Modeling

实验在字符级别PTB数据集上进行语言模型的评估。在该任务中，为了验证IndRNN可以构造深层网络，论文中给出了21层IndRNN的训练以及结果，对比6层IndRNN的结果，得到加深后的IndRNN表现更好。

6.4 Skeleton Based Action Recognition

实验使用了NTU RGB+D数据库，是目前为止最大的基于骨骼的动作识别数据库。

7.结论

论文中提出了IndRNN，其中每一层的神经元彼此独立，并且有效地解决了梯度消失和梯度爆炸的问题。与现有的RNN模型相比，IndRNN比LSTM和GRU能更好地处理更长的序列。IndRNN可以被堆叠以构建深度网络，特别是与残差连接相结合，使得深度网络训练具有鲁棒性。

深度学习

LSTM公式推导

1.前向传播

2.反向传播

反向传播需要定义c, h的反向传播误差量，t代表第t个时间步，h是隐藏层，c是LSTM存储长期记忆信息的路径。

计算每一时间步中h的反向传播误差值

同理，可以用每一个时间步中h的反向传播值计算出c中每一个时间步的反向传播值

更新遗忘门各个时间步的权重值和偏差值

更新输入门各个时间步的权重值和偏差值

更新输出门各个时间步的权重值和偏差值

LSTM代码实现

1）nn.lstm()的输入为(序列长度，batch，输入维数)
2）使用batch_first=True，把输入变成(batch，序列长度，输入维度)，这里序列长度指的是一句话的单词数目，而且batch_first=True会改变输出的维度顺序。
3）x是单词的索引列表，size为len(x)。
4）embedding之后，x的size为(len(x), n_dim)。
5）unsqueeze之后，x的size为(1, len(x), n_dim)，其中1在下一行程序的lstm中被当做是batchsize，len(x)被当做序列长度。
6）lstm的隐藏层输出，x的size为(1, len(x), n_hidden)，因为定义lstm网络时用了batch_first=True，所以1在第一维，如果batch_first=False，则len(x)会在第一维。
7）squeeze之后，x的size为(len(x), n_hidden)，在下一行的linear层中，len(x)被当做是batchsize。
8）linear层之后，x的size为(len(x), n_tag)。
9）y的size为(len(x), n_tag)。

import torch
import torch.nn.functional as F
from torch import nn


class LSTM(nn.Module):
    def __init__(self, n_word, n_dim, n_hidden, n_tag):
        super(LSTM, self).__init__()
        self.word_embedding = nn.Embedding(n_word, n_dim)
        self.lstm = nn.LSTM(n_dim, n_hidden, batch_first=True)
        self.linear = nn.Linear(n_hidden, n_tag)

    def forward(self, x): 
        x = self.word_embedding(x)
        x = x.unsqueeze(0)
        x, _ = self.lstm(x)
        x = x.squeeze(0)
        x = self.linear(x)
        y = F.log_softmax(x, dim=1)
        return y

---

总结

本周，我继续学习了循环神经网络的相关内容，完成了对LSTM公式推导和代码练习。下周我会深入地学习GRU的内容，掌握其中的原理。由于下周将要进入期末考试阶段，我会花更多的时间去学习课程内容，以便更好地完成期末考试。