因果推断学习笔记一
一、因果推断
本次课程是《Introduction to Causal Inference》这门课程的第一次课程,主要介绍跟因果推断相关的一些基本知识。这门课程会涉及到一些跟统计和机器学习相关的背景知识。
因果推断是在推断一个变量( X X X)对另外一个变量( Y Y Y)的影响。它的使用场景非常广泛。比如判断某种治疗方式对于减轻疾病是否有用; 判断哪种环保政策对减少排放更有用;判断社交媒体是不是导致社会成员的心理状况恶化;判断最近的疫情对广州/深圳的影响有多大,判断整个COVID-19对网约车的影响有多大;…… 因果推断在企业里可以直接应用在与决策相关的部分。比如,判断某个新的策略是不是能够有效提升GMV;判断节假日的某个运营活动是否能够有效拉动司机的出车意愿;在日常运营中,判断给某个城市的B补/C补额度如何分配才能最大化这个城市的完单;在广告投放中,某个广告展现是否有效刺激了用户购买产品的意愿……

我们首先从一个例子出发,来了解下因果推断为什么不像想象中那么简单。我们会介绍辛普森悖论的一个例子,并在其中说明因果假设在我们判断因果效应时十分重要。第二部分会介绍association, correlatioin 和causation的关系, 会详细说明为什么association/correlation不能表示causation。第三部分会引入潜在结果的概念来进行因果效应的计算;最后一部分会介绍在只有观测数据,没有实验数据时,如何进行因果推断。

二、辛普森悖论
先从一个辛普森悖论的例子出发,假设你是制定国家防疫政策的工作人员,有一种新的疾病COVID-27,有两种治疗方法A(0)和B(1)经过了前期实验,这时你手头有一些关于疾病以及治疗方法A和B的一些数据,你需要为国家和人民找到一个适合的治疗方法。对治疗方法唯一的考量因素就是让死亡人数尽量少,或者说让尽量多的人生存下来。在这个例子里,还有一个重要的事实,Treatment B比Treatment A更稀缺。在这个实验里,每个病人在治疗开展时,都有一维二值变量来描述他当时病情的严重程度:轻微(0),严重(1)。对每个病人都有一个Outcome Y,表示病人活下来了(0)或者死亡了(1)。这个例子里的所有相关变量都采用了二值变量。但是在我们实际的使用过程中,并不仅仅只处理二值变量有关的因果效应。使用二值变量是因为二值变量理解起来更容易。 在我们实际的使用过程中,经常会碰到连续Treatment或者多Treatment的因果效应。

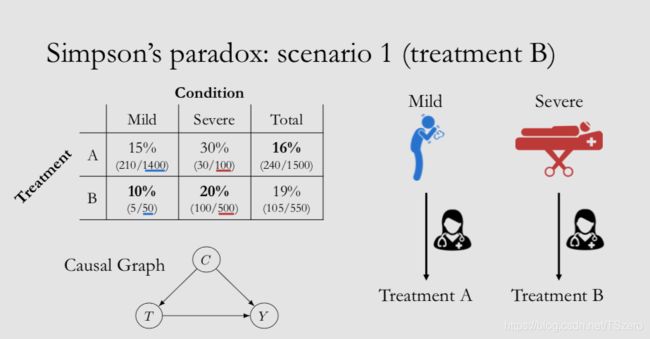
这张图就是这次试验数据的汇总。在使用了治疗A的人群中,16%的病人死亡,1500人接受治疗,其中240人死亡。在使用了治疗B的人群中,19%的病人死亡。从汇总数据上看,治疗A要比治疗B好一些,因为死亡比例减少了3% 。

如果我们对数据进行分情况讨论,对于症状轻微的病人而言,如果采用了治疗A,死亡率是15%,如果采用治疗B,死亡率是10%, 从这个数据上看, 治疗B的效果更好一些。对于症状严重的病人也是一样,仍然是治疗B的效果会更好。那么问题来了, 数字为何翻转了?也就是说只查看总体时,治疗A看起来更好;查看每个子组时,治疗B更好。这就是辛普森悖论。在A组计算总体死亡率0.16的这个式子中,轻症患者的死亡率的权重较大,重症患者的死亡率的权重较小。这是因为大多数接受治疗A的人群中,轻症患者的比例较大。所以总体死亡率0.16主要是因为轻症死亡率0.15在其中占的比例非常大。对于B组数据而言,重症患者的比例非常高啊,达到了500/550。所以0.19主要是因为重症死亡率0.20在其中占的比例非常大(500/550)。 辛普森悖论主要来自于这种不平等的加权(unequal weighting)。 治疗A中的大多数病人是轻症,治疗B中的大多数病人是重症。重症病人比轻症病人更容易死亡。
虽然我们知道了辛普森悖论的来源,通过对式子进行拆分知道数字为什么反转,但是我们还是不知道该采用哪种治疗方式。这个问题的答案很大程度上取决于因果结构。
场景1: Condition(病情)是Treatment(治疗)的原因,而且病情和治疗一起导致了结果。在这种情况下,选择治疗B效果更好。我们假设一种治疗方案的分配过程:当病人来找医生看病时,如果病人症状较轻,医生选择治疗A给病人,因为他想保留更稀缺的治疗方案B给重症病人。所以在患有轻症的1450人中,有1400人被分配到了治疗A组,仅有50人被分配到了治疗B组。如果重症病人来找医生看病,医生更倾向于分配治疗方案B。这就能解释为什么大多数重症病人(500/600)被分配了治疗B。 在这种情况下,我们认为Treatment B的治疗效果更好,是因为在与Treatment A比较的过程中,Treatment B被“不公平”的分配给了患有严重疾病的人。当病情被作为分配治疗方案的原因时,必须针对病情做调整。
场景2: 在这个场景下,治疗手段是引起病情不同的原因,此时,Treatment A是更好的治疗手段。在因果图中,Treatment是C和Y的原因,C是Y的原因,但不是T的原因。我们再假设一种治疗方案的分配过程,来说明Treatment A是更好的治疗手段。当病人来找医生看病时,医生随机的给病人分配治疗方案A或者B。由于治疗手段B更稀缺,所以在全量2050个病人中,1500个人分配了治疗方案A,仅有550个人分配了B。 然而由于B非常稀少,所以被分配到B组的人群需要等待很长时间才能够真正接受治疗B。 病人在等待的过程中导致病情更为恶化,所以B组中的重症比例更高。然而对于分配给治疗组A的病人来说,A非常充足,病人不需要等待,在病人还处于轻症时,就能够给予及时的治疗,所以A组中的轻症比例更高。在这种情况下,我们选择A,是因为Treatment B的选择会导致病情的恶化,进而影响死亡率。此时,讨论哪种治疗方案更优,需要看总人数。方案B不被选择,不是因为方案B的治疗方案本身更差,而是由于它的稀缺性会让病情恶化。

总结一下,当Condition是选择治疗的原因时,我们更喜欢B;当治疗是Condition的原因时,我们更喜欢A。在决策A/B哪个更好时,因果结构是关键。
这个例子给我们一个非常重要的启示:在进行因果推断时,数据很重要,数据的产生过程同样重要。这与我们做相关性学习时关注的重点不一样。
对于机器学习领域的同学们来说,换句话说就是,prediction不是causation。 Brady的课程内容中没有对correlation和causation进行区分,后面我们会引申一下correlation与causation的区别。
三、prediction与prediction
这里是另一个例子,在这份数据中,我们发现大多数头天晚上穿着鞋子睡觉的人,第二天早上醒来时会伴随头痛。而且大多数头天晚上没有穿鞋子睡觉的人,早上醒来时并不会头痛。于是,我们认为穿鞋子睡觉跟早上起来头痛这两件事情之间有着强相关性(association)。如果第二天早上头痛的人在看到这份数据之后可能会想“哎,那我不应该穿鞋睡觉的,那样我就不会头痛了”。 但是,这份数据背后还有一个隐藏的原因,那就是大多数晚上穿鞋子睡觉的人喝多了,同时这些人在早上起来后头疼。然后我们就知道穿鞋子睡觉和头痛之间仅仅是关联性,没有因果性,它们之间有一个共同的原因:头天晚上喝酒。

穿鞋子睡觉的人和不穿鞋子睡觉的人有一个非常明显的不同:晚上是否喝酒。在平均喝酒人数这个feature上,两组的表现完全不同,所以这两个组之间完全没有可比性(除了是否穿鞋睡觉不同,晚上是否喝酒也有很大的不同)。当我们在做因果推断时,我们希望实验组与对照组除了treatment不一样以外,其他协变量的分布是完全一样的。
Confounding(混淆)是Treatment和Outcome的共同的原因(喝酒是穿鞋睡觉(Treatment)和头痛(Outcome)的共同的原因),从图上表示,在穿鞋睡觉和头痛之间有一个混杂关联,这就是我们观察到的现象。 这与因果关联不同,因果关联是指从穿鞋睡觉到头痛之间有一条单向边。通常情况下,我们观察到的关联是混杂关联和因果关联的混合。
虽然我们都知道相关不等于因果,但是在日常分析时,还是不可避免得陷入相关等于因果的误区。在头疼的这个例子里,我们可以用STAR来代替穿鞋子睡觉和睡前喝酒,这个STAR可以是任何闪入我们大脑里的念头。比如,某个人正好读了一个文章,上面说咖啡因会导致头痛,然后他恰好想起来了,他昨天喝了咖啡,他就会强化这个有偏见的认知“喝咖啡会导致头痛”,即便他很久以前读过另一篇文章“喝咖啡不会导致头痛”,但他几乎不会想起来这件事情。当我们头痛的时候就会想“我为什么会头痛,以后怎么做才不会头痛”。这就是一个常见的用相关代替因果的认知偏见的动机。比如,在我的认知里,我比较怀疑打疫苗的安全性,而打疫苗后正好有点头痛,我就会怀疑打疫苗引起了头痛;再比如,在我的认知里,小朋友多参加体育运动可以提升他的专注力,于是有时候我发现他的专注力有提升,就会归因到最近领他去参加的体育活动;

下图是真实的例子,绿线是5.21凌晨的完单量,蓝线是5.20日凌晨的完单量,红线是5.14凌晨的完单量,我们可以看到5.21凌晨2点多有一个小高峰,那么这是什么原因造成的呢?于是,各种各样与5.20,5.21相关的事件的信息会涌入我们的大脑:情人节?下雨?《速度与激情》上映?现实世界中会有很多这样用相关性代替因果性的例子,在真正进行因果推理时,需要大胆假设,小心论证。针对这个例子,那么我们如何使用其他更多信息来证明或者证伪我们刚才所做的各种假设呢?

这是另一个真实的数据,黑线是Nicolas的电影数量,红线是掉进泳池淹死的人的数量,这两份数据看起来在时间上有非常好的相关性。那我们会猜测下原因:1. Nicolas的电影会鼓动人们落水溺亡?2. Nicolas发现有人落水溺亡,于是他就拍电影劝说人们远离游泳池?3. 这俩原因都不是,这只是一种巧合?

所以,再重复一次,大家都听说了很多次的真理:关联不代表因果。在Brady的材料里,没有严格区分Correlation和Association,但在严格的定义中,这俩是不一样的。其中Association的含义最广,与“独立”/“不相关”相关。它表征的含义是 P ( X ∣ Y ) ! = P ( X ) P(X|Y)!=P(X) P(X∣Y)!=P(X), 也就是说在已知 Y Y Y的信息的情况下,我们对 X X X的认识是发生了变化的。而Correlation指的两个变量在趋势上有相关性。
那么,到底什么代表了因果关系的存在呢? 这个问题,对于研究因果推断的同学而言,我们必须要回答这个问题。我们如何知道一件事情是另外一件事情的因,且因果效应的大小如何衡量。
四、潜在结果
为了合理的推断因果效应,我们引入了一个新的概念:潜在结果。这个概念是因果推断所特有的,在常规的统计学或者机器学习的范畴里,用不着这个概念。假设在这个例子里,我们知道如果吃药,头痛会消失。而且同时我们也知道,如果不吃药,头痛就不会消失。如果这两件事情我们都知道,那我们就说这粒药丸对于头痛的治疗是有因果效应的。但是如果在另一个假设中,如果你没有吃药,头痛也消失了,也就是说,不论是否吃药,过一段时间头痛都消失了,那么在这种情况下,就说这粒药丸对于头痛的治疗没有因果效应。这是一个潜在结果的直观的例子。

现在,我们对潜在结果框架中的各种notation(符号)给出更形式化的定义: d o ( T = 1 ) do(T=1) do(T=1)表示服用了药丸; d o ( T = 0 ) do(T=0) do(T=0)表示不服药。在真实世界里,如果服药,那我们观察到的结果就是 Y i ∣ d o ( T = 1 ) Y_{i|do(T=1)} Yi∣do(T=1); 如果没有服药,那么观察到的结果就是 Y i ∣ d o ( T = 0 ) Y_{i|do(T=0)} Yi∣do(T=0); 对 d o do do操作进行简写后, Y i ( 1 ) Y_i(1) Yi(1)表示服药后的潜在结果, Y i ( 0 ) Y_i(0) Yi(0)表示服药前的潜在结果;于是我们定义这两者之间的差为Treatment T的因果效应。头痛后吃药的潜在结果之间的差异就是吃药的因果效应。
Y i ( 1 ) = 1 Y_i(1)=1 Yi(1)=1表示,如果吃药,头疼就好了; Y i ( 0 ) = 0 Y_i(0)=0 Yi(0)=0表示,如果不吃药,仍然头痛。但是,在潜在结果框架里有一个根本的问题:如果我们吃药了,就不会观察到不吃药会怎么样;如果我们没吃药,就不会观测到吃药会怎么样。在吃药时,我们称不吃药为反事实(counterfactual);在不吃药时,我们称吃药为反事实。反事实的缺失,是因果推断中的根本问题。所以我们单看个体,是没有办法测量其因果效应的,需要把个体放入群体中,才能够测量其因果效应。

4.1 ATE
Individual treatment effect是个体治疗效果,对于某一个特定的个体 i i i,它的因果效应是 I T E i = Y i ( 1 ) − Y i ( 0 ) ITE_i=Y_i(1)-Y_i(0) ITEi=Yi(1)−Yi(0) 。 由于我们观测不到个体治疗效果,所以很自然的,我们就会想到在群体中求平均,于是就引入了ATE的概念。但是不幸的是,潜在结果之间的差异与统计条件期望的差异不是一个概念。这是因为,关联不代表因果。在左下角的图里,因为T到Y之间除了蓝色的causal关联以外,还存在红色的混杂关联。潜在结果的差异等于causal association。但是条件期望的差是causal关联和混杂关联的混合。

4.2 RCT实验
也就是说,在有混杂存在时,我们不能通过观测到的条件期望的差异来进行因果效应的计算。如果有另外一种情况,没有从C到T的箭头,也就是说在另一个平行世界里,T不受C的影响,没有任何影响T的因素,那么就不存在混杂关联,就只有因果关联。这就是RCT实验所做的事情。RCT实验所做的事情就是把样本随机的分为治疗组或者对照组,样本到底属于治疗组还是对照组完全是随机的,比如抛硬币,比如使用随机数生成器。 在这种情况下,T没有任何因果图上的父亲结点。这时,对照组和治疗组是可比的。这也就是我们通常在做策略实验时,需要先判断实验组和对照组是否是AA调平的道理一致。
再回到前面那个穿鞋睡觉,早上起来头疼的例子里,问题在于穿鞋子睡觉的组与不穿鞋子睡觉的组是不可比的。两组人群在头天晚上喝酒的概率相差很大。如果我们能够随机控制一个人是否穿鞋子睡觉,然后做一个实验来看他早上起来是否头疼,那么我们就能够得到穿鞋子睡觉是否会导致头疼了。那么我们怎么做这个实验呢? 当每一个人要睡觉的时候,不论他是否醉酒,你先到他的房间里去抛一下硬币,如果硬币朝上,那么他穿鞋子睡觉,如果硬币朝下,那么他脱鞋子睡觉。这样做的结果就是,醉酒的人是均匀的分布在穿鞋子组和不穿鞋子组中的。
在上面的例子里, 随机使不同的组之间是可比的,这样就可以得到因果效应。在没有混杂时,平均因果效应就是条件期望的差。所以说,在能够做随机实验的场景下,因果推断相对容易。这也说明,一个好的随机实验对于因果推断非常重要。在这个相对简单的例子里,我们只有一个混杂变量C,对于那种有多个混杂变量的情况,甚至有未观测混杂变量的情况,如果有随机试验数据,那么就切断了任何混杂变量对治疗策略的影响。因为在随机实验数据中,T是由硬币决定的,不由其他任何变量决定。
我们在实际中如果能够碰到可以做随机实验的场景,也不要沾沾自喜,需要很小心的分析这个随机试验对于我们想要得到的结论是否真的随机,参加试验的样本是否能够代表策略真正实施的样本等等。
五、观测数据下的因果推断
下面我们讲讲观测数据下的因果推断。
理想情况下,我们做因果推断希望使用的数据如右上角,治疗策略不受任何其他变量控制,没有任何混杂,我们计算到的T对Y的影响就是因果效应。但是在实际情况中,我们会有各种各样的原因不能做随机控制实验。比如刚才脱鞋子睡觉的例子里,控制每一个参与实验的人配合实验是件非常有难度的事情;比如我们想要研究一个国家的意识形态(资本主义/共产主义)对GDP的影响, 这是不太可能的,因为我不认识任何一个人能够随机控制任何一个国家的意识形态;再比如研究一个人出生时的DNA对患癌症的影响,这也是绝对不可能的,因为在现在的科学技术体系下,我们还没有办法在一个人出生后对他的DNA作出修改。某些时候,做随机控制实验是不符合伦理道德的,比如想要研究吸烟对肺癌的影响,我们不可能控制一批人,通过抛硬币来决定谁吸烟谁不吸烟。在工业系统中,做随机控制实验是一件成本非常大的事情,它通常是以牺牲线上效率来收集数据的;某些时候,是不允许我们做随机控制实验的,比如节假日为了拉动TSH做的活动,我们想最大化业务收益,一般不会做随机控制实验;这样的例子还有很多……在这种情况下,我们就只能是在别人收集好的一个观测数据集上进行因果效应的研究。
那么问题来了,我们在观测数据下,如何度量因果效应呢? 接下来的内容将是本节课程中最不好理解的一部分,如果不能完全理解也没关系,我们在随后的课程中还会继续加强这方面的理解。
解决方法是对混杂变量进行调整/控制。在下面的式子里,使用W来表示混杂变量。如果 W W W是充分的调整/控制变量集合(所有的混杂都在 W W W中,不存在不在 W W W中的混杂变量),然后就有如下等式:在 W = w W=w W=w的子群体中,执行治疗 t t t的潜在结果 Y ( t ) Y(t) Y(t)就等于在条件 ( t , w ) (t,w) (t,w)下的期望。这里神奇的是,等式左边有 d o do do算子,等式右边没有 d o do do算子了。熟悉了各种统计方法的我们,自然更喜欢右边这种计算公式。这是为什么呢? 这是因为此处我们对 W W W进行控制,阻断了所有从T到Y的混杂路径,也就是右下角这张图中的阴影C被阻断,则我们计算到的T对Y的关联效应就是因果效应。但是这个因果效应是在W=w这个条件下计算的。如果我们只是想计算Y(t)的平均潜在因果效应,那只需要对W进行边缘化。

中间这张图显示了一种更复杂的情况。在这张图里,从T到Y有多个confounding path。 我们有多种方法来阻断这些混杂路径,比如我们可以同时控制 W 2 W_2 W2和 C C C;可以同时控制 W 1 W_1 W1和 C C C;控制了这些变量,等价于对T进行随机化。
对于右边这张图,有一个“V”字形的结构,这是一种对撞结构,其中 Z 2 Z_2 Z2被称为collider(对撞机)。 collider天然能够阻断混杂,所以在这种结构里我们不需要对任何变量进行控制。 相反的,如果我们对 Z 2 Z_2 Z2进行了控制,会打开 Z 1 Z_1 Z1到 Z 3 Z_3 Z3的通路,反倒引入了混杂。接下来的课程中会对这一块进行详细的介绍。这里可以介绍个简单的例子帮助大家理解对撞。 假设 Z 1 Z_1 Z1, Z 3 Z_3 Z3是两个独立变量, Z 2 = Z 1 + Z 3 Z_2=Z_1+Z_3 Z2=Z1+Z3, 当我们对 Z 2 Z_2 Z2进行控制时, Z 1 Z_1 Z1和 Z 3 Z_3 Z3就不再独立,于是就在 Z 1 Z_1 Z1和 Z 3 Z_3 Z3之间连接了一条混杂路径。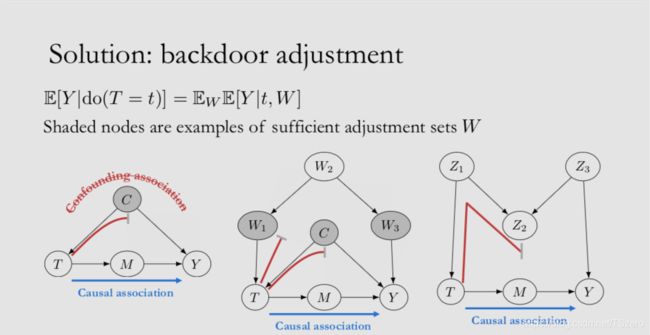
截止到现在,我们已经学习了如何使用调整公式来在观测数据上进行因果效应的计算,下面我们回到COVID-27这个数据集上来进行因果效应的计算。
在计算在整个数据集上的平均因果效应时,我们对C进行控制。,假设是在情况一的情景下,C是T的原因。所以我们对C进行边际化,而且因为C是离散变量,所以就等于在C的每个分组上对Y求期望,然后乘以c的概率。于是,我们增加了一列表示因果效应,在这个例子里,可以充分的看到治疗B是优于治疗A的。我们来一步一步深入这个公式进行计算,来跟条件期望进行对比。
首先,我们要计算 E [ Y ∣ t , c ] E[Y|t,c] E[Y∣t,c], 比如 E [ Y ∣ A , M i l d ] = 0.15 , E [ Y ∣ A , S e v e r e ] = 0.30 , E [ Y ∣ B , M i l d ] = 0.10 , E [ Y ∣ B , S e v e r e ] = 0.20 E[Y|A,Mild]=0.15, E[Y|A,Severe]=0.30, E[Y|B,Mild] = 0.10, E[Y|B, Severe] = 0.20 E[Y∣A,Mild]=0.15,E[Y∣A,Severe]=0.30,E[Y∣B,Mild]=0.10,E[Y∣B,Severe]=0.20. 也就是右下角的算式里的小括号里的数字。然后对c的边际概率进行计算,所以我们首先计算总人数 1400 + 100 + 50 + 500 = 2050. P ( M i l d ) = ( 1400 + 50 ) / 2050 , P ( S e v e r e ) = ( 100 + 500 ) / 2050 1400+100+50+500=2050. P(Mild) = (1400+50)/2050, P(Severe) = (100+500)/2050 1400+100+50+500=2050.P(Mild)=(1400+50)/2050,P(Severe)=(100+500)/2050. 不管对Treatment A还是Treatment B, P ( c ) P(c) P(c)都是一样的。我们把前后两种计算方法进行比较,就会发现我们使用了相同的 E [ Y ∣ t , c ] E[Y|t,c] E[Y∣t,c], 但是他们的权重不一样。在Causal的计算中,我们对Treatment A和Treatment B给了完全相同的weighting。当Condition是Treatment的原因时,采用上面的方法来计算因果效应就是错的。