机器学习之聚类算法Kmeans及其应用，调用sklearn中聚类算法以及手动实现Kmeans算法。

实现Kmeans算法实现聚类

要求：
1、根据算法流程，手动实现Kmeans算法；
2、调用sklearn中聚类算法，对给定数据集进行聚类分析；
3、对比上述2中Kmeans算法的聚类效果。

读取文件

def loadFile(path):
    dataList = []
    #打开文件：以二进制读模式、utf-8格式的编码方式                                                                                                打开
    fr = open(path,"r",encoding='UTF-8')
    record = fr.read()
    fr.close
    #按照行转换为一维表即包含各行作为元素的列表，分隔符有'\r', '\r\n', \n'
    recordList = record.splitlines()
    #逐行遍历：行内字段按'\t'分隔符分隔，转换为列表
    for line in recordList:
         if line.strip():
             dataList .append(list(map(float, line.split('\t'))))
    #返回转换后的矩阵
    recordmat = np.mat(dataList )
    return recordmat

手动实现Kmeans算法

def kMeans(dataset, k):
    m = np.shape(dataset)[0]
    ClustDist = np.mat(np.zeros((m, 2)))
    cents = randCents(dataset, k)
    clusterChanged = True
    # 循环迭代，得到最近的聚类中心
    while clusterChanged:
        clusterChanged = False
        for i in range(m):
            DistList = [distEclud(dataset[i, :], cents[jk,:]) for jk in range(k)]
            minDist = min(DistList)
            minIndex = DistList.index(minDist)

            if ClustDist[i, 0] != minIndex:
                clusterChanged = True
            ClustDist[i, :] = minIndex, minDist

        # 更新聚类
        for cent in range(k):
            ptsInClust = dataset[np.nonzero(ClustDist[:, 0].A == cent)[0]]
            # 更新聚类中心cents，axis=0按列求均值
            cents[cent, :] = np.mean(ptsInClust, axis=0)
    # 返回聚类中心和聚类分配矩阵
    return cents, ClustDist

处理数据

path_file = "TESTDATA.TXT"
recordMat = loadFile(path_file)
k = 4


cents, distMat = kMeans(recordMat, k)

绘制数据散点图

plt.subplot(311)
plt.grid(True)# 生成网格
for indx in range(len(distMat)):
    if distMat[indx, 0] == 0:
        plt.scatter(recordMat[indx, 0], recordMat[indx, 1], c='red', marker='o')
    if distMat[indx, 0] == 1:
        plt.scatter(recordMat[indx, 0], recordMat[indx, 1], c='blue', marker='o')
    if distMat[indx, 0] == 2:
        plt.scatter(recordMat[indx, 0], recordMat[indx, 1], c='cyan', marker='o')
    if distMat[indx, 0] == 3:
        plt.scatter(recordMat[indx, 0], recordMat[indx, 1], c='green', marker='o')

    #if distMat[indx, 0] == 4:
        #plt.scatter(recordMat[indx, 0], recordMat[indx, 1], c='black', marker='o')

绘制聚类中心

x = [cents[i,0] for i in range(k)]
y = [cents[i,1] for i in range(k)]
plt.scatter(x, y, s = 80, c='yellow', marker='o')
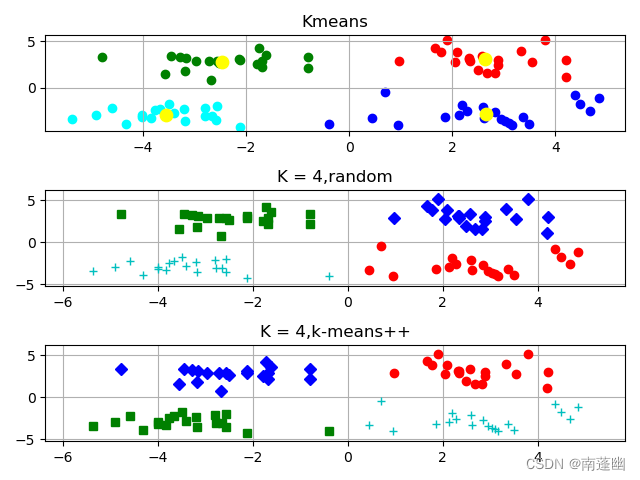
plt.title('Kmeans')

调用sklearn中聚类算法

from sklearn.cluster import KMeans
X = np.array(recordMat) # 生成初始聚类数据
#kmeans_model = KMeans(n_clusters=k, init='k-means++')  # 聚类模型
kmeans_model = KMeans(n_clusters=k, init='random')  # 聚类模型
kmeans_model.fit(X)  # 训练聚类模型

绘制k-Means聚类结果

# plt.figure()# 创建窗口
plt.subplot(312)
plt.axis([np.min(X[:,0])-1, np.max(X[:,0]+1), np.min(X[:,1])-1, np.max(X[:,1])+1])# 坐标轴
plt.grid(True)# 生成网格

colors = ['r', 'g', 'b','c'] # 聚类颜色
markers = ['o', 's', 'D', '+'] # 聚类标志
for i, l in enumerate(kmeans_model.labels_):
    plt.plot(X[i][0], X[i][1], color=colors[l],marker=markers[l],ls='None')
    plt.title('K = %s,random' %(k))

对比效果：

整合代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

def loadFile(path):
    dataList = []
    #打开文件：以二进制读模式、utf-8格式的编码方式                                                                                                打开
    fr = open(path,"r",encoding='UTF-8')
    record = fr.read()
    fr.close
    #按照行转换为一维表即包含各行作为元素的列表，分隔符有'\r', '\r\n', \n'
    recordList = record.splitlines()
    #逐行遍历：行内字段按'\t'分隔符分隔，转换为列表
    for line in recordList:
         if line.strip():
             dataList .append(list(map(float, line.split('\t'))))
    #返回转换后的矩阵
    recordmat = np.mat(dataList )
    return recordmat

def distEclud(vecA, vecB):
    return np.linalg.norm(vecA-vecB, ord=2)

def randCents(dataSet, k):
    n = np.shape(dataSet)[1]
    cents = np.mat(np.zeros((k,n)))
    for j in range(n):
        #质心必须在数据集范围内，也就是在min到max之间
        minCol = min(dataSet[:,j])
        maxCol = max(dataSet[:,j])
        #利用随机函数生成0到1.0之间的随机数
        cents [:,j] = np.mat(minCol + float(maxCol - minCol) * np.random.rand(k,1))
    return cents

def kMeans(dataset, k):
    m = np.shape(dataset)[0]
    ClustDist = np.mat(np.zeros((m, 2)))
    cents = randCents(dataset, k)
    clusterChanged = True
    # 循环迭代，得到最近的聚类中心
    while clusterChanged:
        clusterChanged = False
        for i in range(m):
            DistList = [distEclud(dataset[i, :], cents[jk,:]) for jk in range(k)]
            minDist = min(DistList)
            minIndex = DistList.index(minDist)

            if ClustDist[i, 0] != minIndex:
                clusterChanged = True
            ClustDist[i, :] = minIndex, minDist

        # 更新聚类
        for cent in range(k):
            ptsInClust = dataset[np.nonzero(ClustDist[:, 0].A == cent)[0]]
            # 更新聚类中心cents，axis=0按列求均值
            cents[cent, :] = np.mean(ptsInClust, axis=0)
    # 返回聚类中心和聚类分配矩阵
    return cents, ClustDist

path_file = "TESTDATA.TXT"
recordMat = loadFile(path_file)
k = 4


cents, distMat = kMeans(recordMat, k)
# 绘制数据散点图
plt.subplot(311)
plt.grid(True)# 生成网格
for indx in range(len(distMat)):
    if distMat[indx, 0] == 0:
        plt.scatter(recordMat[indx, 0], recordMat[indx, 1], c='red', marker='o')
    if distMat[indx, 0] == 1:
        plt.scatter(recordMat[indx, 0], recordMat[indx, 1], c='blue', marker='o')
    if distMat[indx, 0] == 2:
        plt.scatter(recordMat[indx, 0], recordMat[indx, 1], c='cyan', marker='o')
    if distMat[indx, 0] == 3:
        plt.scatter(recordMat[indx, 0], recordMat[indx, 1], c='green', marker='o')

    #if distMat[indx, 0] == 4:
        #plt.scatter(recordMat[indx, 0], recordMat[indx, 1], c='black', marker='o')

# 绘制聚类中心
x = [cents[i,0] for i in range(k)]
y = [cents[i,1] for i in range(k)]
plt.scatter(x, y, s = 80, c='yellow', marker='o')
plt.title('Kmeans')





X = np.array(recordMat) # 生成初始聚类数据
# plt.figure()# 创建窗口
plt.subplot(312)
plt.axis([np.min(X[:,0])-1, np.max(X[:,0]+1), np.min(X[:,1])-1, np.max(X[:,1])+1])# 坐标轴
plt.grid(True)# 生成网格

colors = ['r', 'g', 'b','c'] # 聚类颜色
markers = ['o', 's', 'D', '+'] # 聚类标志
#kmeans_model = KMeans(n_clusters=k, init='k-means++')  # 聚类模型
kmeans_model = KMeans(n_clusters=k, init='random')  # 聚类模型
kmeans_model.fit(X)  # 训练聚类模型
# 绘制k-Means聚类结果

for i, l in enumerate(kmeans_model.labels_):
    plt.plot(X[i][0], X[i][1], color=colors[l],marker=markers[l],ls='None')
    plt.title('K = %s,random' %(k))



X = np.array(recordMat) # 生成初始聚类数据
# plt.figure()# 创建窗口
plt.subplot(313)
plt.axis([np.min(X[:,0])-1, np.max(X[:,0]+1), np.min(X[:,1])-1, np.max(X[:,1])+1])# 坐标轴
plt.grid(True)# 生成网格

colors = ['r', 'g', 'b','c'] # 聚类颜色
markers = ['o', 's', 'D', '+'] # 聚类标志
kmeans_model = KMeans(n_clusters=k, init='k-means++')  # 聚类模型
# kmeans_model = KMeans(n_clusters=k, init='random')  # 聚类模型
kmeans_model.fit(X)  # 训练聚类模型
# 绘制k-Means聚类结果

for i, l in enumerate(kmeans_model.labels_):
    plt.plot(X[i][0], X[i][1], color=colors[l],marker=markers[l],ls='None')
    plt.title('K = %s,k-means++' %(k))

plt.show()