强化学习(1):马尔科夫决策过程
强化学习(1):马尔科夫决策过程
强化学习的基本原理:智能体在完成某项任务时,首先通过动作A与周围环境进行交互,在动作A和环境的作用下,智能体会产生新的状态,同时环境会给出一个立即回报。如此循环下去,智能体与环境不断交互从而产生很多数据。强化学习算法利用产生的数据修改自身的动作策略,再与环境进行交互,产生新的数据。并利用新的数据进一步改善自身的行为,经过数次迭代学习后,智能体最终学到完成相应任务的最优动作(最优策略)。

首先,我们来学习强化学习(1):马尔科夫的决策过程。内容如下:
- 马尔可夫性
- 马尔科夫过程
- 马尔科夫决策过程
- 贝尔曼方程
- 马尔科夫决策过程的伪代码
- 两种随机策略
马尔可夫性
马尔可夫性指的是系统的下一个状态St+1仅与当前状态St有关,而与以前的状态无关。
定义:状态St是马尔科夫的,当且仅当
![]()
定义中可以看出来,当前状态St其实是蕴含了所有相关的历史信息S1,S2…St,一旦当前状态已知,历史信息就会被抛弃。
马尔科夫过程
马尔科夫过程的定义:马尔科夫过程是一个二元组(S,P),且满足S是有限状态集合,P是状态转移矩阵。状态转移概率矩阵为:

如下图所示,一个学生的7种状态{娱乐,课程1,课程2,课程3,考过,睡觉,论文}:

每种状态的转换概率如下图所示。则该生从课程1开始一天可能的状态序列为:
课1-课2-课3-考过-睡觉
课1-课2-睡觉
以上状态序列称为马尔科夫链。当给定状态转移概率时,从某个状态出发存在多条马尔科夫链。对于游戏或者机器人,马尔科夫过程不足以描述其特点,因为不管游戏还是机器人,他们都是通过动作与环境进行交互,并从环境中获得奖励,而马尔科夫过程中不存在动作和奖励。将动作和回报考虑在内的马尔科夫过程称为马尔科夫决策过程。
马尔科夫决策过程
现在我们要对强化学习进行建模,这里利用马尔科夫决策过程进行建模,定义为(S,A,P,R,Υ):
S 为有限的状态集
A 为有限的动作集
P 为状态转移概率
R 为回报函数
Υ 为折扣因子,用来计算累积回报。
注意:跟马尔科夫过程不同的是,马尔科夫决策过程的状态转移概率是包含动作的,即:
![]()
强化学习的目标是给定一个马尔科夫决策过程,并寻找最优策略。所谓策略是指状态到动作的映射,策略常用符号π表示,它是指给定状态S时,动作集上的一个分布,即:

公式的含义:策略π在每个状态S指定的一个动作的概率。如果给出的策略π是确定的,那么策略π在每个状态S制定一个确定的动作。
(1)状态-值函数和状态-行为值函数
当智能体采用策略π时,累积回报服从一个分布,累计回报在状态S处的期望值定义为状态-值函数:
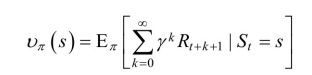
注意:状态值函数是与策略π相对应的,这是因为策略π决定了累积回报G的状态分布。
贝尔曼方程
用贝尔曼方程来推导状态-值函数和状态-行为值函数。
(1)状态-值函数的公式推导:

(2)状态-行为值函数:

(3)状态-值函数与状态-行为值函数的具体计算过程
其中,空心圆表示状态;实心圆表示状态-行为对。
状态-值函数的计算示意图如下:
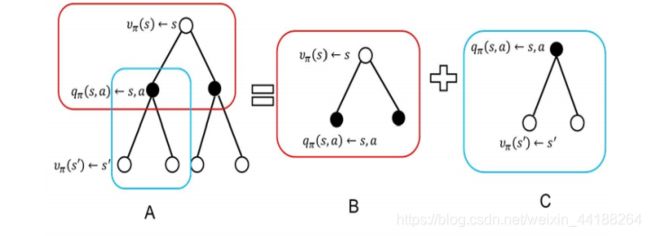
状态-值函数与状态-行为值函数的关系: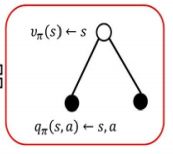

状态-值函数等于所有状态-行为值函数q的加权和。其中,π(a|s)状态下采取a行为的概率。下采取a行为的概率。
计算状态-行为值函数:
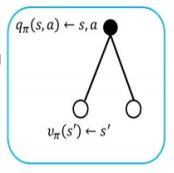
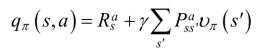
状态-行为值函数等于该状态、该行为执行后的即时奖励的期望值,加上它导致的所有下一步状态的折减后的状态-值函数V的加权和。
将上面两个图相加,就可以得到:
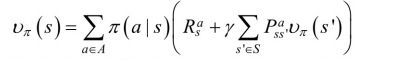
状态-行为值函数的计算示意图如下:

图B所示公式为:

两个图结合得到:

计算状态-值函数的目的是为了构建学习算法从学习中获取最优策略。每个策略都会对应一个状态值函数,最优策略自然对应着最优状态-值函数。
最优状态-值函数v(s):在所有策略中值最大的值函数,即:
![]()
最优状态-行为值函数q(s,a):在所有策略中最大的状态-行为值函数,即:
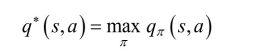
最优状态-值函数和最优状态-行为值函数的贝尔曼最优方程为:
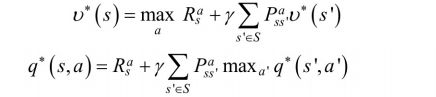
若已知最优状态-动作值函数,最优策略可通过最大化q*(s,a)来决定。
马尔科夫决策过程的伪代码
随机策略
最常用的概率分布也就是最常用的随机策略。
(1)贪婪策略
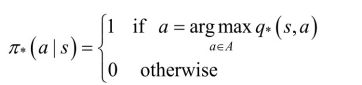
贪婪策略是一个确定性策略,即只有在使得动作值函数q*(s,a)最大的动作处取概率1,选其他动作的概率为0。
(2)ε-greedy策略
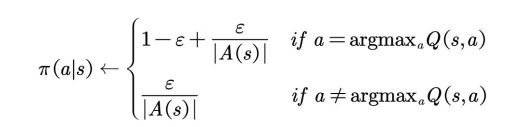
ε-greedy策略是强化学习最基本最常用随机策略。其含义是选取使得动作值函数最大的动作的概率为1-ε+ε/|A(s)|,而其他动作的概率为等概率,都为ε/|A(s)|。ε-greedy平衡了利用和探索,其中选取动作值函数最大的部分为利用,其他非最优动作仍有概率为探索部分。

