(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]
学习VLSI课程中广播结构FIR滤波器,利用折叠因子N=2将原有的8阶FIR滤波器通过折叠形成新的滤波器结构,分析其原理过程并且分析仿真。
一、8阶折叠结构的FIR滤波器
要求:
(1)列折叠方程计算折叠延迟
(2)画出折叠结构图
(3)编写8阶广播结构FIR滤波器程序并仿真
(4)编写折叠架构的8阶广播结构FIR滤波器程序并仿真,与普通8阶广播结构的FIR滤波器仿真结果进行比较,分析占用资源的情况。
首先让我们了解一下什么是广播结构,和平时正常的FIR滤波器用什么区别?
(广播)转置原理:SFG中所有边方向并且互换输入与输出端口,系统的功能保持不变,下图左图为转置前3阶FIR滤波器SFG图,右图为转置后,广播能够减少关键路径,从而使得结构功耗降低
转置前3阶FIR滤波器 SFG 转置后 3阶FIR滤波器 SFG
广播结构的3阶FIR滤波器
接下来进一步的了解什么是折叠?
折叠是通过减少功能单元、寄存器、多路选择器和互连线使得集成电路的柜面面积,通过将多个运算单元折叠为一个折叠集,在一个功能单元上执行多个算法运算,引入寄存器来存储信息,以时间换取面积。折叠技术在增加N倍时间的代价下,减少硬件功能单元数目可以到1/N,通过折叠变换,若是合理折叠集其中涉及折叠方程、架构图,若是不合理的折叠集,通过列折叠方程、重定时、约束图、重新构建滤波器结构,其中需要下列图2.1.1所示公式计算折叠方程。
图2.1.1 计算折叠方程过程
首先将FIR滤波器的运算单元进行编号,就按1-7编号即可。
依据下列公式列出折叠方程:
根据折叠方程绘制折叠结构图,见图2.1.2所示,可以看到其折叠结构图方程非常的有规律,依据折叠结构可以进行下一步的编写程序。
图2.1.2 8阶滤波器以折叠因子2折叠
程序编译结果:
RTL分析:
通过查看程序的RTL图,可以看到输入广播传到每个折叠集的乘法器,乘法器与每个加法器相连接,加法器与yout1相连接,并且在第一个延迟器和第三个延迟器与数据选择器相连接,其中利用CNT来控制数据选择器的选择,拉输入数据或者保留上次数据,并且通过CNT分别输入权重,由于CNT分俩种状态,于是可以将权重分为奇偶俩部分,.
程序代码分析:
程序中有重要几个部分,首先是SIGNAL信号线的定义,通过观察折叠的DFG图可以知道,其中每个折叠集的部分有三个延迟单元,有输入,有权重,输出,和滤波器的输出。
![]() 对于此部分,为寄存器部分,当上升沿到来便将数据存储到寄存器中,若不是上升沿便保持不变。
对于此部分,为寄存器部分,当上升沿到来便将数据存储到寄存器中,若不是上升沿便保持不变。
对于此部分为权重输入部分,CNT具有1和0俩个状态,由于是折叠因子为2,所以利用利用俩次将四个权重输入进去。
CNT类似于开关为0时,折叠集正常工作,数据按程序向前流动,当CNT为1时,数据经过三个延时单元重新返回折叠集,并且Y输出结果。
下列为四个乘法器的结果。可以知道Y1I是等于等于Y0O1。
依据公式当输入1时,并且语句程序可知,H0=80,当第一个上升沿来将第一个数据存入寄存器,待第二个上升沿来到的时候进行运算。
YOUT1=80*1=80; 第二个上升沿是输入1后续分析见代码部分即可了解。
二、8阶FIR滤波器(LMS自适应滤波器)
程序编译结果:
实验编译完成后查看程序的RTL图查看整题的电路结构,见图2图3.1 RTL图.1所示,这里可以清楚的看到其电路的结构和信号流向,其最前端相当于8阶的FIR滤波器。
图2.1 RTL图
对实验代码的介绍如下:
图2.2 右移实现第一次除2
如图2.2所示,该程序是将e的8到1位幅值给emu的7到0位,假设e的值为000001111,将其8到1位给emu7到0位后变为00000111,其值变为原来的1/2,也就是除了2,该程序实现了第一次除2。
图2.3 第二次除2
图2.4 第二次除2
图2.3和图2.4所示的代码实现的功能是第二次除2,与第一次除2合起来就是除了4,也就是1/4,因此可以得出步长因子的值为1/4;该代码的本质也是右移除2,图3-5的y取15到7位是为了去掉小数取整,将其幅值给sxty的8到0位,然后将其15到9位取最高位的值,也就是扩展位的意思,然后根据图3-4,将sxtd-sxty的值赋给e,之后根据图3-6 f(k)<=f(k)+xemu(k)(15 downto 8),就是将y的15到7位变成了15到8位,少了一位,也就相当于实现了右移,除了2。从而使步长因子的值为1/4。
三、俩滤波器比较
未折叠前广播结构的FIR滤波器见图4.3.1所示,以折叠因子为2进行折叠的广播结构FIR滤波器见图4.3.2所示。
在电路结果可以分析,折叠后寄存器数量增加,但是对于折叠因子N=2的折叠结果运算单元减半,运算时间减少,但是结构相对于普通的FIR滤波器来说较为复杂一些。
对于要深入比较还是需要深入研究并且加以区分
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第1张图片](http://img.e-com-net.com/image/info8/033e9ce5ac3e48058a5c68710941f814.jpg)
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第2张图片](http://img.e-com-net.com/image/info8/1549b8b64ed443538683292a0e3f8636.jpg)
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第3张图片](http://img.e-com-net.com/image/info8/a4c1618dd15e40a99e7b4b6f3f71b3da.jpg)
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第4张图片](http://img.e-com-net.com/image/info8/3190c2394c5e4b4680b6faa0a3acbac5.jpg)
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第5张图片](http://img.e-com-net.com/image/info8/c78a395277b64669acdaeee4daf9544c.jpg)
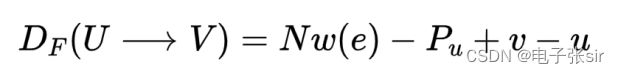
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第6张图片](http://img.e-com-net.com/image/info8/766323e59875424ea8be8756a94efefb.jpg)
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第7张图片](http://img.e-com-net.com/image/info8/23b737252dcc4264a99530b56e4f8724.jpg)
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第8张图片](http://img.e-com-net.com/image/info8/025acbe0fbf54ff0a864fbda9c8c95ec.jpg)
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第9张图片](http://img.e-com-net.com/image/info8/d81380c6a09343909d93b8030091d541.jpg)
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第10张图片](http://img.e-com-net.com/image/info8/c801fe7c2ecd44b9aabd5f875c9239de.jpg)
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第11张图片](http://img.e-com-net.com/image/info8/4d942f2d8f81467790b688db778e73b8.jpg)
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第12张图片](http://img.e-com-net.com/image/info8/6eb7695a9eb942b6a823751cf8e0a2d5.jpg)
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第13张图片](http://img.e-com-net.com/image/info8/54a9a0e96f184cba9e21d1735e4d8fc7.jpg)
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第14张图片](http://img.e-com-net.com/image/info8/08a9c853e4e34dd7933badb85d14833e.jpg)

![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第15张图片](http://img.e-com-net.com/image/info8/441e4e6311be4f5085e917ec75e7b8c2.jpg)
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第16张图片](http://img.e-com-net.com/image/info8/b33868a8a8eb494393a1ba9b41b128f0.jpg)

![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第17张图片](http://img.e-com-net.com/image/info8/fbd1b5ff677d41db8a09978e9f4a8a9e.jpg)
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第18张图片](http://img.e-com-net.com/image/info8/32ee439021104ee781f85fb2681ac4a2.jpg)
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第19张图片](http://img.e-com-net.com/image/info8/8e0adc66634e4f60ad9a978a9f5761a0.jpg)
![(LMS)8阶FIR滤波器以及8阶折叠结构FIR[VHDL]_第20张图片](http://img.e-com-net.com/image/info8/540afb04255846b0b1428e54ad4e9ae1.jpg)