时间序列作业
时间序列作业
作者:刘洋
学号:20210801068
邮箱:[email protected]
坐标:四川师范大学数学科学学院研究生院
作者介绍:一只被偏微分方程带偏了的人工智能算法设计师
文章目录
- (作业一)自协方差函数的Matlab实现
-
- 自协方差函数简介
- 上机实验报告
-
- 数据集
- 实验过程
-
- 洗发水销售数据集
- 股票信息数据集
- 参考文献
- (作业二)时间序列平稳化的 8 种方法比较及Matlab实现
-
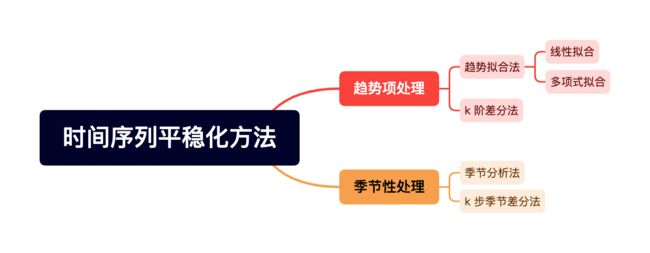
- 平稳化方法
- 趋势项处理
-
- 趋势拟合法
-
- 实验报告
- 程序源代码
- k 阶差分法
-
- 实验报告
- 程序源代码
- 季节性处理
-
- 季节分析法
-
- 实验报告
- 程序源代码
- k 步季节差分法
-
- 实验报告
- 程序源代码
- 时间序列平稳化的 8 种方法比较
-
- 趋势拟合+季节分析
- 趋势拟合+季节差分
- 差分法+季节分析
- 差分法+季节差分
- 小结
- 参考文献
- (汇报展示)AR 预测模型的 Matlab 实现
-
- 读取数据
- 原数据可视化
- 划分训练集和验证集
- 数据白噪声检验
- 数据平稳性检验
- 模型识别
-
- 自相关及偏自相关图像
- AIC & BIC 准则定阶
- 参数估计
- 残差的白噪声检验
- 预测
- 修正预测
- 参考文献
(作业一)自协方差函数的Matlab实现
自协方差函数简介
对于满足均值遍历性和二阶矩遍历性的平稳时间序列一次具体观测值 { x t , t = 1 , 2 , ⋯ , N } \left\{x_{t}, t=1,2, \cdots, N\right\} {xt,t=1,2,⋯,N}, 总体平均可转化为时间平均. 因此, 样本自协方差函数也通常可由下面两种方式计算得到:
{ γ ^ k = 1 N ∑ t = 1 N − k ( x t − μ ^ ) ( x t + k − μ ^ ) , 0 ⩽ k ⩽ N − 1 γ ^ k = γ ^ − k , 1 − N ⩽ k ⩽ − 1 , (1) \begin{cases}\hat{\gamma}_{k}=\frac{1}{N} \sum_{t=1}^{N-k}\left(x_{t}-\hat{\mu}\right)\left(x_{t+k}-\hat{\mu}\right), & 0 \leqslant k \leqslant N-1 \\ \hat{\gamma}_{k}=\hat{\gamma}_{-k}, & 1-N \leqslant k \leqslant-1,\end{cases}\tag{1} {γ^k=N1∑t=1N−k(xt−μ^)(xt+k−μ^),γ^k=γ^−k,0⩽k⩽N−11−N⩽k⩽−1,(1)
或
{ γ ^ k = 1 N − k ∑ t = 1 N − k ( x t − μ ^ ) ( x t + k − μ ^ ) , 0 ⩽ k ⩽ N − 1 γ ^ k = γ ^ − k , 1 − N ⩽ k ⩽ − 1 (2) \begin{cases}\hat{\gamma}_{k}=\frac{1}{N-k} \sum_{t=1}^{N-k}\left(x_{t}-\hat{\mu}\right)\left(x_{t+k}-\hat{\mu}\right), & 0 \leqslant k \leqslant N-1 \\ \hat{\gamma}_{k}=\hat{\gamma}_{-k}, & 1-N \leqslant k \leqslant-1\end{cases}\tag{2} {γ^k=N−k1∑t=1N−k(xt−μ^)(xt+k−μ^),γ^k=γ^−k,0⩽k⩽N−11−N⩽k⩽−1(2)
其中, μ ^ \hat{\mu} μ^ 为平稳序列的均值的估计值. 在实际应用中, 样本自协方差函数的计算通常采用第一种形式.
其原因在于, 利用 ( 1 ) (1) (1) 式定义的样本自协方差函数能使得 N N N 阶的样本自协方差矩阵
Γ ^ N = ( γ ^ k − j ) , k , j = 1 , 2 , ⋯ , N \hat{\boldsymbol{\Gamma}}_{N}=\left(\hat{\gamma}_{k-j}\right), k, j=1,2, \cdots, N Γ^N=(γ^k−j),k,j=1,2,⋯,N
正定.
为了计算自协方差矩阵(ACM),一种最直接的方式是利用两层循环嵌套结构计算,但此方式过于“原始”,对于长期序列计算速度相对比较慢.
注意到, 只要
y j = x j − μ ^ , j = 1 , 2 , ⋯ , N y_{j}=x_{j}-\hat{\mu}, \quad j=1,2, \cdots, N yj=xj−μ^,j=1,2,⋯,N
不全为零, 矩阵
A = ( 0 ⋯ 0 y 1 y 2 ⋯ y N − 1 y N 0 ⋯ y 1 y 2 y 3 ⋯ y N 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ y 1 ⋯ y N − 1 y N 0 ⋯ 0 0 ) N × ( 2 N − 1 ) \boldsymbol{A}=\left(\begin{array}{cccccccc} 0 & \cdots & 0 & y_{1} & y_{2} & \cdots & y_{N-1} & y_{N} \\ 0 & \cdots & y_{1} & y_{2} & y_{3} & \cdots & y_{N} & 0 \\ \vdots & & \vdots & \vdots & \vdots & & \vdots & \vdots \\ y_{1} & \cdots & y_{N-1} & y_{N} & 0 & \cdots & 0 & 0 \end{array}\right)_{N \times(2 N-1)} A=⎝⎜⎜⎜⎛00⋮y1⋯⋯⋯0y1⋮yN−1y1y2⋮yNy2y3⋮0⋯⋯⋯yN−1yN⋮0yN0⋮0⎠⎟⎟⎟⎞N×(2N−1)
是行满秩的. 样本自协方差矩阵可表示为
Γ ^ N = ( γ ^ 0 γ ^ 1 ⋯ γ ^ N − 1 γ ^ 1 γ ^ 0 ⋯ γ ^ N − 2 ⋮ ⋮ ⋮ γ ^ N − 1 γ ^ N − 2 ⋯ γ ^ 0 ) = 1 2 A A T \hat{\boldsymbol{\Gamma}}_{N}=\left(\begin{array}{cccc} \hat{\gamma}_{0} & \hat{\gamma}_{1} & \cdots & \hat{\gamma}_{N-1} \\ \hat{\gamma}_{1} & \hat{\gamma}_{0} & \cdots & \hat{\gamma}_{N-2} \\ \vdots & \vdots & & \vdots \\ \hat{\gamma}_{N-1} & \hat{\gamma}_{N-2} & \cdots & \hat{\gamma}_{0} \end{array}\right)=\frac{1}{2} \boldsymbol{A} \boldsymbol{A}^{\mathrm{T}} Γ^N=⎝⎜⎜⎜⎛γ^0γ^1⋮γ^N−1γ^1γ^0⋮γ^N−2⋯⋯⋯γ^N−1γ^N−2⋮γ^0⎠⎟⎟⎟⎞=21AAT
于是,得益于计算机对矩阵并行运算的优化.我们可以采用数组化编程思想,利用矩阵运算,轻松且快速的计算出自协方差矩阵.
上机实验报告
数据集
为了感受不同时间序列的统计性质,选用以下两种数据集分别建模.
- 洗发水销售数据集:
shampoo.csv - 上证指数数据集:
SH600031.csv
实验过程
洗发水销售数据集
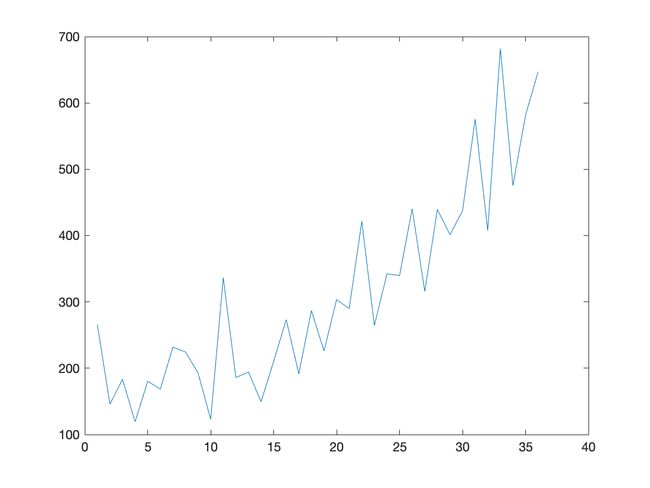
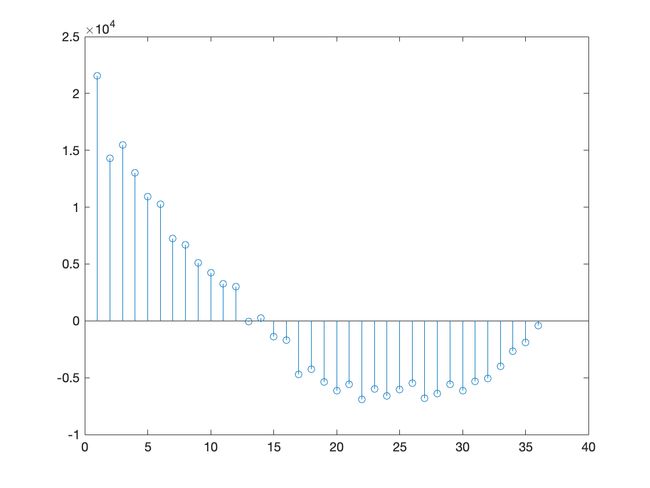
该数据集描述了每月洗发水的销售量
单位是销售计数,有36个观察值.
![]()
程序源代码
filename='shampoo.csv';
data = readmatrix(filename, 'OutputType', 'single');
x=data(1:36,2);
y=x-mean(x);
A=zeros(length(y),2*length(y)-1);
for i=1:length(y)
A(i,length(y)-i+1:length(y)-i+length(y))=y;
end
ACM=1/length(y).*A*A';
自协方差函数最大值:2.156610448813604e+04
自协方差函数最小值:-6.896521602231956e+03
从图像及数据可以发现:洗发水月销售量具有较明显的子相关性.
股票信息数据集
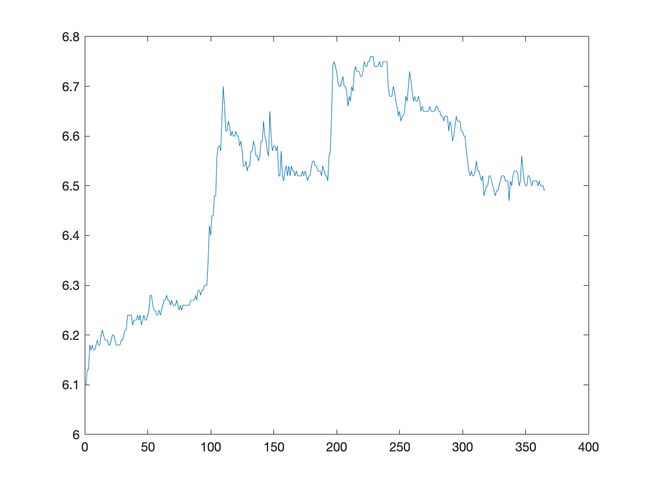
该数据集描述了上证指数每日的开盘,最高,最低,收盘,成交量,成交额.
取连续365天的开盘价进行建模.
程序源代码
filename='SH600031.csv';
data = readmatrix(filename, 'OutputType', 'single');
x=data(1:365,3);
y=x-mean(x);
A=zeros(length(y),2*length(y)-1);
for i=1:length(y)
A(i,length(y)-i+1:length(y)-i+length(y))=y;
end
ACM=1/length(y).*A*A';
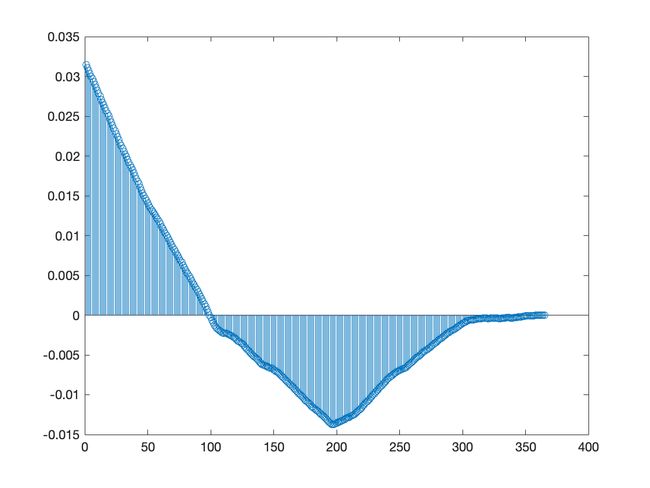
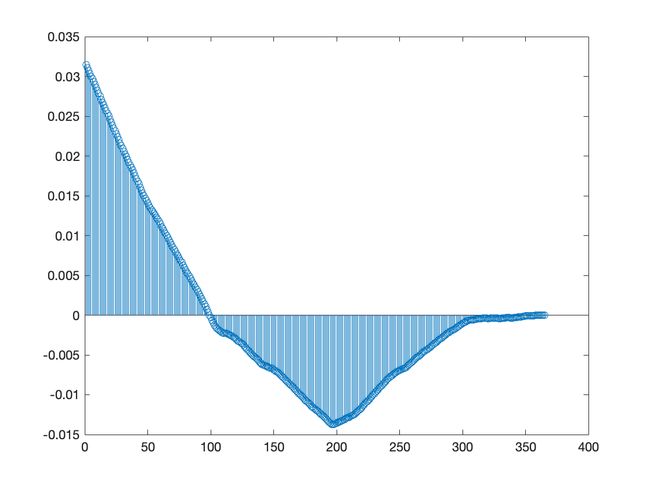
自协方差函数最大值:0.031476924974325
自协方差函数最小值:-0.013756630793134
从图像及数据可以发现:股市的开盘价没有明显的自相关性.
从时序图及自协方差函数图都能明显看出以上两个时间序列均为非平稳时间序列.
参考文献
周永道,王会琦,吕王勇.时间序列分析及应用.北京:高等教育出版社,2015.
数据集:
SH600031.csv
shampoo.csv
本人非统计专业,若有不妥之处, 恳请批评指正.
作者:图灵的猫
作者邮箱: [email protected]
(作业二)时间序列平稳化的 8 种方法比较及Matlab实现
时间序列模型建模流程图
平稳化方法
我们知道平稳序列具有许多良好的统计特性, 是传统时间序列分析的基础. 然而, 在自然界中和经济、工程等应用领域中, 我们所面对的时间序列通常具有非平稳性.
此时, 最自然的想法是通过一些简单的预处理方法将非平稳序列转化为平稳序列. 常用的有确定性分析和随机分析这两类平稳化方法. 在此主要介绍确定性分析方法.
为了能够更加清晰直观的理解时间序列平稳化方法,下面结合具体数据集编写程序,完成对非平稳序列的平稳化.
开发环境:
------------------------------------------------------------------------------------------------
MATLAB 版本: 9.12.0.1884302 (R2022a)
MATLAB 许可证编号: 968398
操作系统: macOS Version: 12.3 Build: 21E230
Java 版本: Java 1.8.0_202-b08 with Oracle Corporation Java HotSpot(TM) 64-Bit Server VM mixed mode
------------------------------------------------------------------------------------------------
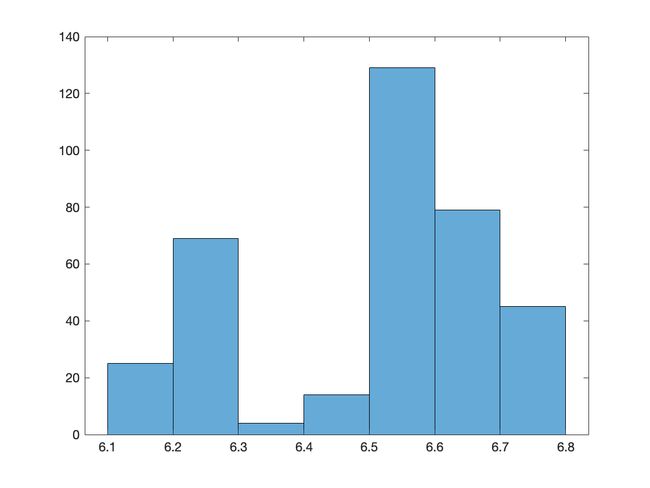
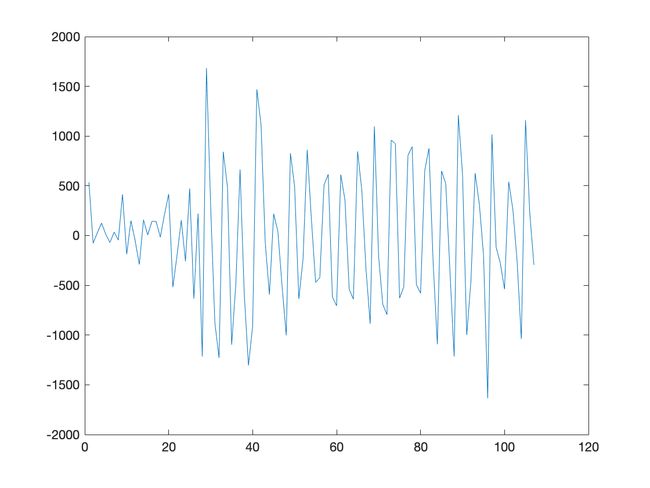
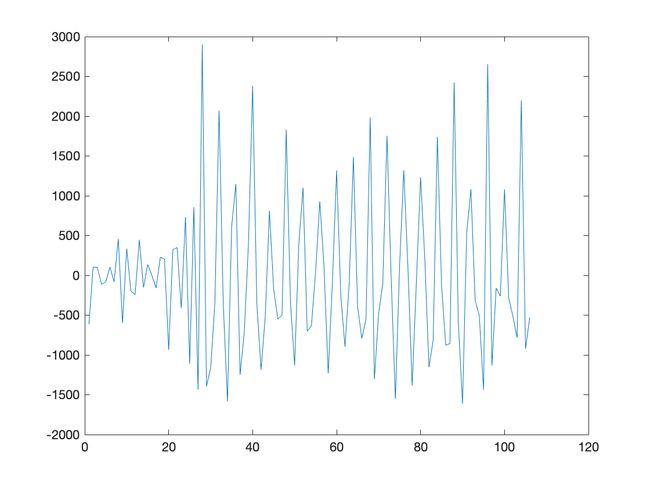
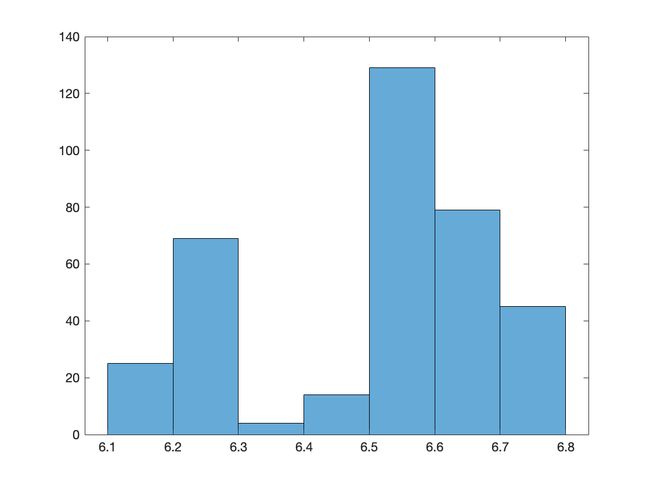
时间序列数据集:1965年3月至1994年3月澳大利亚毛纱季度产量
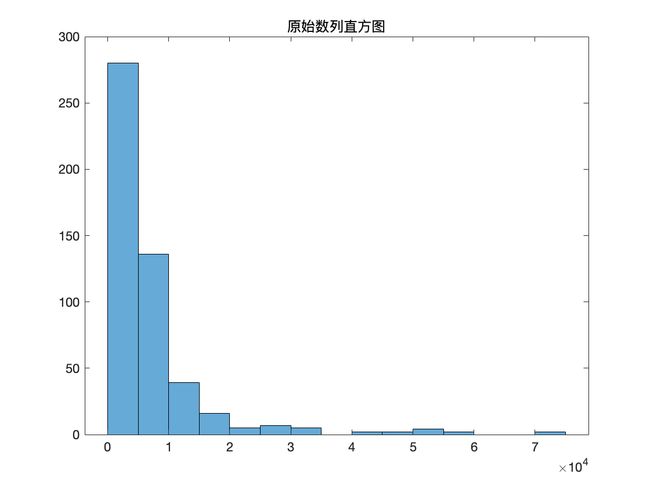
特点:具有趋势性和季节性、近似正态分布(柱状图),数据量108个
趋势项处理
经过长期的观察实践, 确定性分析法认为产生非平稳现象的确定性因素主要可以分解为两类
第一类: 长期趋势变动. 尽管时间序列一般呈现出随机起伏的形态, 但在一段较长时间内, 仍呈现递增、递减的转变形式. 这种大幅度变化通常是长期因素影响的结果, 如某地区年平均气温的变化, 我国人口总量的变化等都是长期因素所导致的, 它反映客观事物的主要变化趋势.
趋势拟合法
趋势拟合法就是把时间作为自变量, 相应的序列观测值作为因变量, 建立序列值随时间变化的回归模型. 为了便于理解, 这里暂时假设序列中不存在季节项, 即
X t = T t + R t E ( R t ) = 0 , Var ( R t ) = σ R 2 , (1) \begin{aligned} X_{t} &=T_{t}+R_{t} \\ E\left(R_{t}\right) &=0, \operatorname{Var}\left(R_{t}\right)=\sigma_{R}^{2}, \end{aligned}\tag{1} XtE(Rt)=Tt+Rt=0,Var(Rt)=σR2,(1)
其中,根据序列所表现出的线性或非线性性特征, 拟合法又有线性拟合和非 线性拟合, 对应假设 T t T_{t} Tt 为关于 t t t 的线性函数和非线性函数形式. ( 1 ) (1) (1) 式中 { R t } \left\{R_{t}\right\} {Rt} 的方差齐性是为保证趋势拟合中最小二乘参数估计的可靠性.
实验报告
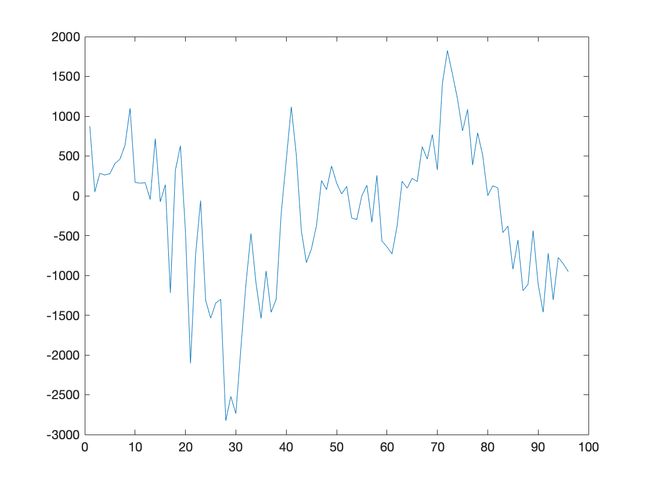
根据线性拟合处理后的时序图很容易发现,该处理对趋势项的消除并不理想,于是我们考虑使用高次多项式拟合来对趋势项进行处理.
可以发现,此时趋势项已被基本消除.
程序源代码
线性拟合函数:trend_fitting
function X_hat = trend_fitting(X)
% trend fitting 趋势拟合(线性) 去掉趋势项
% @X 原始时间序列
% @T 趋势项
% @X_hat 趋势拟合(线性) 去掉趋势项后时间序列
N=length(X);
t=1:N;
t_bar=sum(t)/N;
X_bar=sum(X)/N;
beta_1=(1/N*(t*X')-t_bar*X_bar)/(1/N*(t*t')-t_bar^2);
beta_0=X_bar-beta_1*t_bar;
T=beta_0+beta_1*t;
X_hat=X-T;
end
多项式拟合函数:polynomial_fitting
function X_hat = polynomial_fitting(X,n)
%Polynomial Fitting 趋势拟合(多项式) 去掉趋势项
% @n 拟合多项式次数 n
% @X 原始时间序列
% @beta n阶多项式的系数
% @T 趋势项
% @X_hat 趋势拟合(线性) 去掉趋势项后时间序列
N=length(X);
t=1:N;
beta = polyfit( t, X, n);
T=polyval(beta,t);
X_hat=X-T;
end
k 阶差分法
在许多实际问题中, 我们得到的观测数据序列显然不能近似看作是平稳的, 某些序列并不是稳定在同一水平上, 而是具有明显的增长或减少趋势. 例如某一地区的年平均温度所构成的时间序列 { x t } \left\{x_{t}\right\} {xt}, 短期内可能表现为上下起伏的随机变化, 但由于全球温室效应, 长期内总的温度变化趋势是增长的, 这显然是一个非平稳序列. 但若我们考察温度的增量 ∇ x t = x t − x t − 1 \nabla x_{t}=x_{t}-x_{t-1} ∇xt=xt−xt−1, 可将 { x t } \left\{x_{t}\right\} {xt} 的趋势消除, 转化为增量序列 { ∇ x t } \left\{\nabla x_{t}\right\} {∇xt} 在某一常值周围的平稳波动.
一般地, 对于非平稳序列 { X t } \left\{X_{t}\right\} {Xt}, 可以通过差分运算使之平稳化.通常对于蕴含着显著的线性趋势, 一阶差分就可以实现趋势平稳; 序列蕴含着曲线趋势, 二阶或三阶差分就可以提取曲线趋势的影响.
实验报告
编写 k 阶差分的函数
从时序图可以看出,使用 1 阶差分法处理后即可较好的消除趋势项.
意料之中, 2 阶差分法同样漂亮的完成了对趋势项的消除.
程序源代码
差分法函数:difference
function X_hat= difference(X,k)
%Difference 计算 k 阶差分
% @k k阶差分
% @X 原始时间序列
% @X_hat k 阶差分后时间序列
X_hat=X;
% X_hat=diff(X_hat,k) %可直接调用 k 阶差分
while k>0
X_hat=diff(X_hat);
k=k-1;
end
end
季节性处理
第二类: 季节性变化. 这类波动主要由本身就具有循环规律变化的影响因素所导致, 如季节规律性变化导致的月平均气温的循环波动, 每年节假日的规律性导致各类消费指数的循环波动等, 通常表现为长期趋势线上下的规律性周期波动. 有时也把循环波动和季节性变化分开考虑, 其实在实际分析时, 很难把固定周期的循环波动和季节性变化严格分解开, 因此此处中我们统一为季节性变化.
季节分析法
广义性的季节变动是指一种由于自然条件、消费习惯等因素的作用使研究对象呈现以一定时期为周期的较为规律性变化. 通常表现为一年内直接受自然季节的更替影响而发生的规律性增减变化, 如温度、降雨量等; 或是受间接影响而产生的规律性变化, 如价格消费指数、景点游客数等. 此外,一些受国家法定节假日和各地民俗民风等社会条件的影响, 工业生产、商品销售、交通运输等经营活动所具有的淡旺季周期性变动也属于广义季节变动的范畴.
季节分析法就是利用时间平均代替空间平均提取季节变动指数, 从而比较科学地对序列的发展作出预测.
实验报告
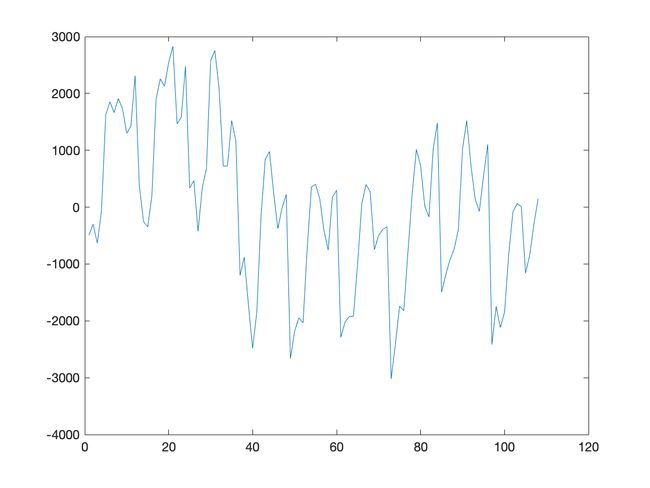
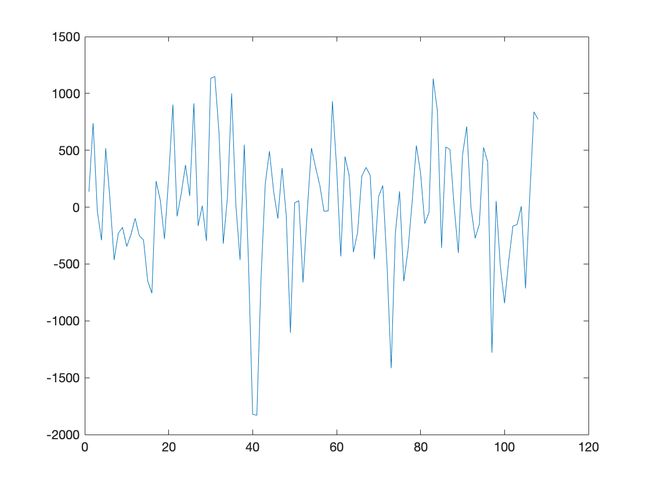
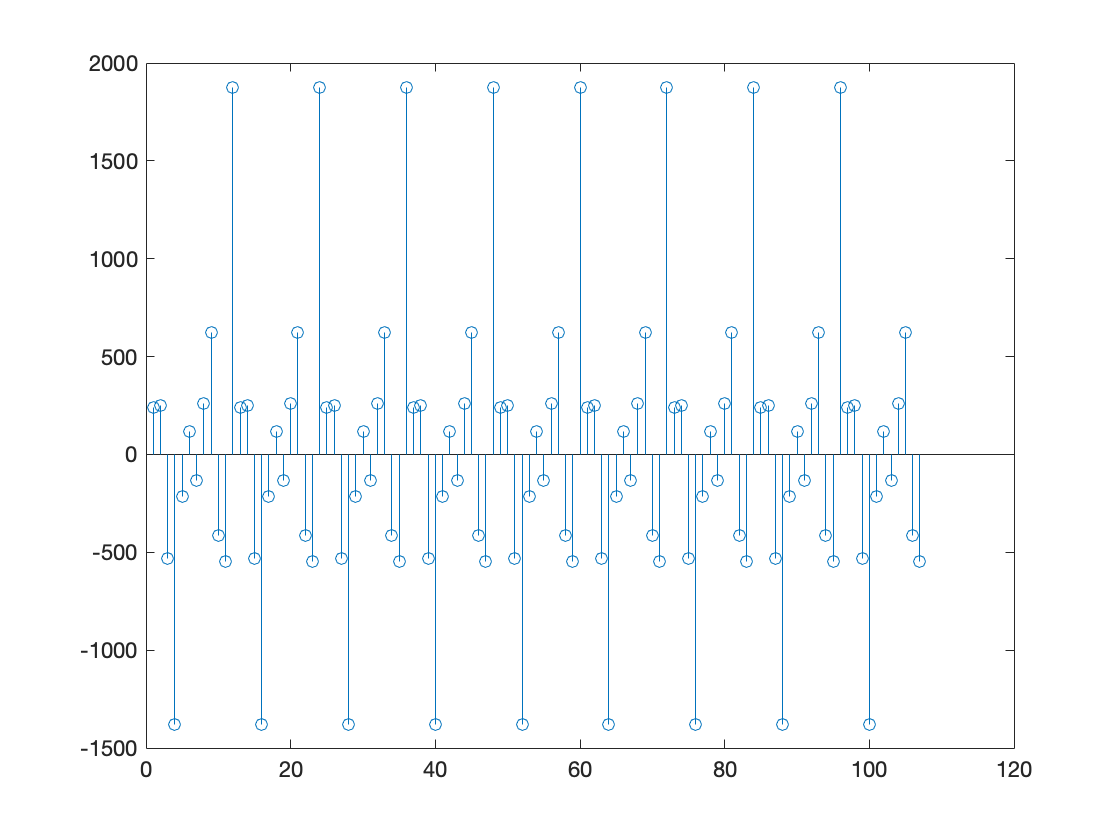
季节分析法需要仔细观察数据图来确认序列周期 m m m, 由于我们选取的时间序列数据集:1965年3月至1994年3月澳大利亚毛纱季度产量,具有趋势性和季节性,故选取周期为 12, 即 m = 12 m=12 m=12.
奇了个大怪,从时序图来看,隐隐约约感觉处理后季节性反而愈发明显了.
程序源代码
季节分析法函数:seasonal_analysis
function [X_hat,I]= seasonal_analysis(X,m)
%Seasonal Analysis 季节分析法去除周期性
% @m 季节周期
% @X 原始时间序列
% @S 趋势项
% @X_hat 季节分析法去除周期性后时间序列
% @I 季节指数
if mod(length(X),m)==0
n=length(X)/m;
X_jbar=zeros(m,1);
I=zeros(m,1);
S_0=zeros(m,1);
X_bar=1/(n*m)*sum(X);
for j=1:m
X_jbar(j)=1/n*sum(X((j-1)*n+1:(j-1)*n+n));
I(j)=X_jbar(j)/X_bar;
S_0(j)=X_bar*I(j);
end
S=repmat(S_0,n,1);
X_hat=X-S;
else
disp('使用季节分析法去除周期性时时间序列长度不能被周期整除');
disp('请修正后重新尝试喔,宝儿~');
end
end
k 步季节差分法
对于蕴含着固定周期的序列需进行步长为周期长度的差分运算, 称为季节差分法. 周期长度为 m m m 的季节差分算子常用 ∇ m = 1 − B m \nabla_{m}=1-\mathscr{B}^{m} ∇m=1−Bm 表示. 如果季节差分运算后为一平稳序列 { η t } \left\{\eta_{t}\right\} {ηt}, 则有
X t = X t − m + η t . X_{t}=X_{t-m}+\eta_{t} . Xt=Xt−m+ηt.
季节差分法的实质是使用延迟一个周期的历史数据作为自变量来刻画当期序列 值, 也是一种自回归方式提取确定性信息的方法.
实验报告
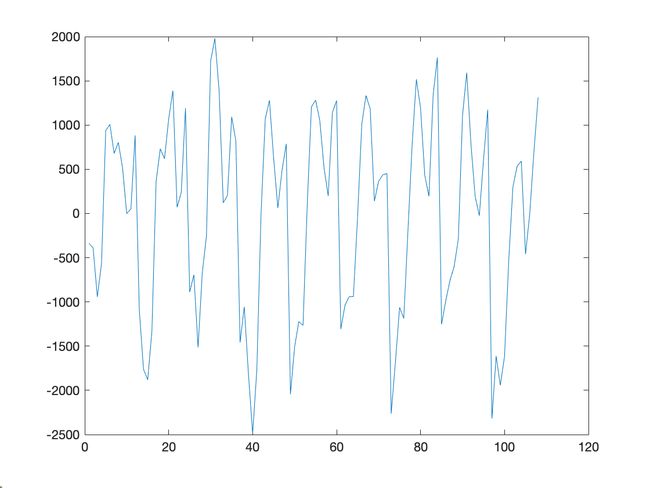
通过分析我们知道原始数据存在季节性,且周期为 12.
程序源代码
k 步季节差分法函数:seasonal_difference
function X_hat= seasonal_difference(X,k)
%seasonal difference 计算 k 步季节差分
% @k k步季节差分
% @X 原始时间序列
% @X_hat k 阶差分后时间序列
X_hat=zeros(length(X)-k,1);
for i=1:length(X)-k
X_hat(i)=X(i+k)-X(i);
end
end
时间序列平稳化的 8 种方法比较
对于一个存在趋势项和季节性的非平稳数据来说,根据思维导图可以轻松知道,我们选择不同的顺序和组合方式,可以得到 8 种排列的平稳化处理方法.
趋势拟合+季节分析
处理顺序:
- 趋势拟合
- 季节分析
实验报告
程序源代码
平稳化处理主程序:smooth
clc,clear
filename='data_woolyrnq.csv';
data = readmatrix(filename, 'OutputType', 'single');
x=data(1:108,1);
x_hat=x;
% 去除趋势(多项式拟合)
x_hat = polynomial_fitting(x_hat',4);
% 去周期(季节分析)
[x_hat,I]= seasonal_analysis(x_hat,12);
处理顺序:
- 季节分析
- 趋势拟合
实验报告
程序源代码
平稳化处理主程序:smooth
clc,clear
filename='data_woolyrnq.csv';
data = readmatrix(filename, 'OutputType', 'single');
x=data(1:108,1);
x_hat=x;
% 去周期(季节分析)
[x_hat,I]= seasonal_analysis(x_hat,12);
% 去除趋势(多项式拟合)
x_hat = polynomial_fitting(x_hat',4);
趋势拟合+季节差分
处理顺序:
- 趋势拟合
- 季节差分
实验报告
程序源代码
平稳化处理主程序:smooth
clc,clear
filename='data_woolyrnq.csv';
data = readmatrix(filename, 'OutputType', 'single');
x=data(1:108,1);
x_hat=x;
% 去除趋势(多项式拟合)
x_hat = polynomial_fitting(x_hat',4);
% 去周期(k 步季节差分)
x_hat= seasonal_difference(x_hat,12);
处理顺序:
- 季节差分
- 趋势拟合
实验报告
程序源代码
平稳化处理主程序:smooth
clc,clear
filename='data_woolyrnq.csv';
data = readmatrix(filename, 'OutputType', 'single');
x=data(1:108,1);
x_hat=x;
% 去周期(k 步季节差分)
x_hat= seasonal_difference(x_hat,12);
% 去除趋势(多项式拟合)
x_hat = polynomial_fitting(x_hat',4);
差分法+季节分析
处理顺序:
- 差分法
- 季节分析
实验报告
程序源代码
平稳化处理主程序:smooth
clc,clear
filename='data_woolyrnq.csv';
data = readmatrix(filename, 'OutputType', 'single');
x=data(1:108,1);
x_hat=x;
% 去除趋势(k 阶差分)
x_hat_1= difference(x,1);
x_hat_1=[x_hat_1;0];
% 去周期(季节分析)
[x_hat_1,I]= seasonal_analysis(x_hat_1,12);
x_hat_1=x_hat_1(1:end-1);
由于作差分后序列长度会变化,故需作补齐处理.
处理顺序:
- 季节分析
- 差分法
实验报告
程序源代码
平稳化处理主程序:smooth
clc,clear
filename='data_woolyrnq.csv';
data = readmatrix(filename, 'OutputType', 'single');
x=data(1:108,1);
x_hat=x;
% 去周期(季节分析)
[x_hat,I]= seasonal_analysis(x_hat,12);
% 去除趋势(k 阶差分)
x_hat= difference(x_hat,1);
差分法+季节差分
处理顺序:
- 差分法
- 季节差分
实验报告
程序源代码
平稳化处理主程序:smooth
clc,clear
filename='data_woolyrnq.csv';
data = readmatrix(filename, 'OutputType', 'single');
x=data(1:108,1);
x_hat=x;
% 去除趋势(k 阶差分)
x_hat_1= difference(x,1);
x_hat_1=[x_hat_1;0];
% 去周期(季节差分)
[x_hat_1,I]= seasonal_analysis(x_hat_1,12);
x_hat_1=x_hat_1(1:end-1);
由于作差分后序列长度会变化,故需作补齐处理.
处理顺序:
- 季节差分
- 差分法
实验报告
处理结果图:
程序源代码
平稳化处理主程序:smooth
clc,clear
filename='data_woolyrnq.csv';
data = readmatrix(filename, 'OutputType', 'single');
x=data(1:108,1);
x_hat=x;
% 去周期(季节差分)
[x_hat,I]= seasonal_analysis(x_hat,12);
% 去除趋势(k 阶差分)
x_hat= difference(x_hat,1);
季节差分、差分法不同处理顺序的差别
小结
为了能够更加清晰直观的理解时间序列平稳化方法,我们结合具体数据集编写Matlab程序,完成对非平稳序列的平稳化.
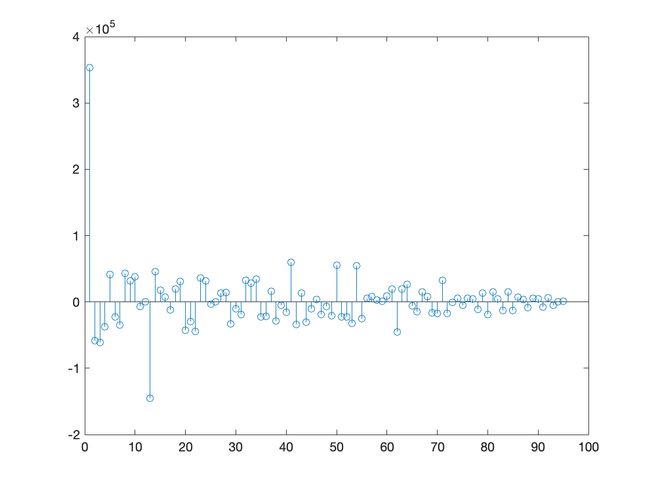
通过对时间序列平稳化的 8 种方法比较及Matlab实现,从逐点曼哈顿距离图可以发现,除了季节性差分配合差分法平稳化外,其余几种组合方式的处理结果均与操作顺序有关.
参考文献
周永道,王会琦,吕王勇.时间序列分析及应用.北京:高等教育出版社,2015.
数据集:
SH600031.csv
data_woolyrnq.csv
shampoo.csv
本人非统计专业,若有不妥之处, 恳请批评指正.
作者:图灵的猫
作者邮箱: [email protected]
(汇报展示)AR 预测模型的 Matlab 实现
时间序列模型建模流程图
读取数据
上证指数数据集:SH600031.csv
该数据集描述了三一重工 2017 年每日的开盘、最高、最低、收盘、成交量、成交额.
下面取连续500次成交量的观测数据进行建立时间序列模型并预测.
前 10 行数据预览
"2017/01/03" "09:35" "6.10" "6.14" "6.10" "6.13" "2851.00" "1745600.00"
"2017/01/03" "09:40" "6.13" "6.13" "6.11" "6.13" "1413.00" "865200.00"
"2017/01/03" "09:45" "6.13" "6.18" "6.12" "6.18" "5662.00" "3487800.00"
"2017/01/03" "09:50" "6.18" "6.19" "6.17" "6.18" "4891.00" "3022800.00"
"2017/01/03" "09:55" "6.17" "6.18" "6.17" "6.18" "3300.00" "2038900.00"
"2017/01/03" "10:00" "6.18" "6.18" "6.17" "6.17" "2649.00" "1635400.00"
"2017/01/03" "10:05" "6.17" "6.18" "6.16" "6.16" "3107.00" "1917000.00"
"2017/01/03" "10:10" "6.17" "6.18" "6.16" "6.18" "5671.00" "3499300.00"
"2017/01/03" "10:15" "6.18" "6.19" "6.17" "6.18" "6490.00" "4011200.00"
"2017/01/03" "10:20" "6.19" "6.19" "6.17" "6.17" "3041.00" "1877400.00"
程序源代码
clc,clear
%% 读取数据
filename='SH600031.csv';
Data = readmatrix(filename, 'OutputType', 'string');
data = str2double(Data(1:500,7));
N = length(data);
原数据可视化
程序源代码
%% 原数据可视化
figure(1)
plot(data);
title('三一重工股票成交量时序图')
ylabel('成交量')
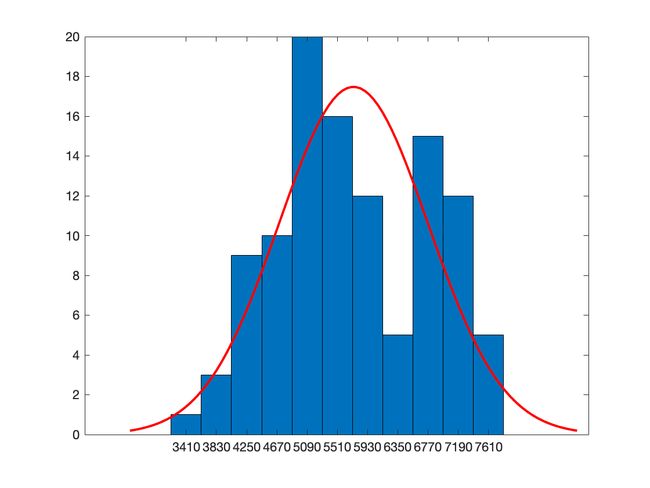
figure(2)
histogram(data);
title('原始数列直方图')
划分训练集和验证集
因为要对数据进行预测,所以我们将数据分为 70% 的训练集及 30% 的测试集.
程序源代码
%% 划分训练集和测试集
trg = round(0.7*N);
TrainData = data(1:trg);
TestData = data(trg+1:end);
数据白噪声检验
程序源代码
%% 数据白噪声检验
disp('数据白噪声检验')
[hLBQ,pLBQ] = lbqtest(TrainData);
disp('检验结果如下')
hLBQ,pLBQ
命令行窗口输出
数据白噪声检验
检验结果如下
hLBQ =
logical
1
pLBQ =
0
输出变量说明:
hLBQ 表示测试的结果
hLBQ = 1 表示拒绝数据无自相关的零假设而选择备择假设.(非白噪声序列)
hLBQ = 0 表示接受数据无自相关的零假设.(白噪声序列)
pLBQ 表示 lb 检验统计量的概率 p 值.
数据平稳性检验
程序源代码
%% 数据平稳性检验
disp('使用 PP 检验, 如果不能拒绝原假设, 则说明序列存在单位根')
[hp,hpValue,stat,cValue,reg] = pptest(TrainData,'model','Ts');
disp('检验结果如下:')
hp,hpValue
diff = 0;
while hp == 0
disp('hp=0,说明原始序列不平稳')
disp('对序列作差分处理,再对差分数据进行 PP 检验,检验结果如下:')
smooth_data = diff(TrainData);
% % 去除趋势(线性拟合)
% smooth_data=trend_fitting(smooth_data');
% % 去除趋势(多项式拟合)
% smooth_data = polynomial_fitting(smooth_data',4);
% % 去周期(季节分析)
% [smooth_data,I]= seasonal_analysis(smooth_data',12);
% % 去除趋势(k 阶差分)
% smooth_data= difference(smooth_data,1);
% % 去周期(k 步季节差分)
smooth_data= seasonal_difference(smooth_data,12);
[hp,hpValue,stat,cValue,reg] = pptest(smooth_data,'model','Ts');
hp,hpValue
diff = diff + 1;
end
disp('hp=1,原始序列平稳')
smooth_data = TrainData;
命令行窗口输出
使用 PP 检验, 如果不能拒绝原假设, 则说明序列存在单位根
检验结果如下:
hp =
logical
1
hpValue =
1.0000e-03
hp=1,原始序列平稳
模型识别
自相关及偏自相关图像
程序源代码
%% 自相关及偏自相关图像
%原序列图片
figure(3)
subplot(2,1,1)
autocorr(TrainData);
title('成交量的自相关图像')
subplot(2,1,2)
parcorr(TrainData)
title('成交量的偏自相关图像')
if diff >=1
% 平滑化后图片
figure(4)
subplot(2,1,1)
autocorr(smooth_data);
title('平稳化后的自相关图像')
subplot(2,1,2)
parcorr(smooth_data)
title('平稳化后的偏自相关图像')
end
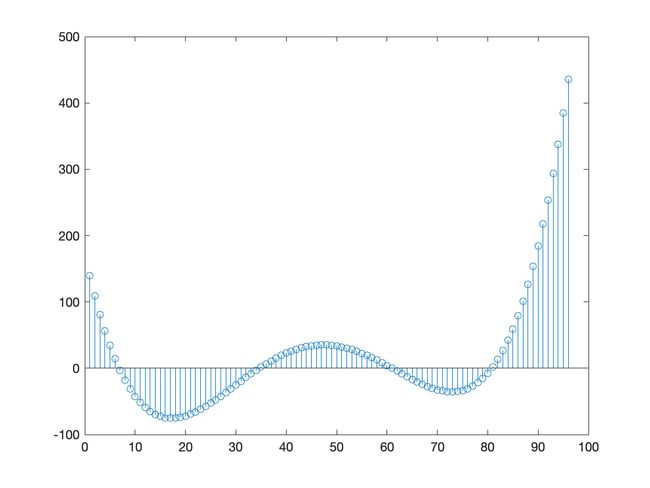
从自相关及偏自相关图像可以看出, 自相关系数缓慢衰减,可以判定自相关系数拖尾,而偏自相关系数在延迟 2 阶后都在2 倍标准差范围里面. 可以认为 2 阶后偏自相关系数为零, 所以偏自相关系数 2 阶后截尾, 由 AR 模型的统计特性,可以初步判定该数据是 AR(2) 模型.
AIC & BIC 准则定阶
在对 AR 模型识别时, 根据其样本偏自相关系数的截尾步数, 可初步得到 A R \mathrm{AR} AR 模型的阶数 p p p. 然而, 此时建立的 AR ( p ) \operatorname{AR}(p) AR(p) 模型末必是最优的. 一个好模型通常要求残差序列方差较小, 同时模型也相对简单, 即要求阶数较低. 因此, 我们需要一些准则来比较不同阶数的模型之间的优劣, 从而确定最合适的阶数.
- Akaike 信息准则
Akaike 信息准则, 简称为 AIC 准则, 是一种基于观测数据选择最优参数模型的信息准则, 它既要衡量模型对原始数据的拟合程度, 又要考虑模型中所含待估参数的个数, 即模型的复杂程度.
定义 AIC 信息准则如下:
AIC ( p ) = ln σ ^ 2 + 2 ( p + 1 ) N , \operatorname{AIC}(p)=\ln \hat{\sigma}^{2}+\frac{2(p+1)}{N}, AIC(p)=lnσ^2+N2(p+1),
其中 p + 1 p+1 p+1 为待估参数个数, 即 AR ( p ) \operatorname{AR}(p) AR(p) 模型的 p p p 个自回归系数 a 1 , ⋯ , a p a_{1}, \cdots, a_{p} a1,⋯,ap 以及随机误差的方差 σ 2 \sigma^{2} σ2.
程序源代码
%% AIC 准则定阶
maxLags = 8;
AIC = zeros(maxLags,1);
for j=1:maxLags
mdl = ar(smooth_data,j);
AIC(j) = mdl.Report.Fit.AIC;
end
% 画热度图来表示 AIC 数值的分布
figure(4)
heatmap(AIC/1000);
xlabel("AIC")
ylabel("AR Lags")
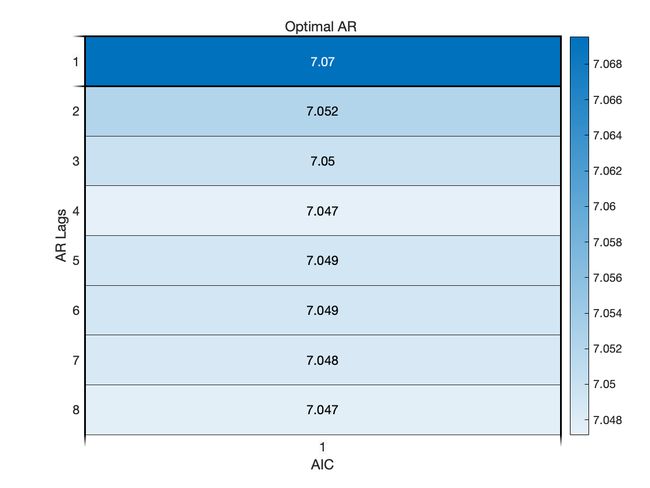
OptimalARLags_AIC = find(AIC==min(AIC));
title('Optimal AR ')
AIC 准则下的最优 AR 模型的阶数为 4 阶.
- BIC 准则
模拟研究结果表明, 当观测序列长度 N N N 较大时, AIC 准则有使 p p p 值估计 过高的倾向. 通过修正拟合残差方差和拟合模型参数个数之间的权重, 得到贝叶斯信息准则, 简称为 BIC 准则, 其定义如下:
B I C ( p ) = ln σ ^ 2 + ln N ( p + 1 ) N . \mathrm{BIC}(p)=\ln \hat{\sigma}^{2}+\frac{\ln N(p+1)}{N} . BIC(p)=lnσ^2+NlnN(p+1).
A I C \mathrm{AIC} AIC 准则与 BIC 准则的差异仅在于将 A I C \mathrm{AIC} AIC 中后一项中的 2 换为 ln N \ln N lnN, 而这一项表示模型阶数 p p p 对 AIC 和 BIC 取值大小的作用, 2 和 ln N \ln N lnN 相当于对 p p p 的加权系数. 当 N N N 较大时, 有 ln N ≫ 2 \ln N \gg 2 lnN≫2, 因此在 BIC 准则中模型阶数 p p p 的 增加对 BIC 值的影响较大, 所以 BIC 准则确定的实用模型的阶数将低于 AIC 准则确定的阶数. 可以证明, BIC 准则确定的模型阶数是其真值的一致估计.
事实上, 定义不同的准则函数, 是为了对拟合残差与参数个数之间进行不同的权衡, 以体现使用者在模型拟合误差与模型复杂程度之间的不同侧重.
程序源代码
%% BIC 准则定阶
maxLags = 8;
BIC = zeros(maxLags,1);
for j=1:maxLags
mdl = ar(smooth_data,j);
BIC(j) = mdl.Report.Fit.BIC;
end
% 画热度图来表示 BIC 数值的分布
figure(5)
heatmap(BIC/1000);
xlabel("BIC")
ylabel("AR Lags")
OptimalARLags_BIC = find(BIC==min(BIC));
title('Optimal AR ')
BIC 准则下的最优 AR 模型的阶数为 2 阶.
参数估计
通过以上分析可知, BIC 准则下的最优 AR 模型的阶数为 2 阶. 于是考虑建立 AR(2) 模型.
程序源代码
%% 参数估计
disp("建立的 AR 模型如下")
mdl = ar(smooth_data,OptimalARLags_BIC)
a = zeros(length(mdl.Report.Parameters.ParVector),1);
a(1:length(mdl.Report.Parameters.ParVector)) = -mdl.Report.Parameters.ParVector;
命令行窗口输出
建立的 AR 模型如下
mdl =
Discrete-time AR model: A(z)y(t) = e(t)
A(z) = 1 - 0.6436 z^-1 - 0.2325 z^-2
采样时间: 1 seconds
Parameterization:
Polynomial orders: na=2
Number of free coefficients: 2
Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using AR ('fb/now') on time domain data "smooth_data".
Fit to estimation data: 30.82%
FPE: 3.296e+07, MSE: 3.259e+07
残差的白噪声检验
程序源代码
%% 残差的白噪声检验
epsilon = zeros(length(TrainData)-OptimalARLags_BIC,1);
x_hat = zeros(length(TrainData)-OptimalARLags_BIC,1);
for j =OptimalARLags_BIC+1:length(TrainData)
x_hat(j) = smooth_data(j-OptimalARLags_BIC:j-1)'*flipud(a(1:length(mdl.Report.Parameters.ParVector)));
epsilon(j) = smooth_data(j) - x_hat(j);
end
var_epsilon = var(epsilon);
mean_epsilon=mean(epsilon);
figure(6)
subplot(1,2,1)
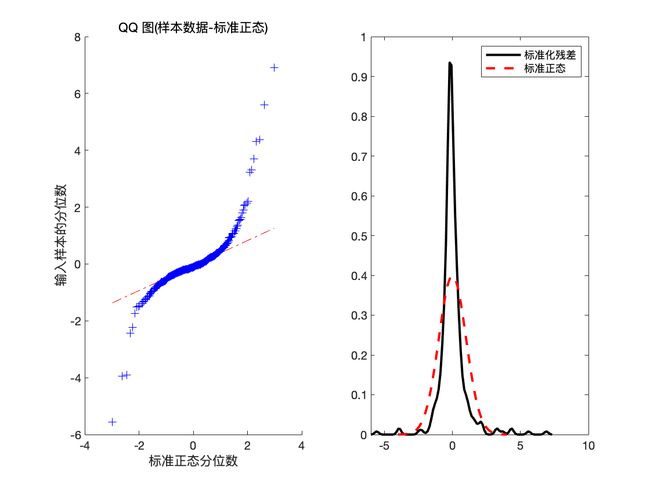
qqplot((epsilon-mean_epsilon)/sqrt(var_epsilon))
x = -4:.05:4;
[f,xi] = ksdensity((epsilon-mean_epsilon)/sqrt(var_epsilon));
subplot(1,2,2)
plot(xi,f,'k','LineWidth',2);
hold on
plot(x,normpdf(x),'r--','LineWidth',2);
legend('标准化残差','标准正态')
hold off
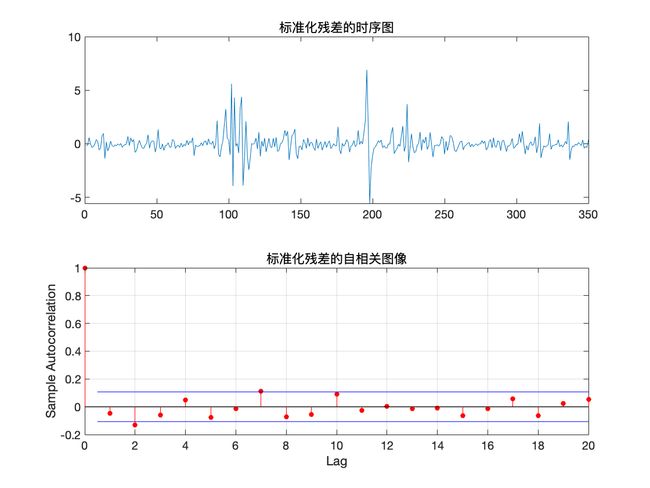
figure(7)
subplot(2,1,1)
plot((epsilon-mean_epsilon)/sqrt(var_epsilon));
title('标准化残差的时序图')
subplot(2,1,2)
autocorr((epsilon-mean_epsilon)/sqrt(var_epsilon))
title('标准化残差的自相关图像')
disp('检查残差是否存在相关性')
[hLBQ,pLBQ] = lbqtest(epsilon);
disp('检验结果如下')
hLBQ,pLBQ
命令行窗口输出
检查残差是否存在相关性
检验结果如下
hLBQ =
logical
0
pLBQ =
0.1111
输出变量说明
hLBQ 表示测试的结果
hLBQ = 1 表示拒绝数据无自相关的零假设而选择备择假设.(非白噪声序列)
hLBQ = 0 表示接受数据无自相关的零假设.(白噪声序列)
pLBQ 表示 lb 检验统计量的概率 p 值.
可以看到此时 hLBQ = 0, 于是可判定残差不具有相关性, 因此模型可以信任.
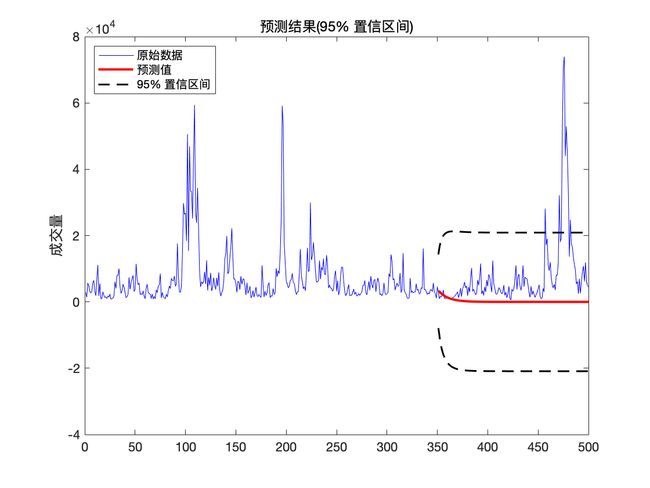
预测
我们利用建好的模型进行最佳线性预测,预测训练集后的数据,并画出预测数据的 95 % 95\% 95% 置信区间.
X t + k X_{t+k} Xt+k 的最佳线性预测可表示为
X ^ t ( k ) = L ( X t + k ∣ X t ) = { ∑ j = 1 p a j X t + 1 − j k = 1 ∑ j = 1 k − 1 a j X ^ t ( k − j ) + ∑ j = k p a j X t + k − j , 1 < k ⩽ p ∑ j = 1 p a j X ^ t ( k − j ) , k > p \begin{aligned} \hat{X}_{t}(k) &=L\left(X_{t+k} \mid \boldsymbol{X}_{t}\right) \\ &= \begin{cases}\sum_{j=1}^{p} a_{j} X_{t+1-j}& k=1 & \\ \sum_{j=1}^{k-1} a_{j} \hat{X}_{t}(k-j)+\sum_{j=k}^{p} a_{j} X_{t+k-j}, & 1
预测的 ( 1 − α ) (1-\alpha) (1−α) 的置信区间为
( x ^ t ( k ) ± z α 2 ( 1 + g 1 2 + ⋯ + g k − 1 2 ) 1 2 σ ) \left(\hat{x}_{t}(k) \pm z_{\frac{\alpha}{2}}\left(1+g_{1}^{2}+\cdots+g_{k-1}^{2}\right)^{\frac{1}{2}} \sigma\right) (x^t(k)±z2α(1+g12+⋯+gk−12)21σ)
式中 z α 2 z_{\frac{\alpha}{2}} z2α 表示标准正态分布的上 α 2 \frac{\alpha}{2} 2α 分位数.
程序源代码
%% 预测
step = 150;
% 计算 AR(2) 的 Green 系数
g = zeros(step,1);
g(1) = 1;
g(2) = a(1)*g(1);
for j = 3:step
g(j) = a(1)*g(j-1) + a(2)*g(j-2);
end
Yf_1 = forecast(mdl,smooth_data,step);
Yf_2 = zeros(N,1);
Yf_2(1:length(smooth_data))=smooth_data;
YMSE = zeros(N,1);
for k =length(TrainData)+1:length(TrainData)+step
Yf_2(k) = Yf_2(k-OptimalARLags_BIC:k-1)'*flipud(a(1:length(mdl.Report.Parameters.ParVector)));
YMSE(k) = sum(g(1:k-length(TrainData)).^2)*var(epsilon);
end
error = Yf_1-Yf_2(length(smooth_data)+1:end);
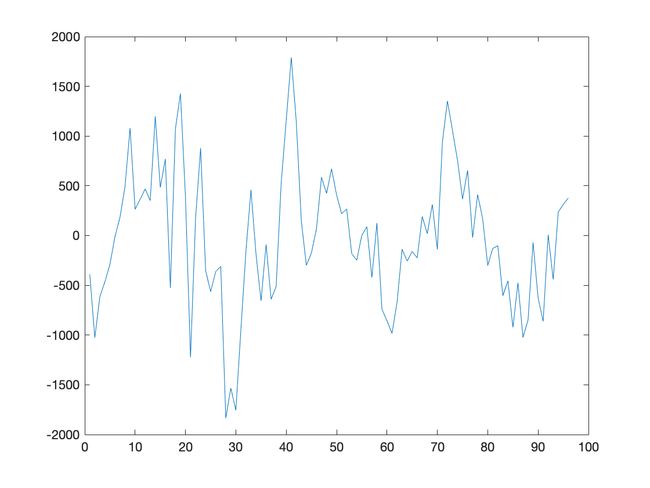
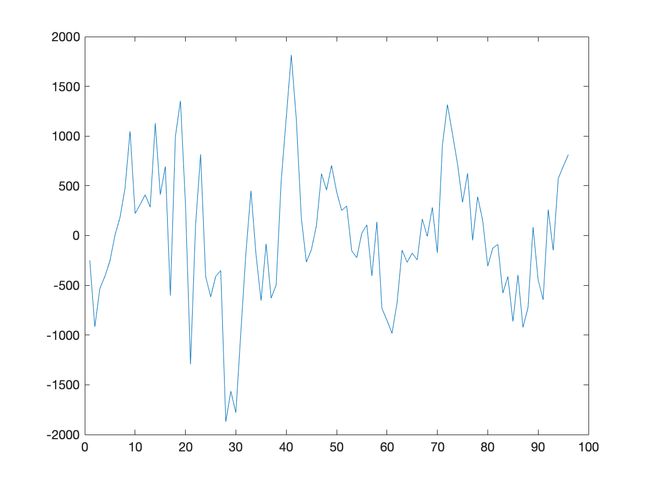
figure(8)
plot(error)
ylabel('差值')
max_error = max(error);
fprintf('最大模范数:%f\n',max_error);
upper = Yf_2 + 1.96*sqrt(YMSE);
lower = Yf_2 - 1.96*sqrt(YMSE);
figure(9)
h1 = plot(data,'b');
hold on
h2 = plot(trg + 1:trg + step,Yf_2(trg + 1:trg + step),'r','LineWidth',2);
h3 = plot(trg + 1:trg + step,upper(trg + 1:trg + step),'k--','LineWidth',1.5);
plot(trg + 1:trg + step,lower(trg + 1:trg + step),'k--','LineWidth',1.5);
title('预测结果(95% 置信区间)')
ylabel('成交量')
legend([h1,h2,h3],'原始数据','预测值','95% 置信区间','Location','NorthWest')
hold off
命令行窗口输出
最大模范数:0.000000
可以看到调用
Matlab自带的预测函数forecast与使用作者根据最佳线性预测公式计算的预测值残差达到 1 0 − 13 10^{-13} 10−13 量级, 由此可以验证此部分程序的正确性.
可以看到未来走势在 95 % 95\% 95% 置信区间内.
修正预测
预测的步长越长, 末知信息就越多, 从而估计的精度就越差. 然而, 随着时间的发展, 我们在原有的观测值 { ⋯ , x t − 1 , x t } \left\{\cdots, x_{t-1}, x_{t}\right\} {⋯,xt−1,xt} 的基础上, 不断获得新的观测 值 { x t + 1 , x t + 2 , ⋯ } \left\{x_{t+1}, x_{t+2}, \cdots\right\} {xt+1,xt+2,⋯}. 这些新观测值带来更多的信息, 从而预测末来时刻的末知信息逐渐减少. 因此, 利用新观测值的信息, 我们可以更好地预测末来的序列值 x t + k x_{t+k} xt+k, 预测精度将提高. 这就是所谓的修正预测.
修正预测有两种处理方式. 一种处理方法是把新的观测值和原数据合并, 重新拟合模型, 然后再利用拟合后的模型预测 x t + k x_{t+k} xt+k; 另一种处理方法是利用原 来的拟合模型, 然后利用新观测值修正原来的拟合模型, 从而得到新的拟合模型. 当新的观测序列很多时或易于操作时, 可采用第一种方法. 然而, 当新的观 测并不多时, 第一种方法不是最佳选择. 此时, 第二种方法将更加简便. 下面介绍第二种处理方法.
一般地, 假如获得新观测值 x t + 1 , ⋯ , x t + l ( 1 ⩽ l < k ) x_{t+1}, \cdots, x_{t+l}(1 \leqslant l
x ^ t + 1 ( k − 1 ) = g k − l ε t + l + ⋯ + g k − 1 ε t + 1 + g k ε t + g k + 1 ε t − 1 + ⋯ = g k − l ε t + l + ⋯ + g k − 1 ε t + 1 + x ^ t ( k ) \begin{aligned} \hat{x}_{t+1}(k-1) &=g_{k-l} \varepsilon_{t+l}+\cdots+g_{k-1} \varepsilon_{t+1}+g_{k} \varepsilon_{t}+g_{k+1} \varepsilon_{t-1}+\cdots \\ &=g_{k-l} \varepsilon_{t+l}+\cdots+g_{k-1} \varepsilon_{t+1}+\hat{x}_{t}(k) \end{aligned} x^t+1(k−1)=gk−lεt+l+⋯+gk−1εt+1+gkεt+gk+1εt−1+⋯=gk−lεt+l+⋯+gk−1εt+1+x^t(k)
其中 ε t + j = x t + j − x ^ ( t + j − 1 ) + 1 ( 1 ⩽ j ⩽ l ) \varepsilon_{t+j}=x_{t+j}-\hat{x}_{(t+j-1)+1}(1 \leqslant j \leqslant l) εt+j=xt+j−x^(t+j−1)+1(1⩽j⩽l) 为 x t + j x_{t+j} xt+j 的一步预测误差. 此时, 修正后的预测方差为
Var ( e t + l ( k − l ) ) = ( 1 + g 1 2 + ⋯ + g k − l − 1 2 ) σ 2 . \operatorname{Var}\left(e_{t+l}(k-l)\right)=\left(1+g_{1}^{2}+\cdots+g_{k-l-1}^{2}\right) \sigma^{2} . Var(et+l(k−l))=(1+g12+⋯+gk−l−12)σ2.
从上面的分析可知, 当我们获得新的观测值时, 修正后的预测方差将减少, 从而提高了预测精度. 而且这种修正方式简单, 易于操作.
程序源代码
%% 修正预测
step = 150;
% 计算 AR(2) 的 Green 系数
g = zeros(N,1);
g(N-step + 1) = 1;
g(N-step + 2) = a(1)*g(N-step + 1);
for j = N-step + 3:N
g(j) = a(1)*g(j-1) + a(2)*g(j-2);
end
% Revised_forecast = forecast(mdl,smooth_data,step);
Revised_forecast = zeros(N,1);
Revised_forecast(1:length(smooth_data))=smooth_data;
YMSE = zeros(N,1);
epsilon_hat = zeros(N,1);
for l = 1:120
for k =length(TrainData)+1:length(TrainData)+l
Revised_forecast(k) = Revised_forecast(k-OptimalARLags_BIC:k-1)'*flipud(a(1:length(mdl.Report.Parameters.ParVector)));
epsilon_hat(k) = TestData(k-length(TrainData)) - Revised_forecast(k);
end
for k =length(TrainData)+1:length(TrainData)+step
Revised_forecast(k) = Revised_forecast(k-OptimalARLags_BIC:k-1)'*flipud(a(1:length(mdl.Report.Parameters.ParVector)));
Revised_forecast(k) = Revised_forecast(k) + g(k+1-l:k+1-1)'*flipud(epsilon_hat(length(TrainData)+1:length(TrainData)+l));
YMSE(k) = sum(g(1:k).^2)*var(epsilon);
end
upper = Revised_forecast + 1.96*sqrt(YMSE);
lower = Revised_forecast - 1.96*sqrt(YMSE);
figure(10)
h1 = plot(data,'b');
hold on
h2 = plot(trg + 1:trg + step,Revised_forecast(trg + 1:trg + step),'r','LineWidth',2);
h3 = plot(trg + 1:trg + step,upper(trg + 1:trg + step),'k--','LineWidth',1.5);
plot(trg + 1:trg + step,lower(trg + 1:trg + step),'k--','LineWidth',1.5);
title(['获得 ',num2str(l),' 个新观测值后修正预测结果(95% 置信区间)'])
ylabel('成交量')
legend([h1,h2,h3],'原始数据','预测值','95% 置信区间','Location','NorthWest')
hold off
getframe;
end
参考文献
[1] 周永道,王会琦,吕王勇. 时间序列分析及应用. 北京:高等教育出版社,2015.
[2] 江渝,李幸,卓金武. MATLAB时间序列方法与实践. 北京:电子工业出版社,2019.
[3] 茆诗松,程依明,濮晓龙. 概率论与数理统计教程. 北京:高等教育出版社,2011.
本人非统计专业,若有不妥之处, 恳请批评指正.
作者: 图灵的猫
作者邮箱: [email protected]