Python机器学习05——判别分析
本系列所有的代码和数据都可以从陈强老师的个人主页上下载:Python数据程序
参考书目:陈强.机器学习及Python应用. 北京:高等教育出版社, 2021.
本系列基本不讲数学原理,只从代码角度去让读者们利用最简洁的Python代码实现机器学习方法。
与逻辑回归类似,判别分析是用来做分类的。判别分析也是比较经典的多元统计分析方法。它有点类似于主成分,尽可能的将数据从不同的方向投影开,因此判别分析还具有降维的功能。判别分析有判别函数和系数,根据判别函数的不同,可以分为线性判别和二次判别。最初的判别分析是用来做分类的,后来也推广到可以做多分类,目前好像不能用于回归问题。
判别分析Python案例:
导入sklearn包,本次采用鸢尾花数据集,因为判别分析提出的时候就是采用 的这个数据集验证其有效性的。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
from sklearn.metrics import cohen_kappa_score
iris = load_iris() #加载数据
dir(iris) #查看数据里面的东西
iris.feature_names #查看特征变量x的名称
iris.feature_names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width'] #重命名
X = pd.DataFrame(iris.data, columns=iris.feature_names) #变为数据框
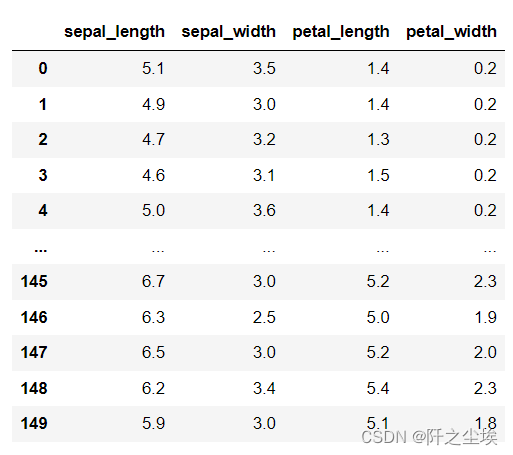
print(X)可以看到是150个样本,四个特征变量,下面画出相关系数热力图:
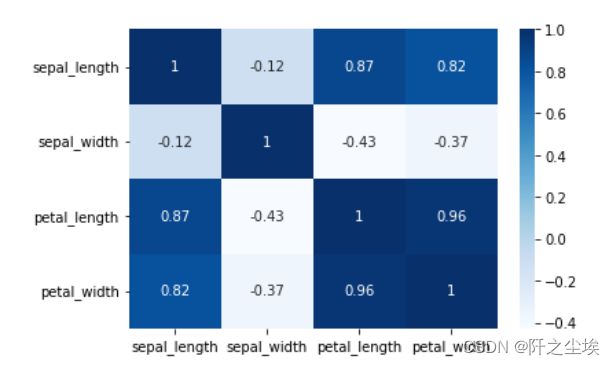
X.corr()
sns.heatmap(X.corr(), cmap='Blues', annot=True)查看y的取值,只有三种鸢尾花
y = iris.target
y开始判别分析!
model = LinearDiscriminantAnalysis()
model.fit(X, y) #拟合
model.score(X, y) #计算预测精度
#先验概率
model.priors_
#特征变量分组均值
model.means_
#线性判元对于组间方差的贡献
model.explained_variance_ratio_
#线性判元的估计系数
model.scalings_
#变为数据框展示
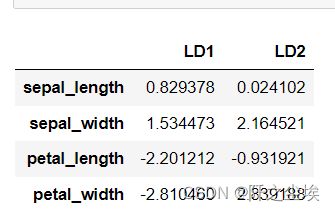
lda_loadings = pd.DataFrame(model.scalings_, index=iris.feature_names, columns=['LD1', 'LD2'])
lda_loadings画出每个样本的线性判别得分
lda_scores = model.fit(X, y).transform(X) #或lda_scores = model.fit_transform(X, y)
lda_scores.shape
lda_scores[:5, :]
LDA_scores = pd.DataFrame(lda_scores, columns=['LD1', 'LD2'])
LDA_scores['Species'] = iris.target
LDA_scores.head()
d = {0: 'setosa', 1: 'versicolor', 2: 'virginica'}
LDA_scores['Species'] = LDA_scores['Species'].map(d)
LDA_scores.head()
sns.scatterplot(x='LD1', y='LD2', data=LDA_scores, hue='Species')可以看出LD1这个维度上很好区分不同的鸢尾花品种。
下面只采用两个特征变量,直观的画出线性判别的决策边界
X2 = X.iloc[:, 2:4]
model = LinearDiscriminantAnalysis()
model.fit(X2, y)
model.score(X2, y)
model.explained_variance_ratio_
from mlxtend.plotting import plot_decision_regions
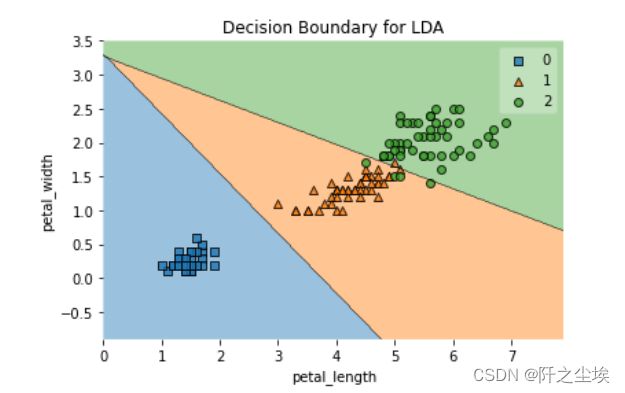
plot_decision_regions(np.array(X2), y, model)
plt.xlabel('petal_length')
plt.ylabel('petal_width')
plt.title('Decision Boundary for LDA')二次判别分析
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, stratify=y, random_state=123)
model = QuadraticDiscriminantAnalysis()
model.fit(X_train, y_train)
model.score(X_test, y_test) # Accuracy
prob = model.predict_proba(X_test)
prob[:3]
pred = model.predict(X_test)
pred[:5]
confusion_matrix(y_test, pred)
print(classification_report(y_test, pred))
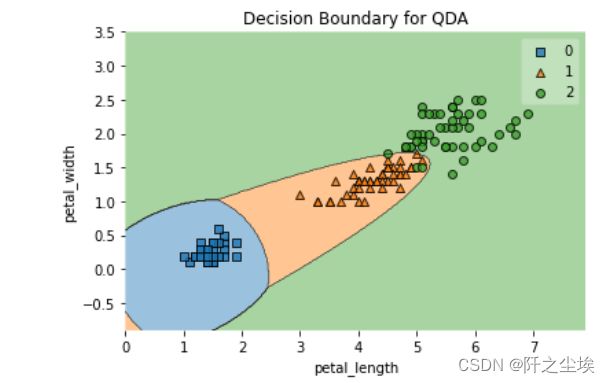
cohen_kappa_score(y_test, pred)同样选取两个特征变量进画出其决策边界
X2 = X.iloc[:, 2:4]
model = QuadraticDiscriminantAnalysis()
model.fit(X2, y)
model.score(X2, y)
plot_decision_regions(np.array(X2), y, model)
plt.xlabel('petal_length')
plt.ylabel('petal_width')
plt.title('Decision Boundary for QDA')
判别分析用于降维
线性判别类似主成分可以降维,但是不同的是线性判别利用了标签y的信息。并且降维后的数据也是原始数据的线性组合,失去了其意义,不好解释。下面将鸢尾花四个特征变为2个特征。
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
model=LDA(n_components=2)
model.fit_transform(X,y)