支持向量机算法模型

前言

从这一期开始，我们准备介绍一系列经典机器学习算法模型，主要包括逻辑回归，支持向量机，决策树，因子分析，主成分分析，K-Means聚类，多元线性回归，时间序列，关联规则，朴素贝叶斯，隐式马尔可夫，协同过滤，随机森林，XGBoost，LightGBM等，一般会涵盖算法模型的引入背景，算法模型依赖的数学原理，算法模型的应用范围，算法模型的优缺点及改进建议，工程实践案例等。既适合刚入门机器学习的新手，也适合有一定基础想要进一步掌握算法模型核心要义的读者，其中不免会涵盖许多数学符号，公式以及推导过程，如果你觉得晦涩难懂，可以来"三行科创"微信交流群和大家一起讨论交流。

从数据的线性可分到间隔最大化

支持向量机(support vector machine)是一种经典的二分类算法模型，因其严谨的数学理论和稳健的性能表现，在工程实践中一直备受青睐。这一期我们就来讨论一下支持向量机的算法模型。先从数据的线性可分开始，假设一个既包含正性样本又包含负性样本的数据集

$$D=\{(X_1,y_1),(X_2,y_2),\cdots ,(X_m,y_m)\}$$

其中, $X_i$ 表示第i个样本的特征向量，$y_i$表示第i个样本的类别标签，$y_i=+1$时表示 $(X_i,y_i)$ 为正性样本，$y_i=-1$表示 $(X_i,y_i)$ 为负性样本，如果能够找到一个超平面

$$w\cdot X+b=0$$

使得这个数据集的正性样本和负性样本完全分离开来，其中，$w$为超平面的法向量，b为超平面的截距，即对所有的$y_i=+1$的样本有$w\cdot X_i+b>0$, 对所有的$y_i=-1$的样本有 $w\cdot X_i+b<0$, 那么就称这个数据集是线性可分的，反之，则称为线性不可分，如不特别申明，本文讨论的数据集均指线性可分的。

图1 线性可分

从线性可分的定义可以看到，线性可分数据肯定能够找到一个分离超平面将其一分为二，而且这样的分离超平面不止一个，有无穷多个，支持向量机算法模型的任务就是去找一个最适合的分离超平面，使其满足

• 能够将正性样本和负性样本分离开来；
• 正性样本与负性样本的间隔最大；

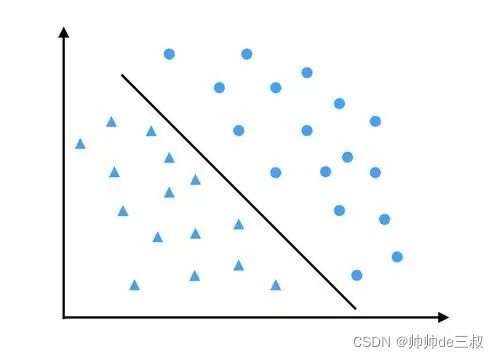
满足这样条件的超平面也称为最大间隔分离超平面，其中，第一点比较好理解，就是这个超平面能够把正性样本和负性样本完全分离开来，使得正性样本落在超平面的一边，负性样本落在超平面的另一边，以保证分离的正确性；第二点，这个间隔可以这么去想，因为分离超平面有无穷多个，那么给定一个方向(法向量)就会形成一个分离超平面簇，有些簇厚，而有些簇薄，可以把间隔大小等同于簇的厚薄，簇越厚间隔越大，簇越薄间隔越小，以下图为例进行举例说明

图2 间隔厚薄

超平面A所在的分离超平面簇很厚（A所在的阴影部分），其间隔就大，超平面B所在的分离超平面簇很薄（B所在的阴影部分），其间隔就小，用一个最厚的超平面簇来分离正性样本和负性样本，那么分错的可能性就小，具有很好的可信度。同时，可以看到分离超平面簇只与某些靠的近的样本点有关，而与其他样本点无关，这些与分离超平面簇靠得最近的样本点称为支持向量，好比用这些点来支撑起分离超平面簇，这也是为什么支持向量机要叫支持向量机，取最厚分离超平面簇中的正中间位置的一个超平面作为代表分离超平面，可以证明这个代表超平面具有间隔最大性，可以使得正性样本与负性样本的间隔达到最大。

这是在分离超平面簇确定的前提下来进行的，实现中，我们只有样本点，需要从样本点出发来找到这个间隔最大的分离超平面，为此，我们需要找一些度量，先从二维平面的距离开始。高中数学告诉我们点$(x_0,y_0)$到直线$ax+by+c=0$的距离公式

$$d=\frac{|a{x}_0+b{y}_0+c|}{\sqrt{a^2+b^2}}$$
一般的，在n维欧式空间里，点$X_0$到超平面$w\cdot X+b=0$的距离公式

$$d=\frac{|w\cdot X_0+b|}{\Vert w\Vert }$$

其中，$|w\cdot X_0+b|$ 是取绝对值， $\Vert w\Vert$为 $w$ 的$L_2$范数，有了距离公式后，我们就可以计算出所有样本点到分离超平面的距离，具体的，样本点$(X_i,y_i)$到分离超平面$w\cdot X+b=0$的距离

$$d_i=\frac{|w\cdot X_i+b|}{\Vert w\Vert }$$

为了去掉绝对值运算，我们可以分情况讨论，当样本点在超平面法向量正方向时候
$$d_i=\frac{(w\cdot X_i+b)}{\Vert w\Vert }$$

当样本点在超平面法向量反方向时候

$$d_i=\frac{-(w\cdot X_i+b)}{\Vert w\Vert }$$

为此，引入 $y_i$ 当作符号标识，上面两种情况可以统一起来

$$d_i=\frac{y_i(w\cdot X_i+b)}{\Vert w\Vert }$$

现对所有样本点$i=1,2,\cdots ,m$, 取最小值

$$d=\underset{i=1,2,\cdots ,m}{\min }{d}_i=\underset{i=1,2,\cdots ,m}{\min }\frac{y_i(w\cdot X_i+b)}{\Vert w\Vert }$$

上式称为数据集关于超平面的几何间隔， 从下图可以很直观的看到几何间隔就是支持向量到分离超平面的距离。

图3 引垂线段

现在让$w$和$b$同时扩大 $\lambda$ 倍数，计算此时的几何间隔

$$d=\underset{i=1,2,\cdots ,m}{\min }{d}_i=\underset{i=1,2,\cdots ,m}{\min }\frac{y_i(\lambda w\cdot X_i+\lambda b)}{\Vert \lambda w\Vert }=\underset{i=1,2,\cdots ,m}{\min }\frac{y_i(w\cdot X_i+b)}{\Vert w\Vert }$$
这说明了几何间隔对超平面的参数扩倍不影响，于是，我们可以去调整超平面得法向量和截距来最大化这个几何间隔

$$\underset{w,b}{\max }d=\underset{w,b}{\max }\underset{i=1,2,\cdots ,m}{\min }{d}_i$$

把问题改写成如下带约束的最优化形式

$$\begin{array}{rlr}& \underset{w,b}{\max }d& \\ & & \\ & s.t.\frac{y_i(w\cdot X_i+b)}{\Vert w\Vert }>=d,i=1,2,\cdots ,m& \end{array}$$

其中，约束条件表示每一个样本点到超平面的距离都不小于这个几何间隔，将上面约束条件稍微改写一下
$$\begin{array}{rlr}& \underset{w,b}{\max }d& \\ & & \\ & s.t.y_i(w\cdot X_i+b)>=d\Vert w\Vert ,i=1,2,\cdots ,m& \end{array}$$

由前面的计算知道，超平面参数扩倍并不会影响几何间隔，可以保持样本点的不变性，不妨令$d\Vert w\Vert =1$, 则 $d=\frac{1}{\Vert w\Vert }$，上面最优化问题可以改写成
$$\begin{array}{rlr}& \underset{w,b}{\max }\frac{1}{\Vert w\Vert }& \\ & & \\ & s.t.y_i(w\cdot X_i+b)>=1,i=1,2,\cdots ,m& \end{array}\text{\hspace{1em}(0)}$$

其中，约束条件称为样本点$(X_i，y_i)$ 的函数距离大于等于 1，上式可以等价改写成如下条件极值，这是一种凸二次规划问题
$$\begin{array}{rlr}& \underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2& \\ & & \\ & s.t.y_i(w\cdot X_i+b)-1>=0,i=1,2,\cdots ,m& \end{array}\text{\hspace{1em}(1)}$$

这就有了支持向量机的最大间隔的表现形式，也称为硬间隔最大化。

对偶算法

高等数学告诉我们解决诸如这种多元函数极值问题直接求解在代换的时候会变得异常复杂，有时候甚至没法直接求解，这时候可以采用拉格朗日乘数法，转向求解与之对应的对偶问题，通过解对偶问题而得到原始问题（1）的解，为此引入拉格朗日乘子 ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_m$，$({\lambda }_i\ge 0)$，定义拉格朗日函数

$$\mathcal{L}(w,b,\lambda )=\frac{1}{2}\Vert w{\Vert }^2-\sum _{i=1}^m{\lambda }_i[y_i(w\cdot X_i+b)-1]$$

令

$${\theta }_{\lambda }(w,b)=\underset{\lambda }{\max }\mathcal{L}(w,b,\lambda )$$
等式右边是求$\mathcal{L}(w,b,\lambda )$关于$\lambda$ 的极大，得到一个关于 $w,b$ 的函数，记作 ${\theta }_{\lambda }(w,b)$。现在来考虑一下${\theta }_{\lambda }(w,b)$取值的可能性，如果原条件不成立，即存在某个$i$ 使得 $y_i(w\cdot X_i+b)-1<0$，此时，取${\lambda }_i$为$+\infty$, 其余 ${\lambda }_i=0$，那么就有

$${\theta }_{\lambda }(w,b)=\underset{\lambda }{\max }\{\frac{1}{2}\Vert w\Vert -\sum _{i=1}^m{\lambda }_i[y_i(w\cdot X_i+b)-1]\}=+\infty$$

如果原条件成立，即对所有的 $i$ 都有$y_i(w\cdot X_i+b)-1>=0$，那么就有

$${\theta }_{\lambda }(w,b)=\underset{\lambda }{\max }\{\frac{1}{2}\Vert w\Vert -\sum _{i=1}^m{\lambda }_i[y_i(w\cdot X_i+b)-1]\}=\frac{1}{2}\Vert w\Vert$$

因此

$${\theta }_{\lambda }(w,b)=\{\begin{array}{l}\frac{1}{2}\Vert w\Vert ,原始问题条件满足\\ \\ +\infty ，原始问题的条件不满足\end{array}$$

原始问题（1）的目标函数可以改成

$$\underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2=\underset{w,b}{\min }{\theta }_{\lambda }(w,b)=\underset{w,b}{\min }\underset{\lambda }{\max }\mathcal{L}(w,b,\lambda )\text{\hspace{1em}(2)}$$

现在我们写出其对偶形式
$$\underset{\lambda }{\max }\underset{w,b}{\min }\mathcal{L}(w,b,\lambda )\text{\hspace{1em}(3)}$$
在满足KKT的条件下，下面等式成立

$$d^{\ast }=\underset{\lambda }{\max }\underset{w,b}{\min }\mathcal{L}(w,b,\lambda )=\underset{w,b}{\min }\underset{\lambda }{\max }\mathcal{L}(w,b,\lambda )=p^{\ast }$$

其中， $d^{\ast }$ 是对偶问题的解，$p^{\ast }$ 是原始问题的解，现在我们来看对偶问题

$$\underset{\lambda }{\max }\underset{w,b}{\min }\mathcal{L}(w,b,\lambda )$$

这是一个极小极大问题，可以看成先求拉格朗日函数 $\mathcal{L}(w,b,\lambda )$关于 $w,b$ 的极小，再求结果$\underset{w,b}{\min }\mathcal{L}(w,b,\lambda )$关于$\lambda$ 的极大，具体的

首先，求 $\underset{w,b}{\min }\mathcal{L}(w,b,\lambda )$

分别求其关于$w,b$ 的偏导数，并令偏导数等于0，

$$\{\begin{array}{ll}\frac{\partial \mathcal{L}(w,b,\lambda )}{\partial w}& =w-\sum _{i=1}^m{\lambda }_i{y}_i{X}_i=0\\ \frac{\partial \mathcal{L}(w,b,\lambda )}{\partial b}& =-\sum _{i=1}^m{\lambda }_i{y}_i=0\end{array}$$
由上式首先解得 $w=\sum _{i=1}^m{\lambda }_i{y}_i{X}_i$，将其代入原拉格朗日函数，此时关于 $\lambda$ 的函数

$$\begin{array}{rl}\mathcal{L}(w,b,\lambda )& =\frac{1}{2}\Vert w\Vert -\sum _{i=1}^m{\lambda }_i[y_i(w\cdot X_i+b)-1]\\ & =\frac{1}{2}(\sum _{i=1}^m{\lambda }_i{y}_i{X}_i)(\sum _{j=1}^m{\lambda }_j{y}_j{X}_j)+\sum _{i=1}^m{\lambda }_i\\ & =\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\lambda }_i{\lambda }_j{y}_i{y}_j{X}_i{X}_j+\sum _{i=1}^m{\lambda }_i\end{array}$$

即 $\underset{w,b}{\min }\mathcal{L}(w,b,\lambda )=\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\lambda }_i{\lambda }_j{y}_i{y}_j{X}_i{X}_j+\sum _{i=1}^m{\lambda }_i$，

其次，求 $\underset{w,b}{\min }\mathcal{L}(w,b,\lambda )$ 关于 $\lambda$ 的极大值，即得对偶问题

$$\begin{array}{rlr}& \underset{\lambda }{\max }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\lambda }_i{\lambda }_j{y}_i{y}_j{X}_i{X}_j+\sum _{i=1}^m{\lambda }_i& \\ & & \\ & s.t.\sum _{i=1}^m{\lambda }_i{y}_i=0& \\ & & \\ & {\lambda }_i\ge 0,i=1,2,\cdots ,m& \end{array}\text{\hspace{1em}(4)}$$

将上式求极大转换成求极小，得到与之等价的对偶问题

$$\begin{array}{rlr}& \underset{\lambda }{\min }-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\lambda }_i{\lambda }_j{y}_i{y}_j{X}_i{X}_j-\sum _{i=1}^m{\lambda }_i& \\ & & \\ & s.t.\sum _{i=1}^m{\lambda }_i{y}_i=0& \\ & & \\ & {\lambda }_i\ge 0,i=1,2,\cdots ,m& \end{array}\text{\hspace{1em}(5)}$$

假设${\lambda }^{\ast }=({\lambda }_1^{\ast },{\lambda }_2^{\ast },\cdots ,{\lambda }_m^{\ast })$ 是对偶问题（5）的解，现在利用KKT条件列出下面方程组

$$\{\begin{array}{l}\frac{\partial \mathcal{L}(w,b,\lambda )}{\partial w}=w-\sum _{i=1}^m{\lambda }_i^{\ast }{y}_i{X}_i=0\\ \frac{\partial \mathcal{L}(w,b,\lambda )}{\partial b}=-\sum _{i=1}^m{\lambda }_i^{\ast }{y}_i=0\\ {\lambda }_i^{\ast }(y_i(w{X}_i+b)-1)=0，\\ y_i(w{X}_i+b)-1\ge 0，\\ {\lambda }_i^{\ast }\ge 0，\end{array}$$
解得
$$w^{\ast }=\sum _{i=1}^m{\lambda }_i^{\ast }{y}_i{X}_i\text{\hspace{1em}(6)}$$

再取某个 ${\lambda }_j^{\ast }>0$ 和 $w^{\ast }$代入第四个等式中

$$\begin{array}{rl}& y_j(w^{\ast }{X}_j+b)-1)\\ & =y_j(\sum _{i=1}^m{\lambda }_i^{\ast }{y}_i{X}_i{X}_j+b)-1\\ & =\sum _{i=1}^m{\lambda }_i^{\ast }{y}_i{y}_j{X}_i{X}_j+y_{j}b-1\\ & =0\end{array}$$

解得
$$\begin{array}{r}{b}^{\ast }=1/y_j-\sum _{i=1}^m{\lambda }_i^{\ast }{y}_i{X}_i{X}_j=y_j-\sum _{i=1}^m{\lambda }_i^{\ast }{y}_i{X}_i{X}_j\end{array}\text{\hspace{1em}(7)}$$

此时，分离超平面就可以由下面式子给出

$$w^{\ast }X+b^{\ast }=0$$

从(6)和（7）可以看到分离超平面的参数 $w^{\ast },b^{\ast }$只与拉格朗日乘子，样本特征和标签有关，而与其他变量无关，同样，决策函数可由下式给出

$$f(X)=sign(w^{\ast }X+b^{\ast })$$

这是一个符号函数，当 $w^{\ast }X+b^{\ast }<0$ 时， $f(X)=-1$， 当 $w^{\ast }X+b^{\ast }>0$时， $f(X)=1$。

这样，线性可分数据的支持向量机算法模型就出来了，称为线性可分支持向量机，而现实中很少有数据集是线性可分的，大多是线性不可分的或者近似线性可分的，下面来分别介绍线性支持向量机算法模型和非线性支持向量机算法模型。

线性支持向量机与非线性支持向量机

假设数据集不是线性可分的，而是近似线性可分的，有一些特异点，将这些特异点去除之后，剩下的样本点就是线性可分的。

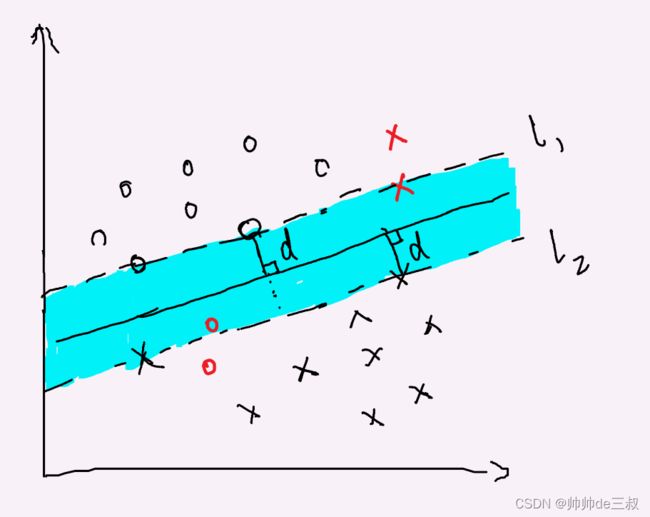
如上图所示，将4个红色样本点去掉后就变成线性可分，而红色样本点不能满足约束条件
$$y_i(w{X}_i+b)\ge 1$$

为此，给每一个样本点引入一个松弛变量 ${\xi }_i\ge 0$， 使得样本点$(x_i,y_i)$的函数距离加上不同的松弛变量之后大于等于 1

$$y_i(w{X}_i+b)+{\xi }_i\ge 1$$
其中，已经满足约束条件的松弛变量 ${\xi }_i=0$，而特异点的松弛变量 ${\xi }_i\ge 0$， 从而使得所有的样本点满足约束条件，但是引入松弛变量需要使得构造结构变得复杂一些，于是，目标函数追加结构成本，这样，目标函数就变成了

$$\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^m{\xi }_i$$

其中，$C\sum _{i=1}^m{\xi }_i$ 称为结构成本函数，$C>0$ 称为惩罚系数，表示对误分类的惩罚，$C$ 越大对误分类惩罚越严重，$C$ 越小对误分类惩罚越轻，于是，线性支持向量机问题就可以写成如下形式

$$\begin{array}{rlr}& \underset{w,b,\xi }{\min }\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^m{\xi }_i& \\ & & \\ & s.t.y_i(w\cdot X_i+b)>=1-{\xi }_i,i=1,2,\cdots ,m& \\ & & \\ & {\xi }_i\ge 0,i=1,2,\cdots ,m& \end{array}\text{\hspace{1em}(1)}$$

线性支持向量机也有其对偶学习算法，这里不表。有时候分类问题不是简单线性的，这时候就需要用到非线性支持向量机

其核心要义是先用非线性变换将非线性问题变换成高维空间的线性问题，再在高维空间中解线性支持向量机问题，其中，核技巧为常用的方法，也有其对偶算法，这里不做深入研究。

实践案例

本文以吴恩达机器学习系列课程中的一个作业作为案例，实践操作一下支持向量机。首先，看一下数据长什么样子

原数据是一份只有51个样本点的数据集，每个样本点有2个特征和一个标签，前两列表示特征，第三列是类别标签，其中，类别标签1表示该样本点正性的，类别标签 0 表示该样本点是负性样本，将原数据可视化效果如下

从原数据分布图可以看到正性样本主要居于左下角，负性样本主要居于右上角，左上角有一个比较离群的负性样本点，除此之外，正性样本和负性样本分离的比较明显，中间有一条不宽不窄的空隙，具备线性可分性，接下来利用支持向量机算法模型将其分类

代码如下

# -*- encoding: utf-8 -*-
'''
@Project :   svm
@Desc    :   支持向量机
@Time    :   2022/06/18 17:01:34
@Author  :   帅帅de三叔,[email protected]
'''
import numpy as np  #导入数值分析模块
import scipy.io as scio #用来读取matlat数据文件
import matplotlib.pyplot as plt #导入绘图模块
import scipy.optimize #最优化
from sklearn import svm #导入支持向量机

data = scio.loadmat("D:\项目\机器学习\吴恩达机器学习课件\CourseraML\ex6\data\ex6data1.mat") #读取数据
X, y = data["X"], data["y"]
pos =  np.array([X[i] for i in range(len(X)) if y[i]==0]) #正性样本
neg = np.array([X[i] for i in range(len(X)) if y[i]==1]) #负性样本

plt.figure(figsize=(6,4)) #新建画布
plt.scatter(pos[:,0], pos[:,1], color ='green', marker='+', label = 'positive') #正性样本
plt.scatter(neg[:,0], neg[:,1], color = 'brown', marker='*', label ='negative') #负性样本
plt.legend(loc ='lower left') #图例

model = svm.SVC(C=1, kernel='linear') #支持向量机分类模型初始化
model.fit(X, y.ravel()) #模型训练

xvals = np.linspace(np.min(X[:,0])-0.1, np.max(X[:,0]+0.1), 100) #
yvals = np.linspace(np.min(X[:,1])-0.1, np.max(X[:,1]+0.1), 100) #
u, v  = np.meshgrid(xvals , yvals) #网格矩阵
X_dummy = np.c_[u.ravel(), v.ravel()] #u，v拉直并按列拼接
zvals = model.predict(X_dummy).reshape(u.shape) #生成z变量100*100
plt.contour(u, v, zvals)#等值线可视化决策边界
plt.show()

执行代码便会得到如下分类效果图

由效果图可以看到正性样本和负性样本分离的还是很干净，仅左上角的那个离群样本点被错误划分了，但是从原数据的分布图我们大体可以看到是可以找到一条直线将所有样本点完全正确分离开来，为此，将这个划分错误的点视为特异点，现在我们尝试增大惩罚系数C，让其由最初的1变成100

model = svm.SVC(C=100, kernel='linear') #支持向量机分类模型初始化

增大惩罚系数后的效果图如下

对比之前的分类效果图，验证之前的猜测，的确可以找到一条直线将正性样本与负性样本完全分离开来，可以明显的看到左上角那个离群样本点也被正确划分了，这说明增大惩罚系数，加大了对数据集分对的可能性，这时训练集的分类准确率很高，但是泛化能力很弱，反之，惩罚系数小，对错误分类的惩罚就小，允许存在错误分类，将他们当成噪声点，泛化能力就强。同时，我们还可以调整kernel核函数，之前的是 “linear”，现在换成"rbf"

model = svm.SVC(C=1, kernel='rbf') #支持向量机分类模型初始化

改变核函数后的预览效果图

同时还可以提升惩罚系数，分类效果看起来会更加匀称

model = svm.SVC(C=100, kernel='rbf') #支持向量机分类模型初始化

这个实例由最初的简单的线性划分，再到增大惩罚系数完全划分，再到改变核函数这种层层递进的方式试验完毕，支持向量机我们也告一段落，下一次，我们讨论一下决策树。

上一期：逻辑回归

参考文献
1，https://zhuanlan.zhihu.com/p/77750026
2，拉格朗日乘数
3，https://blog.csdn.net/the_lastest/article/details/78461566
4，https://zhuanlan.zhihu.com/p/33229011
5，非线性支持向量机
6，https://zhuanlan.zhihu.com/p/370857645
7，支持向量机参数