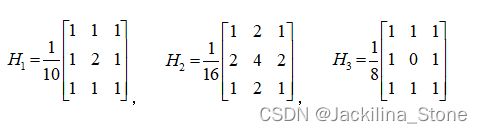数字图像处理（入门篇）九 图像数据预处理之滤波

目录

1 模板运算

（1）模板卷积

（2）模板排序

2 均值滤波

（1）代码

（2）结果图

 3 高斯滤波

 （1）代码

（2）结果图

4 中值滤波

（1）代码

（2）结果图

 5 图像锐化

（1）代码

（2）结果图

灰度变换是点处理，输出值只和指定的像素点相关。

直方图是全局处理，输出值和整幅图像相关。

空间滤波是一种局部的处理方式。像素P的输出值由输入图像中像素P 以及其邻域中的像素值确定。

1 模板运算

        常用的模板运算有模板卷积和模板排序。

（1）模板卷积

        模板滤波器是一幅尺寸为n*n的小图像，n一般为奇数。小图像中每个位置上的值为权重。在计算的时候，将模板中心和像素p对齐，选取原始图像中和模板相同范围的领域内的像素值作为输入。计算公式如下：

 上述公式中，原始图像像素灰度值为s，计算的结果为d。

（2）模板排序

       计算时将邻域中的像素值进行排序，选择特定次序的灰度值作为像素P位置的输出值。比如：最大值，最小值，中位数等。

2 均值滤波

         图像邻域平均法的优点是算法简单，计算速度快，主要缺点是在降低噪声的同时在边缘和细节处使图像产生模糊，邻域越大，模糊越严重。为了改善邻域平均滤波法的这个缺点，可以使用加权平均滤波器。常用的加权均值滤波器如下所示：

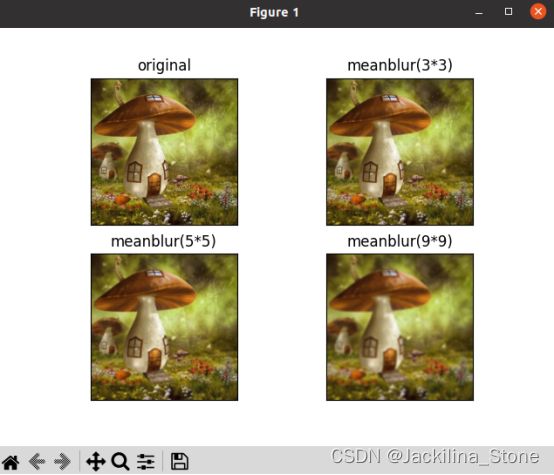
        图像邻域平均法的处理效果与所选的邻域半径有关。半径越大，则图像的模糊程度也就越大。因此在实际应用中，可以根据不同的需要来选择使用不同的模板尺寸，如3×3、5×5、7×7和9×9等。邻域平均法是最简单的一种平滑方法，噪声平滑效果较好。

（1）代码

import numpy as np
import matplotlib.pyplot as plt
import cv2
def run(img_path):
    img = cv2.imread(img_path)
    # 方法一：使用cv2.blur
    im_meanblur9 = cv2.blur(img, (9, 9))
    im_meanblur5 = cv2.blur(img, (5, 5))
    # 方法二：使用cv2.filter2D
    mean_blur = np.ones([3, 3], np.float32)/9
    im_meanblur3 = cv2.filter2D(img, -1, mean_blur)
    titles = ["original", "meanblur(3*3)", "meanblur(5*5)", "meanblur(9*9)"]
    images = [img, im_meanblur3, im_meanblur5, im_meanblur9]
    for i in range(4):
        plt.subplot(2, 2, i + 1), plt.imshow(images[i], 'gray')
        plt.title(titles[i])
        plt.xticks([]), plt.yticks([])
    plt.show()
if __name__ == '__main__':
    run("test_bgr.jpg")
    pass

（2）结果图

 3 高斯滤波

        高斯滤波（或者说“高斯模糊”）就是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。

       高斯滤波就是对整幅图像进行加权平均的过程，每一个像素点的值都由其本身和邻域内的其他像素值经过加权平均后得到的结果。

       高斯滤波处理后，整个图像相较于原始图像会看起来较为模糊，原始图像上的某些噪声点在经过周围像素点加权求和后会被剔除掉。

       高斯滤波模板根据高斯分布来确定模板系数，接近中心的权重比边缘的权重大。

 （1）代码

import numpy as np
import matplotlib.pyplot as plt
import cv2
def run(img_path):
    img = cv2.imread(img_path)
    # 方法一：使用cv2.GaussianBlur
    gaussianblur_3 = cv2.GaussianBlur(img, (3, 3), 0)
    gaussianblur_13 = cv2.GaussianBlur(img, (13, 13), 0)
    # 方法二：使用cv2.filter2D
    gaussian_blur = np.array([
        [1, 4, 7, 4, 1],
        [4, 16, 26, 16, 4],
        [7, 26, 41, 26, 7],
        [4, 16, 26, 16, 4],
        [1, 4, 7, 4, 1]], np.float32)/273
    gaussianblur_5 = cv2.filter2D(img, -1, gaussian_blur)
    titles = ["original", "gaussianblur(3*3)", "gaussianblur(5*5)", "gaussianblur(13*13)"]
    images = [img, gaussianblur_3, gaussianblur_5, gaussianblur_13]
    for i in range(4):
        plt.subplot(2, 2, i + 1), plt.imshow(images[i], 'gray')
        plt.title(titles[i])
        plt.xticks([]), plt.yticks([])
    plt.show()
if __name__ == '__main__':
    run("test_bgr.jpg")
    pass

（2）结果图

4 中值滤波

        中值滤波是由Turky于1971年提出来的。中值滤波方法是一种非线性图像降噪方法，它在含有脉冲噪声和点状噪声的图像的处理中， 处理的效果较好。

         一般在实际使用窗口时，一般先用小尺寸的窗口，然后再逐渐增大窗口的尺寸，直到中值滤波的滤波效果满意为止。即窗口尺寸一般先用3×3，再用5×5，逐渐增大直到处理效果满意为止。常用的窗口形状有线状、方形、圆形、十字形以及圆环形等等。

        相比较于均值滤波，中值滤波的降噪效果比较明显，能够较好的保留原始图像的跃变部分。在灰度值变化比较小的情况下，中值滤波有较好的平滑效果，而且使得图像边界的模糊程度有所降低。但是，在大面积的噪声污染的情况下，中值滤波的处理效果却不如均值滤波的处理效果好。这是因为在邻域中如果多数图像点都已经被噪声污染，所以中值滤波的输出仍然是被噪声污染的像素。均值滤波却在某种程度上对噪声进行了平滑处理，即求平均值运算。

        中值滤波对椒盐噪声的抑制效果好，在抑制随机噪声的同时能有效的保护图像边缘信息。但是，中值滤波是一种非线性变换，会破坏像素点间的线性关系，不适用于点、线等细节较多的图像或高精度的图像。

（1）代码

使用OpenCV的中值模糊 API。

dst=cv2.medianBlur（src,ksize）

src 源图像。可有任意数量的通道，并能对各个通道独立处理。ksize 是滤波核的大小。

import numpy as np
import matplotlib.pyplot as plt
import cv2
def run(img_path):
    img = cv2.imread(img_path)
    medianblur_3 = cv2.medianBlur(img, 3)
    medianblur_5 = cv2.medianBlur(img, 5)
    medianblur_9 = cv2.medianBlur(img, 9)
    titles = ["original", "medianblur(3*3)", "medianblur(5*5)", "medianblur(9*9)"]
    images = [img, medianblur_3, medianblur_5, medianblur_9]
    for i in range(4):
        plt.subplot(2, 2, i + 1), plt.imshow(images[i], 'gray')
        plt.title(titles[i])
        plt.xticks([]), plt.yticks([])
    plt.show()
if __name__ == '__main__':
    run("test_bgr.jpg")
    pass

（2）结果图

 5 图像锐化

        图像锐化的主要目的是突出图像中的边缘、轮廓和图像细节。最常用的是梯度法。

（1）代码

import numpy as np
import matplotlib.pyplot as plt
import cv2
def run(img_path):
    img = cv2.imread(img_path)
    sharpen_1 = np.array([
        [-1, -1, -1],
        [-1, 9, -1],
        [-1, -1, -1]])
    sharpen1_img = cv2.filter2D(img, -1, sharpen_1)
    sharpen_2 = np.array([
        [0, -1, 0],
        [-1, 8, -1],
        [0, 1, 0]])/4.0
    sharpen2_img = cv2.filter2D(img, -1, sharpen_2)
    titles = ["original", "sharpen_1", "sharpen_2"]
    images = [img, sharpen1_img, sharpen2_img]
    for i in range(3):
        plt.subplot(1, 3, i + 1), plt.imshow(images[i], 'gray')
        plt.title(titles[i])
        plt.xticks([]), plt.yticks([])
    plt.show()
if __name__ == '__main__':
    run("test_bgr.jpg")
    pass

（2）结果图