通信中的同步(一)——基于FFT的信号信号载波频偏估计
实际上,基于 F F T FFT FFT的粗同步算法适用于各种调制方式。(BPSK, QPSK, 8PSK, PAM, or QAM调制)
基本算法见 Wang, Y., K. Shi, and E. Serpedi. "Non-Data-Aided Feedforward Carrier Frequency Offset Estimators for QAM Constellations: A Nonlinear Least-Squares Approach." EURASIP Journal on Applied Signal Processing. 2004:13, pp. 1993–2001
基于 F F T FFT FFT的频偏估计算法如下:
Δ f ^ = f samp N ⋅ m arg max f ∣ ∑ k = 0 N − 1 r m ( k ) e − j 2 π k t / N ∣ , ( − R s y m 2 ≤ f ≤ R s y m 2 ) \Delta \widehat{f}=\frac{f_{\text {samp}}}{N \cdot m} \arg \max _{f}\left|\sum_{k=0}^{N-1} r^{m}(k) e^{-j 2 \pi k t / N}\right|, \quad\left(-\frac{R_{s y m}}{2} \leq f \leq \frac{R_{s y m}}{2}\right) Δf =N⋅mfsampargfmax∣∣∣∣∣k=0∑N−1rm(k)e−j2πkt/N∣∣∣∣∣,(−2Rsym≤f≤2Rsym)
其中, m m m是调制阶数(BPSK=2,QPSK=4,8PSK=8…), r ( k ) r(k) r(k)接收到的信号, R s y m R_{s y m} Rsym 为符号速率, N N N为FFT点数. 实际上,算法就是寻找序列 r m ( k ) r^m(k) rm(k)的离散傅里叶变换的峰值谱线,其对应的频率即频偏的m倍。
现在的信号处理芯片,特别是FPGA,特别适用于 F F T FFT FFT计算,因此,这种基于 F F T FFT FFT的算法适用于工程实现。
Matlab仿真
Matlab已有函数comm.CoarseFrequencyCompensator完成这个算法。
下面我们以QPSK为例,按照算法来进行仿真,并且和comm.CoarseFrequencyCompensator的结果进行比较。
仿真参数设计
| 名称 | 大小 |
|---|---|
| Number of input symbols | 2048 |
| Samples per symbol | 4 |
| Sampling frequency (Hz) | 80000 |
| mOrder | 4 |
代码部分参考Matlab的帮助文档。
clear;
clf;
close all;
% Compensate for Frequency Offset in a QPSK Signal
% Compensate for a 4 kHz frequency offset imposed on a noisy QPSK signal.
%
% Set the parameters.
nSym = 2048; % Number of input symbols
sps = 4; % Samples per symbol
nSamp = nSym*sps; % Number of samples
fs = 80000; % Sampling frequency (Hz)
mOrder = 4;
% Create a square root raised cosine transmit filter.
txfilter = comm.RaisedCosineTransmitFilter(...
'RolloffFactor',0.2, ...
'FilterSpanInSymbols',8, ...
'OutputSamplesPerSymbol',sps);
%
% Create a phase frequency offset object to introduce the 4 kHz frequency
% offset.
freqOffset = comm.PhaseFrequencyOffset(...
'FrequencyOffset',4000, ...
'SampleRate',fs);
% Generate QPSK symbols, filter the modulated data, pass the signal through
% an AWGN channel, and apply the frequency offset.
data = randi([0 mOrder-1],nSym,1);
modData = pskmod(data,mOrder,pi/mOrder);
txSig = txfilter(modData);
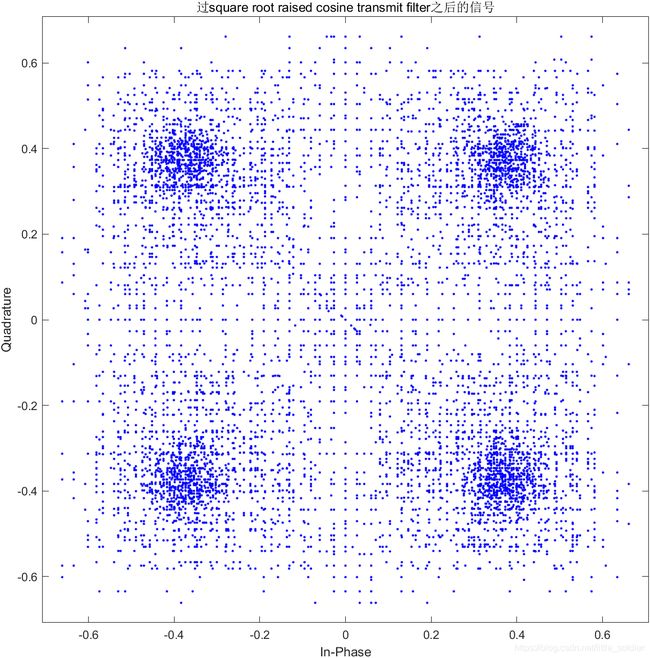
scatterplot(txSig)
title("过square root raised cosine transmit filter之后的信号")
rxSig = awgn(txSig,20,'measured');
offsetData = freqOffset(rxSig);
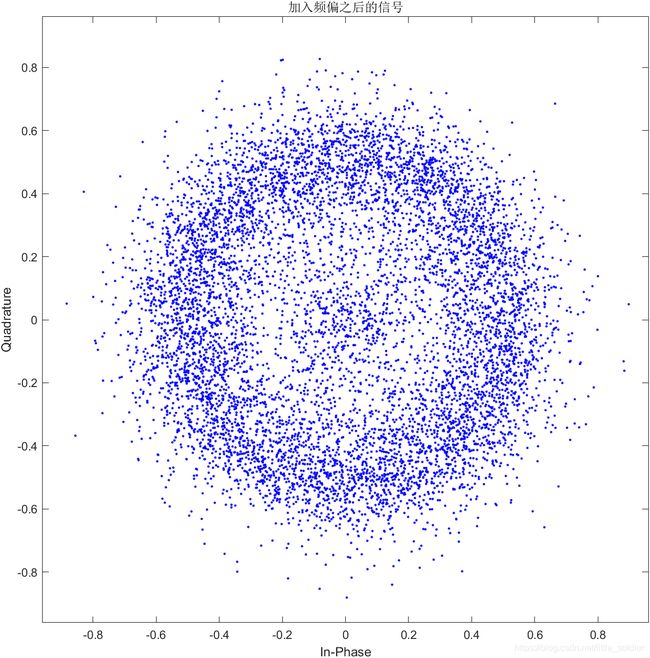
scatterplot(offsetData)
title("加入频偏之后的信号")
% 按照算法进行频偏估计
% 频率分辨率
fr = 1;
% 根据频率分辨率计算FFT点数
Nfft = 2^(floor(log2(fs/fr)));
% 计算FFT,取幅值
% 注意要对输入数据做mOrder的乘方运算将所有星座上的频偏都对应到一个值,即mOrder倍的频偏上
fftData = abs(fft(offsetData.^mOrder,Nfft));
% 作图
figure
plot(fftData);
% 寻找最大值
[maxVaule,maxIndex] = max(fftData);
% 将频率索引对应到-fs/2~fs/2上
if maxIndex>Nfft/2
maxIndex = maxIndex - Nfft;
end
% 计算频偏。注意要除以mOrder,因为在计算FFT的时候,对输入数据进行了mOrder的乘方运算
estFreqOffset1 = fs/Nfft*(maxIndex-1)/mOrder
% compensate the FreqOffset to the signal
compensatedData1 = offsetData .*exp(2*pi*j*(-estFreqOffset1)/fs*(1:nSamp)');
% 做星座图
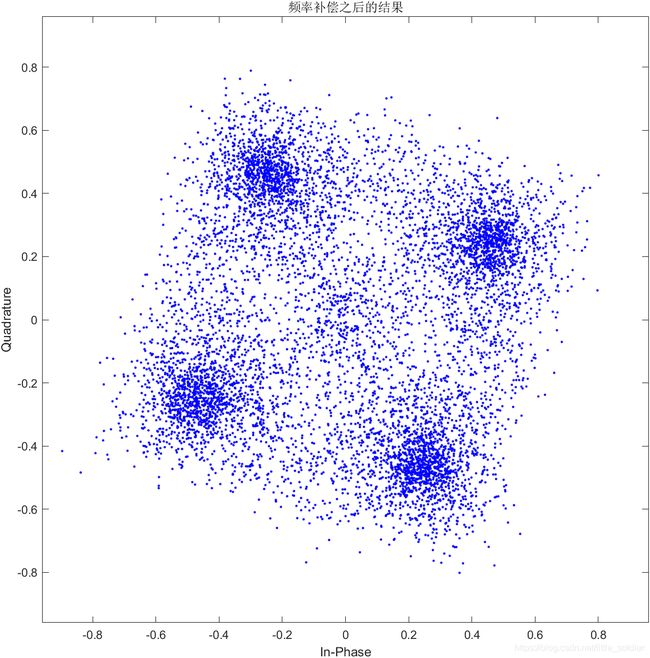
scatterplot(compensatedData1)
title("频率补偿之后的结果")
% 用matlab自带函数计算
% Create a coarse frequency compensator object to compensate for the offset.
freqComp = comm.CoarseFrequencyCompensator(...
'Modulation','QPSK', ...
'SampleRate',fs, ...
'FrequencyResolution',1);
[compensatedData2,estFreqOffset2] = freqComp(offsetData);
estFreqOffset2
% 作图
scatterplot(compensatedData2)
title("Matlab自带函数频率补偿之后的结果")
仿真结果
结论
1.根据算法写出来的程序对频偏的估计和Matlab自带函数估计的频偏完全一致。
2.在频偏估计出来之后,进行频率补偿后,从星座图中可以看出,消除了频偏带来的影响。
3.只是从星座图可以看出,本人代码的结果出现了一定的相位差,而Matlab自带函数没有这个相位差。这个问题待解决。
4.在通信接收机中,相位差问题也可以由后续的锁相环来解决。
最后
基于FFT的频偏估计方法能够很好地估计频偏,特别是在硬件条件(计算资源)允许的情况下,频偏估计的精度可以非常高。在通信接收机当中,是一种非常简便而且适用的粗同步方法。