计算机视觉入门之图像处理<五>:图像平滑处理
往期文章回顾:
计算机视觉入门之<零>
计算机视觉入门之图像处理<一>:图像处理基础概念
计算机视觉入门之图像处理<二>:图像处理基础概念
计算机视觉入门之图像处理<三>:图像插值方法
计算机视觉入门之图像处理<四>:图像直方图均衡化
文章目录
-
- 前言
- 空间域图像滤波基础
- 平滑空间滤波器
-
- 均值滤波器
- 高斯滤波器
- 中值滤波器
前言
本篇文章主要包括图像空间域滤波的基础知识,以及最基本的平滑滤波方法:均值平滑滤波、高斯平滑滤波和中值平滑滤波,在阐述其基本原理的基础上利用OpenCV简单实现。
空间域图像滤波基础
所谓的空间域就是包含图像像素的平面,空间域与频率域相对,与频率域相比,在空间域进行图像的相关处理更加容易。

如上图所示,以像素位置 ( x , y ) (x, y) (x,y)为中心的 3 ∗ 3 3*3 3∗3的矩形(不一定要是矩形,还可以是其他形状,但矩形在计算机上更易实现)范围称为 ( x , y ) (x, y) (x,y)的 3 ∗ 3 3*3 3∗3邻域。
假设输入图像为 f ( x , y ) f(x,y) f(x,y), 经过空间域中对应的处理 T T T后的图像为 g ( x , y ) g(x, y) g(x,y),即: g ( x , y ) = T [ f ( x , y ) ] g(x, y) = T[f(x, y)] g(x,y)=T[f(x,y)]式中的 T T T称为领域内图像像素操作(简单来说就是对领域内的像素进行加减乘除四则运算)
因此空间滤波器由一个邻域和像素操作 T T T构成,这里一般要求滤波器的大小为奇数,这样每一个滤波器都有一个中心点,在此基础上,滤波器的输出就等于图像中每个像素点经过滤波之后的像素值。若想要原始图像的每个像素点都进行滤波,那么滤波器的中心点就必须经过图像的每个像素点,由此便可生成滤波后的图像。

上图表示的是 3 ∗ 3 3*3 3∗3邻域线性空间滤波器的滤波机理,即: g ( x , y ) = w ( − 1 , − 1 ) ∗ f ( x − 1 , y − 1 ) + w ( − 1 , 0 ) ∗ f ( x − 1 , y ) + ⋯ g(x,y) = w(-1,-1)*f(x-1, y-1)+w(-1, 0)*f(x-1,y)+\cdots g(x,y)=w(−1,−1)∗f(x−1,y−1)+w(−1,0)∗f(x−1,y)+⋯ g ( x , y ) = ∑ s = − a a ∑ t = − b b w ( s , t ) f ( x + t , y + t ) g(x, y)=\sum_{s=-a}^{a}\sum_{t=-b}^{b}w(s,t)f(x+t, y+t) g(x,y)=s=−a∑at=−b∑bw(s,t)f(x+t,y+t)空间滤波器在图像上滑动,进行运算输出每个像素点的像素值,滤波器输出取决于邻域像素值和像素操作 T T T。
滤波器的一般要求:
- 滤波器大小一般为奇数。也可以是偶数或者是偶数和奇数混合的滤波器,一般情况下奇数尺寸的滤波器因为其中心就落在整数像素点上,因此简化了计算和操作。
- 在满足滤波需求的情况下,若滤波器系数之和为1,则滤波前后图像亮度保持不变,若系之和大于1,图像变亮;小于1,图像变暗;等于0,图像会变得非常暗。
- 对于滤波器输出的像素值,应该符合像素值要求,8比特图中,大于255的像素值,可以对256取余或者令其等于255;负数取绝对值。
平滑空间滤波器
平滑滤波器主要用于图像的模糊处理和降低图像噪声,该滤波器主要用于特征工程预处理任务中,比如Canny算法边缘提取的降噪处理。根据图像像素操作 T T T的特性可以将滤波器分为线性平滑滤波器和非线性平滑滤波器。线性平滑滤波器主要包括均值滤波器、高斯滤波器,而非线性滤波器主要包括中值滤波器。
均值滤波器
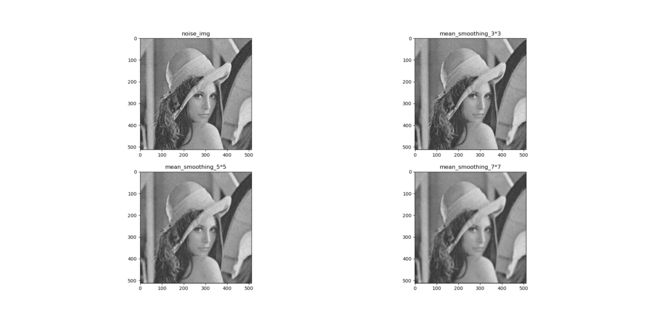
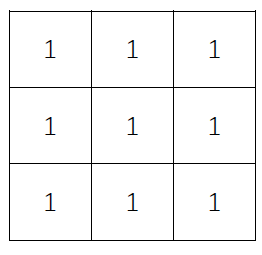
均值滤波器基本原理:滤波器的输出就是邻域内的像素值均值,使用邻域内的平均灰度来代替图像中的每个像素值。比如当前像素点的灰度值为255(白噪声),假设邻域内的灰度值不全为255, 那么取均值后当前像素点的灰度值肯定小于255,此时噪声强度就被降低了(降低了图像灰度的“尖锐”变化)。下图是 3 ∗ 3 3*3 3∗3均值滤波器模板,在每个模板前面需要乘上 1 9 \frac1 9 91(1除以所有系数之和), 5 ∗ 5 5*5 5∗5模板和 7 ∗ 7 7*7 7∗7模板与之类似
 实现代码:
实现代码:
"""图像加噪处理"""
def noise_attached(src, noise_points_num):
for i in range(noise_points_num):#noise_points_num随机噪声点个数
random_x = np.random.randint(0, src.shape[0], 1)#在图像中随机取x
random_y = np.random.randint(0, src.shape[1], 1)#在图像中随机取y
src[random_x, random_y] = np.random.choice([0, 255])#在相应的位置加入椒盐噪声(0:对应胡椒噪声;255:对应白盐噪声)
return src
"""添加高斯噪声"""
def gauss_noise_attached(src, mean, std):
img_gauss_noise = np.zeros_like(src)
for i in range(src.shape[0]):
for j in range(src.shape[1]):
gauss_num = np.random.normal(mean, std) #产生高斯随机数
img_gauss_noise[i, j] = np.where(src[i, j] + gauss_num > 255, 255, src[i, j] + gauss_num)
img_gauss_noise[i, j] = np.where(src[i, j] + gauss_num < 0, 0, src[i, j] + gauss_num)
return img_gauss_noise
def mean_smoothing(nosie_img, size):
result = np.zeros_like(nosie_img)#创建一个零矩阵,用于存储滤波后的图像
padding_img = cv.copyMakeBorder(nosie_img,
size[0]//2, size[0]//2, size[0]//2, size[0]//2,
borderType=cv.BORDER_CONSTANT, value=0)
padding_img = padding_img / 255.#图像归一化处理
print(padding_img.shape)
#zero padding
#size.shape[0]//2分别表示在图像顶部、底部、左边、右边进行zero padding的行数和列数(只针对奇数尺寸滤波器,且要求滤波器中心与图像每个像素点对齐,这点这重要)
#borderType=cv.BORDER_CONSTANT, value=0表是padding值类型为常熟,且为0
#补零操作只是为了保持滤波前后图像大小不变
# padding_img = padding_img.astype(np.uint32)#不进行归一化处理则需要进行数据类型转换,uint8->uint32:防止数值溢出
for i in range(nosie_img.shape[0]):
for j in range(nosie_img.shape[1]):
m = i + size[0] // 2
n = j + size[1] // 2
a = padding_img[m - (size[0] // 2): m + (size[0] // 2 + 1),
n - (size[0] // 2): n + (size[0] // 2 + 1)]#3*3邻域内的像素值矩阵
result[i, j] = np.round(1 / (size[0]*size[1]) * (np.sum(a))* 255.)#邻域像素矩阵均值处理,size[0]*size[1]为滤波器尺寸m*n
return result
由上图可知,均值滤波后图像中的噪声确实减少了,但随着滤波器尺寸的增大图像也逐渐模糊,因为图像的边缘是图像灰度尖锐变化带来的特性,所以滤波处理后存在边缘模糊效应,这一点对于后续的图像处理是不利的。
高斯滤波器
上面的均值滤波器中的系数都是相等的,将这些系数看作是图像中每个像素点灰度值计算时在邻域像素对应的权重,因为系数相等,所以可以视为邻域内的所有像素点对于当前像素点灰度值计算同等重要。但在实际中,因为图像具有连续性,相邻越近的像素点,和当前像素点的相似度也就越大,那么就可以认为,距离越近,对于当前像素点越重要,对应的权重系数就应越大,于是邻域像素点对应的系数就不全一样,这就是所谓的加权平均。距离当前像素点越近,系数越大,距离越远,系数越小,这一特征与二元高斯分布类似,于是采用高斯核来描述滤波器系数,因为该滤波器也称之为高斯滤波器。
二元高斯公式: f ( x , y ) = 1 2 π σ 2 e − x 2 + y 2 2 σ 2 f(x, y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}} f(x,y)=2πσ21e−2σ2x2+y2

上图中 σ \sigma σ=1, μ \mu μ=0, 在每个维度的变量上数据都呈现出高斯分布,因此利用上述公式来计算生成不同大小的高斯滤波器模板(有时上式中的系数 1 2 π σ 2 \frac{1}{2\pi\sigma^2} 2πσ21可以省略不参与计算)
实现代码:
def gauss_blur(noise_img, sigma, kernel_size):
result = np.zeros_like(noise_img) # 创建一个零矩阵,用于存储滤波后的图像
padding_img = cv.copyMakeBorder(noise_img,
kernel_size[0] // 2, kernel_size[0] // 2, kernel_size[0] // 2, kernel_size[0] // 2,
borderType=cv.BORDER_CONSTANT, value=0)#zero padding
kernel = np.zeros(kernel_size)#高斯核, kernel_size=[n, n]
"""计算高斯核"""
for i in range(kernel.shape[0]):
for j in range(kernel.shape[1]):
index = np.argwhere(kernel == kernel[i, j])#计算得出每个元素的位置
x = index[:, 0] - (kernel_size[0] // 2)#以核中心点为原点(0,0)
y = index[:, 1] - (kernel_size[1] // 2)
b = 1 / (2 * 3.14 * sigma ** 2) * np.exp(- (x ** 2 + y ** 2) / (2 * sigma ** 2))#二元高斯公式
kernel[index[:, 0], index[:, 1]] = np.round(b*100)#这里的高斯核只要要求数据在每个维度上呈现出高斯分布即可
print(kernel)
for i in range(noise_img.shape[0]):
for j in range(noise_img.shape[1]):
m = i + (kernel_size[0] // 2)
n = j + (kernel_size[1] // 2)
arr = padding_img[m - (kernel_size[0] // 2): m + (kernel_size[0] // 2 + 1),
n - (kernel_size[0] // 2): n + (kernel_size[0] // 2 + 1)] # kernel_size邻域内的像素值矩阵
result[i, j] = np.sum(arr*kernel) / np.sum(kernel)#邻域像素矩阵和高斯核对应相乘再相加,最后再除以高斯核系数之和
return result
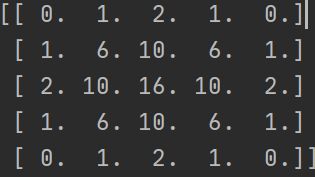
上述代码主要分为两部分,一部分是生成高斯核矩阵, 另一部分是邻域像素计算(这部分与均值滤波大同小异)下图是生成的高斯核矩阵(以 5 ∗ 5 5*5 5∗5为例, 3 ∗ 3 3*3 3∗3类似)
实现效果:
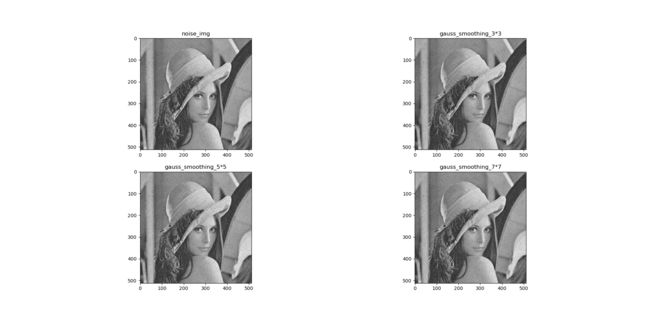
如上图所示,实现代码中 σ \sigma σ=0.1,可以清楚地看出噪声点,当 σ \sigma σ比较小时,二元高斯曲面分布将呈现瘦高型,分布曲面的斜率陡峭,数据变化较大,因此高斯曲面几乎只有原点位置有最大值,其他地方值几乎为零,高斯滤波模板中系数相差较大,对图像基本没有任何滤波效果。

如上图所示,实现代码中 σ \sigma σ=3,几乎看不出噪声点,并且高斯滤波器模板尺寸越大, 滤波效果越好。当 σ \sigma σ比较大时,二元高斯曲面分布将呈现矮胖型,分布曲面的斜率平缓,数据变化小,高斯滤波模板中系数相差较小。可以近似看作是均值滤波。
中值滤波器
前面大概讨论了均值滤波和高斯滤波的原理、基本实现,但是上述两种滤波方法都存在图像模糊的效应(特别是图像边缘模糊):主要是因为图像的每个像素点灰度值是采用邻域像素点灰度值加权平均的方式进行计算,减小了图像的梯度变化,导致了边缘模糊,同时加和求解的方式将噪声也计算在内,像素点失去原有的灰度值。
均值滤波和高斯滤波都属于线性滤波,而中值滤波属于非线性滤波。中值滤波器在对邻域像素点灰度值统计排序的基础上,使用中位数的灰度值代替图像像素点的灰度值。噪声一般为椒盐噪声,灰度值为0或255,而在邻域像素点的灰度值排序中,最小可能灰度值为0(胡椒噪声),最大可能灰度值为255(白盐噪声),中位数极大可能不是噪声,但也可能是噪声(这种情况如何解决后面会有讲到),这样的话就在很大程度上去除了噪声,同时其图像模糊程度也要比线性滤波器低,具有一种优秀的去噪能力。因此,中值滤波器比均值滤波器更适合用来去除椒盐噪声。
实现代码:
def median_blur(noise_img, size):
result = np.zeros_like(noise_img) # 创建一个零矩阵,用于存储滤波后的图像
padding_img = cv.copyMakeBorder(noise_img,
size[0] // 2, size[0] // 2, size[0] // 2, size[0] // 2,
borderType=cv.BORDER_CONSTANT, value=0)#zero padding操作,保持输出图像尺寸不变
for i in range(noise_img.shape[0]):
for j in range(noise_img.shape[1]):
m = i + (size[0] // 2)
n = j + (size[1] // 2)
a = padding_img[m - (size[0] // 2): m + (size[0] // 2 + 1),
n - (size[0] // 2): n + (size[0] // 2 + 1)]#size邻域内的像素值矩阵
b = np.median(np.ravel(a))#将邻域像素矩阵打平成list,np.median求取中位数
result[i, j] = b
return result
对比线性滤波器的效果,中值滤波器确实能较好地去除噪声,极大程度地降低了图像模糊度(较前面的线性滤波器而言)
[1]数字图像处理:第3版/(美)冈萨雷斯(Gonzalez,R.C),(美)伍兹(Woods, R.E.)著.阮秋琦等译
[2]综述:图像滤波常用算法实现及原理解析
[Until:2021年1月26日,晴转阴,只求勿忘初心,步步向前]