PyTorch教程（8）损失函数(一)

机器学习（深度学习），我们的主要目标是最小化由损失函数定义的误差。每种算法都有不同的误差测量方法。选择合适的损失函数很重要，因为它影响算法尽快生成最佳结果的能力。
损失函数大致可分为两类:分类损失和回归损失。

回归函数预测数量，分类函数预测标签。

回归损失

MSE损失，L2损失

均方损失(Mean Square Error, MSE)是最常用的回归损失函数。MSE是我们的目标变量与预测值之间欧几里得距离的平方和。
$$MSE=\frac{{\sum }_{i=1}^n(y_i-y_i^p{)}^2}{n}$$
其中$n$表示样本数目，$y_i^p$表示第$i$个样本的预测结果，$y_i$表示第$i$个样本的真实结果。
均方误差被用作评估大多数回归算法性能的默认度量标准。

1. 解释
   预测值和实际值之差的平方意味着我们放大了损失。模型惩罚大的误差，而鼓励小的误差。
2. 何时使用
   a. 回归问题
   b. 数值特征不大
   c.问题的维度不是很高

MSE的唯一问题是损失的阶数大于数据的阶数。由于我的数据是1阶的，损失函数MSE的阶为2，所以我们不能直接把数据和损失联系起来。因此，我们取MSE的平方根，即均方根误差RMSE:
$$RMSE=\sqrt{\frac{{\sum }_{i=1}^n(y_i-y_i^p{)}^2}{n}}$$
其中$n$表示样本数目，$y_i^p$表示第$i$个样本的预测结果，$y_i$表示第$i$个样本的真实结果。
这里，我们没有改变损失函数，解还是一样的。我们所做的只是通过开根号来降低损失函数的阶数。

import numpy as np
y_hat = np.array([0.020, 0.176, 0.313])
y_true = np.array([0.019, 0.234, 0.918])
def rmse(predictions, targets):
    differences = predictions - targets
    differences_squared = differences ** 2
    mean_of_differences_squared = differences_squared.mean()
    rmse_val = np.sqrt(mean_of_differences_squared)
    return rmse_val
print("d is: " + str(["%.4f" % elem for elem in y_hat]))
print("p is: " + str(["%.4f" % elem for elem in y_true]))
rmse_val = rmse(y_hat, y_true)
print("rmse error is: " + str(rmse_val))

MAE损失，L1损失

MAE损失就是预测值与真实值之间绝对误差的平均值。可以更好的反映预测误差的实际情况。
$$RMAE=\frac{{\sum }_{i=1}^n|y_i-y_i^p|}{n}$$

1. 解释
   它测量估计值与实际值之间的数值距离。它是误差度量的最简单形式。取误差的绝对值，因为如果不取，负号会抵消正号。这对我们没有用处，反而使它更不可靠。
   MAE值越低，模型越好。我们不能期望它的值为零，因为它可能没有实际用处。这导致了资源的浪费。例如，如果我们的模型的损失在5%以内，那么它在实践中是可以的，使它更精确可能并不真正实用。

2. 何时使用
   a. 回归问题
   b. 简单的模型
   c. 由于神经网络通常用于复杂的问题，这个函数很少被使用。

这个函数有什么潜在的问题吗?嗯,是的。这个损失函数在0处是不可微的。损失函数图为:

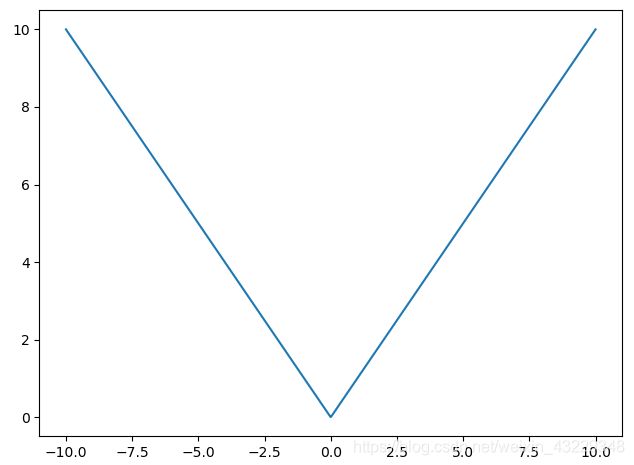
导数在0处不存在。我们需要对函数求导，使其等于0来找到最优点。而在这里是不可能的，我们无法解出这个解。

import numpy as np
y_hat = np.array([0.020, 0.176, 0.313])
y_true = np.array([0.019, 0.234, 0.918])
def mae(true, pred):
	return np.abs(true-pred).mean()
print("d is: " + str(["%.4f" % elem for elem in y_hat]))
print("p is: " + str(["%.4f" % elem for elem in y_true]))
mae_val = mae(y_true, y_hat)
print("mae error is: " + str(mae_val))

Huber 损失

Huber损失结合了MSE和MAE (Mean Absolute Error)的优点:损失小时，梯度小；损失大时，梯度为1。对于较小的误差，它是二次的，否则是线性的(梯度也是类似的)。公式如下:
$L_{\delta }(y,f(x))=\{\begin{array}{cc}\frac{1}{2}(y-f(x){)}^2& \mid y-f(x)\mid \le \delta \\ \delta \mid y-f(x)\mid -\frac{1}{2}{\delta }^2& \text{otherwise}\end{array}$

1. 解释
   如果绝对误差低于$\delta$，它使用平方项，否则使用绝对项。它对异常值的敏感性低于均方误差损失，在某些情况下可以防止梯度爆炸。在均方误差损失中，我们将差进行平方，从而得到一个比原始数字大得多的数字。这些大的数值导致梯度爆炸。对于大于$\delta$的数，这些数不是平方的。
2. 何时使用
   a. 回归问题
   b.当特征值较大时
   c.适合大多数问题

与MSE相比，Huber损失对数据中的异常值更不敏感或更稳健。它在0处也是可微的。它基本上是绝对误差，当误差很小时，它就变成二次误差。误差有多小才能使它成为二次函数取决于一个超参数(delta)，这个超参数是可以调整的。Huber损失在~ 0时接近MAE，在~∞时接近MSE(大数)。

import numpy as np
y_hat = np.array([0.020, 0.176, 0.313])
y_true = np.array([0.019, 0.234, 0.918])
# huber 损失
def huber(true, pred, delta=1):
    loss = np.where(np.abs(true-pred) < delta , 0.5*((true-pred)**2), delta*np.abs(true - pred) - 0.5*(delta**2))
    return loss.mean()
print("d is: " + str(["%.4f" % elem for elem in y_hat]))
print("p is: " + str(["%.4f" % elem for elem in y_true]))
huber_val = huber(y_true, y_hat)
print("huber error is: " + str(huber_val))

$SmoothL1$ 损失函数可以看作超参数$\delta =1$ 的Huber函数。

Log-Cosh损失函数

$$L=\sum _{i=1}^{n}log(cosh(y_i-y_i^p))$$
图形为：

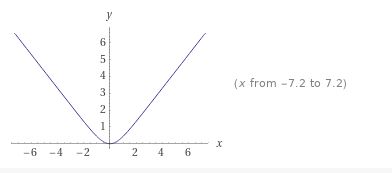
导数为：

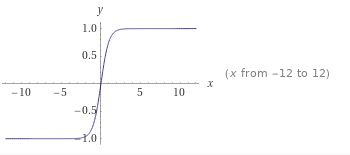
对于较小的误差$\mid y-f(x)\mid$ ，其近似于$MSE$，收敛下降较快；对于较大的误差$\mid y-f(x)\mid$ 其近似等于$\mid y-f(x)\mid -log(2)$ ,类似于$MAE$，不会受到离群点的影响。 Log-Cosh具有Huber损失的所有优点，且不需要设定超参数。相比Huber，Log-Cosh求导比较复杂，计算量较大，在深度学习中使用不多。

分类损失

BCE损失（Binary Crossentropy）

BCE损失常用于二分类任务。如果使用BCE损失函数，则每一个输出节点将数据分类为两个类别。输出值应该通过一个sigmoid激活函数传递，并且输出范围是(0 - 1)。
$$BCELoss=\sum _{i=1}^n(-y_i\ast log{y}_i-(1-y_i)\ast log(1-y_i))$$

在Keras中，如果你没有在最后一层使用sigmoid激活函数会怎样?然后，您可以将from_logits=true作为参数传递给loss函数，它将在内部将sigmoid应用到输出值。

import numpy as np
y_hat = np.array([0.920, 0.976, 0.003])
y_true = np.array([0, 0, 1])

def sigmoid(x):
    return 1. / (1. + np.exp(-x))

def binary_crossentropy(target, output, from_logits=False):
    if not from_logits:
    	# 如果from_logits为False，则将output转换成经过激活函数之前的数值
        output = np.clip(output, 1e-7, 1 - 1e-7)
        output = np.log(output / (1 - output))
    return (target * -np.log(sigmoid(output)) +
            (1 - target) * -np.log(1 - sigmoid(output))).mean()

bce_val = binary_crossentropy(y_true, y_hat)
print("bce error is: " + str(bce_val))

CC损失（Categorical Crossentropy）

多分类交叉熵损失函数，在使用这个loss前面不需要加softmax层。这里GT（或者说target）类型为torch.LongTensor。
$$CELoss=-\frac{1}{N}\sum _{i=1}^N\sum _{k=0}^K{y}_k\ast log{p}_k$$

import numpy as np
y_hat = np.array([[0.920, 0.080], [0.020, 0.80]])
y_true = np.array([[1,0], [0,1]])
def softmax(x, axis=-1):
    y = np.exp(x - np.max(x, axis, keepdims=True))
    return y / np.sum(y, axis, keepdims=True)
def categorical_crossentropy(target, output, from_logits=False):
    if from_logits:
        output = softmax(output)
    else:
        output /= output.sum(axis=-1, keepdims=True)
    output = np.clip(output, 1e-7, 1 - 1e-7)
    return np.sum(target * -np.log(output), axis=-1, keepdims=False)
ce_val = categorical_crossentropy(y_true, y_hat)
print("ce error is: " + str(ce_val))


# 计算topk
def in_top_k(predictions, targets, k):
    top_k = np.argsort(-predictions)[:, :k]
    targets = targets.reshape(-1, 1)
    return np.any(targets == top_k, axis=-1)

Focal Loss损失

Focal Loss解决了什么问题？
（1）难易样本不均衡
（2）类别不均衡

Focal loss的数学定义如下：
$$FL(p_t)=-{\alpha }_t(1-p_t{)}^{\gamma }log(p_t)$$
其中，$\gamma$控制曲线的形状，$\gamma$的值越大越好，好分类样本的loss就越小，我们就可以把模型的注意力投向那些难分类的样本。一个大的$\gamma$让获得小loss的样本范围扩大了。$p_t$的形式如下：
$$p_t=\{\begin{array}{ll}p& \text{if y=1}\\ 1-p& \text{otherwise}\end{array}$$
同时，当$\gamma =0$时，这个表达式就退化成了CrossEntropyLoss:
$$CE(p,y)=\{\begin{array}{ll}-log(p)& \text{if y=1}\\ -log(1-p)& \text{otherwise}\end{array}$$
将上述两个式子合并， CrossEntropyLoss其实就变成了下式：
$$CE(p_t)=-log(p_t)$$

那么$\alpha$是干嘛的呢？解决类别不平衡问题。给稀有类别大的权重，给常见类别小的权重。
$${\alpha }_t=\{\begin{array}{ll}\alpha & \text{if y=1}\\ 1-\alpha & \text{otherwise}\end{array}$$
加上$\alpha$后，交叉熵损失就变成了：
$$CE(p_t)=-{\alpha }_{t}log(p_t)$$
类间不平衡会导致，易分类样本的损失占整个损失的绝大部分，主导了反向传播中的梯度。尽管$\alpha$解决了类别不平衡问题，但是并未区分简单困难样本。
最终将$\alpha$与$\gamma$加入交叉熵损失中后，得到：
$$FL(p_t)=-{\alpha }_t(1-p_t{)}^{\gamma }log(p_t)$$
这样（1）通过$\gamma$解决难易样本不均衡（2）通过$\alpha$解决类别不均衡。
基于alpha=1采用不同的$\gamma$值进行实验的结果：

1. 下面代码实现$\alpha$与$\gamma$作用后的权重

import numpy as np
alpha=0.25
y_true=np.array([1,0,1,0])
y_pred=np.array([0.95,0.05,0.5,0.5])
alpha_weights=[alpha if y==1 else 1-alpha for y in y_true]
print(alpha_weights)

pt=np.zeros(4)
index1=np.argwhere(y_true==1)
index0=np.argwhere(y_true==0)
gama=2
pt[index1]=(1-y_pred[index1])**gama
pt[index0]=(y_pred[index0])**gama
weights=pt*alpha_weights
print(weights)
# [0.25, 0.75, 0.25, 0.75]
# [0.000625 0.001875 0.0625   0.1875  ]

2. 使用PyTorch实现FocalLoss

#!/usr/bin/python3
# -*- encoding: utf-8 -*-
import torchvision
import torch
import numpy as np
import random
from torch import nn
import torch.nn.functional as F


# version 1: use torch.autograd
class FocalLossV1(nn.Module):

    def __init__(self,
                 alpha=0.25,
                 gamma=2,
                 reduction='mean', ):
        super(FocalLossV1, self).__init__()
        self.alpha = alpha
        self.gamma = gamma
        self.reduction = reduction
        self.crit = nn.BCEWithLogitsLoss(reduction='none')

    def forward(self, logits, label):
        '''
        Usage is same as nn.BCEWithLogits:
            >>> criteria = FocalLossV1()
            >>> logits = torch.randn(8, 19, 384, 384)
            >>> lbs = torch.randint(0, 2, (8, 19, 384, 384)).float()
            >>> loss = criteria(logits, lbs)
        '''
        probs = torch.sigmoid(logits)
        coeff = torch.abs(label - probs).pow(self.gamma).neg()
        log_probs = torch.where(logits >= 0,
                                F.softplus(logits, -1, 50),
                                logits - F.softplus(logits, 1, 50))
        log_1_probs = torch.where(logits >= 0,
                                  -logits + F.softplus(logits, -1, 50),
                                  -F.softplus(logits, 1, 50))
        loss = label * self.alpha * log_probs + (1. - label) * (1. - self.alpha) * log_1_probs
        loss = loss * coeff

        if self.reduction == 'mean':
            loss = loss.mean()
        if self.reduction == 'sum':
            loss = loss.sum()
        return loss


class FocalLossV2(nn.Module):
    def __init__(self, alpha=0.25, gamma=2, logits=True, reduce=True):
        super(FocalLossV2, self).__init__()
        self.alpha = alpha
        self.gamma = gamma
        self.logits = logits
        self.reduce = reduce

    def forward(self, inputs, targets):
        if self.logits:
            BCE_loss = F.binary_cross_entropy_with_logits(inputs, targets, reduce=False)
        else:
            BCE_loss = F.binary_cross_entropy(inputs, targets, reduce=False)
        pt = torch.exp(-BCE_loss)
        F_loss = self.alpha * (1 - pt) ** self.gamma * BCE_loss

        if self.reduce:
            return torch.mean(F_loss)
        else:
            return F_loss


if __name__ == '__main__':

    torch.manual_seed(15)
    random.seed(15)
    np.random.seed(15)
    torch.backends.cudnn.deterministic = True


    class Model(nn.Module):
        def __init__(self):
            super(Model, self).__init__()
            net = torchvision.models.resnet18(pretrained=False)
            self.conv1 = net.conv1
            self.bn1 = net.bn1
            self.maxpool = net.maxpool
            self.relu = net.relu
            self.layer1 = net.layer1
            self.layer2 = net.layer2
            self.layer3 = net.layer3
            self.layer4 = net.layer4
            self.out = nn.Conv2d(512, 3, 3, 1, 1)

        def forward(self, x):
            feat = self.conv1(x)
            feat = self.bn1(feat)
            feat = self.relu(feat)
            feat = self.maxpool(feat)
            feat = self.layer1(feat)
            feat = self.layer2(feat)
            feat = self.layer3(feat)
            feat = self.layer4(feat)
            feat = self.out(feat)
            out = F.interpolate(feat, x.size()[2:], mode='bilinear', align_corners=True)
            return out


    net1 = Model()
    net2 = Model()
    net2.load_state_dict(net1.state_dict())

    criteria1 = FocalLossV1()
    criteria2 = FocalLossV2()
    net1.cuda()
    net2.cuda()
    net1.train()
    net2.train()
    net1.double()
    net2.double()
    criteria1.cuda()
    criteria2.cuda()

    optim1 = torch.optim.SGD(net1.parameters(), lr=1e-2)
    optim2 = torch.optim.SGD(net2.parameters(), lr=1e-2)

    bs = 8
    for it in range(100):
        inten = torch.randn(bs, 3, 224, 244).cuda()
        #  lbs = torch.randint(0, 2, (bs, 3, 224, 244)).float().cuda()
        lbs = torch.randn(bs, 3, 224, 244).sigmoid().cuda()
        inten = inten.double()
        lbs = lbs.double()
        logits = net1(inten)
        loss1 = criteria1(logits, lbs)
        optim1.zero_grad()
        loss1.backward()
        optim1.step()
        logits = net2(inten)
        loss2 = criteria2(logits, lbs)
        optim2.zero_grad()
        loss2.backward()
        optim2.step()
        with torch.no_grad():
            if (it + 1) % 10 == 0:
                print('iter: {}, ================='.format(it + 1))
                print('out.weight: ', torch.mean(torch.abs(net1.out.weight - net2.out.weight)).item())
                print('conv1.weight: ', torch.mean(torch.abs(net1.conv1.weight - net2.conv1.weight)).item())
                print('loss: ', loss1.item() - loss2.item())
# iter: 50, =================
# out.weight:  6.965654308057432e-05
# conv1.weight:  1.4111844398871394e-05
# loss:  -0.028864373712213898
# iter: 100, =================
# out.weight:  7.100098406253386e-05
# conv1.weight:  1.8790390456606346e-05
# loss:  -0.028888490619682003

3. 使用Keras实现FocalLoss

import os
from random import shuffle

import cv2
import keras
import matplotlib.pyplot as plt
import numpy as np
import scipy.signal
import tensorflow as tf
from keras.applications.imagenet_utils import preprocess_input
from PIL import Image
def focal(alpha=0.25, gamma=2.0):
    def _focal(y_true, y_pred):
        #---------------------------------------------------#
        #   y_true [batch_size, num_anchor, num_classes+1]
        #   y_pred [batch_size, num_anchor, num_classes]
        #---------------------------------------------------#
        labels         = y_true[:, :, :-1]
        #---------------------------------------------------#
        #   -1 是需要忽略的, 0 是背景, 1 是存在目标
        #---------------------------------------------------#
        anchor_state   = y_true[:, :, -1]  
        classification = y_pred

        # 找出存在目标的先验框
        indices_for_object        = tf.where(keras.backend.equal(anchor_state, 1))
        labels_for_object         = tf.gather_nd(labels, indices_for_object)
        classification_for_object = tf.gather_nd(classification, indices_for_object)

        # 计算每一个先验框应该有的权重
        alpha_factor_for_object = keras.backend.ones_like(labels_for_object) * alpha
        alpha_factor_for_object = tf.where(keras.backend.equal(labels_for_object, 1), alpha_factor_for_object, 1 - alpha_factor_for_object)
        focal_weight_for_object = tf.where(keras.backend.equal(labels_for_object, 1), 1 - classification_for_object, classification_for_object)
        focal_weight_for_object = alpha_factor_for_object * focal_weight_for_object ** gamma

        # 将权重乘上所求得的交叉熵
        cls_loss_for_object = focal_weight_for_object * keras.backend.binary_crossentropy(labels_for_object, classification_for_object)

        # 找出实际上为背景的先验框
        indices_for_back        = tf.where(keras.backend.equal(anchor_state, 0))
        labels_for_back         = tf.gather_nd(labels, indices_for_back)
        classification_for_back = tf.gather_nd(classification, indices_for_back)

        # 计算每一个先验框应该有的权重
        alpha_factor_for_back = keras.backend.ones_like(labels_for_back) * (1 - alpha)
        focal_weight_for_back = classification_for_back
        focal_weight_for_back = alpha_factor_for_back * focal_weight_for_back ** gamma

        # 将权重乘上所求得的交叉熵
        cls_loss_for_back = focal_weight_for_back * keras.backend.binary_crossentropy(labels_for_back, classification_for_back)

        # 标准化，实际上是正样本的数量
        normalizer = tf.where(keras.backend.equal(anchor_state, 1))
        normalizer = keras.backend.cast(keras.backend.shape(normalizer)[0], keras.backend.floatx())
        normalizer = keras.backend.maximum(keras.backend.cast_to_floatx(1.0), normalizer)

        # 将所获得的loss除上正样本的数量
        cls_loss_for_object = keras.backend.sum(cls_loss_for_object)
        cls_loss_for_back = keras.backend.sum(cls_loss_for_back)
        loss = (cls_loss_for_object + cls_loss_for_back) / normalizer
        return loss
    return _focal

参考目录

https://heartbeat.fritz.ai/5-regression-loss-functions-all-machine-learners-should-know-4fb140e9d4b0
https://towardsdatascience.com/https-medium-com-chayankathuria-regression-why-mean-square-error-a8cad2a1c96f
https://blog.csdn.net/weixin_44791964/article/details/102853782
https://github.com/CoinCheung/pytorch-loss/blob/master/focal_loss.py
https://cloud.tencent.com/developer/article/1669261
https://github.com/CoinCheung/pytorch-loss