Eigen库：（二）密集线性问题和分解

1. 线性代数和分解

1.1 线性方程组求解

求解线性方程组Ax=b，b可以是向量，也可以是矩阵。

#include 
#include 
 
using namespace std;
using namespace Eigen;
 
int main()
{
   Matrix3f A;
   Vector3f b;
   A << 1,2,3,  4,5,6,  7,8,10;
   b << 3, 3, 4;
   cout << "Here is the matrix A:\n" << A << endl;
   cout << "Here is the vector b:\n" << b << endl;
   Vector3f x = A.colPivHouseholderQr().solve(b);
   cout << "The solution is:\n" << x << endl;
}

上面的例子是列主元的QR分解，速度很快，是求解线性方程组的一个很折中的选择。colPivHouseholderQr()返回的是A的ColPivHouseholderQR对象，完成对A的QR分解，然后solve()方法返回Ax=b的一个解，如果解存在的话。上面倒数第二句可以用下面两句来代替：

ColPivHouseholderQR<Matrix3f> dec(A);
Vector3f x = dec.solve(b);

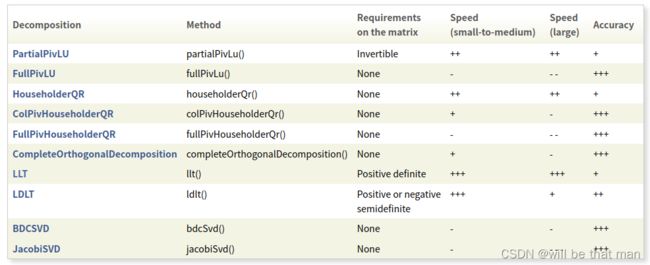
下面给出各种分解的表：

1.2 检查相对误差

#include 
#include 
 
using namespace std;
using namespace Eigen;
 
int main()
{
   MatrixXd A = MatrixXd::Random(100,100);
   MatrixXd b = MatrixXd::Random(100,50);
   MatrixXd x = A.fullPivLu().solve(b);
   double relative_error = (A*x - b).norm() / b.norm(); // norm() is L2 norm
   cout << "The relative error is:\n" << relative_error << endl;
}

1.3 特征值和特征向量

SelfAdjointEigenSolver类是自伴随矩阵的特征分解类，可以用于对一般矩阵和复数矩阵的特征分解。

EigenSolver类是一般矩阵的特征分解类。

ComplexEigenSolver是复数矩阵的特征分解类。

因此SelfAdjointEigenSolver类是包含了EigenSolver和ComplexEigenSolver的所有功能。

#include 
#include 
 
using namespace std;
using namespace Eigen;
 
int main()
{
   Matrix2f A;
   A << 1, 2, 2, 3;
   cout << "Here is the matrix A:\n" << A << endl;
   SelfAdjointEigenSolver<Matrix2f> eigensolver(A);
   if (eigensolver.info() != Success) abort(); // info()检查特征分解是否收敛，一般收敛
   cout << "The eigenvalues of A are:\n" << eigensolver.eigenvalues() << endl;
   cout << "Here's a matrix whose columns are eigenvectors of A \n"
        << "corresponding to these eigenvalues:\n"
        << eigensolver.eigenvectors() << endl;
}

1.4 矩阵的逆和行列式

求矩阵的逆运算比较复杂，一般我们在求解线性方程组都是用矩阵分解solve()来做，因为更加高效。下面给出矩阵求逆和行列式的方法。

A.determinant()
A.inverse()

1.5 最小二乘解

最精确的最小二乘求解方法是SVD分解，还有其他的方法，第二章会说。Eigen提供了两种实现：

• BDCSVD类（推荐），适用于大问题，在较小问题上自动回退到JacobiSVD类。
• JacobiSVD类，适用于小问题。

#include 
#include 
 
using namespace std;
using namespace Eigen;
 
int main()
{
   MatrixXf A = MatrixXf::Random(3, 2);
   cout << "Here is the matrix A:\n" << A << endl;
   VectorXf b = VectorXf::Random(3);
   cout << "Here is the right hand side b:\n" << b << endl;
   cout << "The least-squares solution is:\n"
        << A.bdcSvd(ComputeThinU | ComputeThinV).solve(b) << endl;
}

上述的bdcSvd()内的参数不清楚有什么用，但我们需要指定，可选参数为ComputeFullU, ComputeThinU, ComputeFullV, ComputeThinV。

1.6 利用构造器来分解计算

所有的分解都有一个默认构造器，我们对构造器模板指定数据类型后，就可以利用构造器的compute()方法进行分解，利用solve()方法求解。这样能够避免对象的重新创建。

#include 
#include 
 
using namespace std;
using namespace Eigen;
 
int main()
{
   Matrix2f A, b;
   LLT<Matrix2f> llt;
   A << 2, -1, -1, 3;
   b << 1, 2, 3, 1;
   cout << "Here is the matrix A:\n" << A << endl;
   cout << "Here is the right hand side b:\n" << b << endl;
   cout << "Computing LLT decomposition..." << endl;
   llt.compute(A);
   cout << "The solution is:\n" << llt.solve(b) << endl;
   A(1,1)++;
   cout << "The matrix A is now:\n" << A << endl;
   cout << "Computing LLT decomposition..." << endl;
   llt.compute(A);
   cout << "The solution is now:\n" << llt.solve(b) << endl;
}

我们还可以在创建构造器对象时指定矩阵的大小，这样，对同样大小的矩阵时，就不需要再进行动态内存分配了，节省计算资源。

HouseholderQR<MatrixXf> qr(50,50);
MatrixXf A = MatrixXf::Random(50,50);
qr.compute(A); // no dynamic memory allocation

1.7 秩揭示分解

有些方法是提供了计算秩的方法和计算零空间和列空间的方法。

#include 
#include 
 
using namespace std;
using namespace Eigen;
 
int main()
{
   Matrix3f A;
   A << 1, 2, 5,
        2, 1, 4,
        3, 0, 3;
   cout << "Here is the matrix A:\n" << A << endl;
   FullPivLU<Matrix3f> lu_decomp(A);
   cout << "The rank of A is " << lu_decomp.rank() << endl;
   cout << "Here is a matrix whose columns form a basis of the null-space of A:\n"
        << lu_decomp.kernel() << endl;
   cout << "Here is a matrix whose columns form a basis of the column-space of A:\n"
        << lu_decomp.image(A) << endl; // yes, have to pass the original A
}

2. 线性最小二乘问题

一个过定方程组，比如Ax = b，没有解。在这种情况下，寻找最接近解的向量x是有意义的，即Ax - b的差值尽可能小。这个x称为最小二乘解(如果使用欧几里德范数)。

下面提供三种方法：

• SVD分解：最准确但最慢
• 正规方程：最快但最不准确
• QR分解：两者之间

2.1 SVD分解

#include 
#include 
 
using namespace std;
using namespace Eigen;
 
int main()
{
   MatrixXf A = MatrixXf::Random(3, 2);
   cout << "Here is the matrix A:\n" << A << endl;
   VectorXf b = VectorXf::Random(3);
   cout << "Here is the right hand side b:\n" << b << endl;
   cout << "The least-squares solution is:\n"
        << A.bdcSvd(ComputeThinU | ComputeThinV).solve(b) << endl;
}

2.2 QR分解

QR分解有三个类：

• HouseholderQR (no pivoting, so fast but unstable)
• ColPivHouseholderQR (column pivoting, thus a bit slower but more accurate)
• FullPivHouseholderQR (full pivoting, so slowest and most stable).

MatrixXf A = MatrixXf::Random(3, 2);
VectorXf b = VectorXf::Random(3);
cout << "The solution using the QR decomposition is:\n"
     << A.colPivHouseholderQr().solve(b) << endl;

2.3 正规方程

基于正规方程：

$$A^{T}Ax=A^{T}b$$

MatrixXf A = MatrixXf::Random(3, 2);
VectorXf b = VectorXf::Random(3);
cout << "The solution using normal equations is:\n"
     << (A.transpose() * A).ldlt().solve(A.transpose() * b) << endl;