高斯过程回归(Gaussian Processes Regression, GPR)简介
高斯过程回归(Gaussian Processes Regression, GPR)简介
-
- 一、高斯过程简介
- 二、高斯分布
-
- 1. 一元高斯分布
- 2. 多元高斯分布
- 三、高斯过程回归
-
- 1. 高斯过程
- 2.高斯过程回归
- 四、sklearn中高斯过程回归的使用
-
- 1. 核函数的选择
- 2. sklearn中高斯过程回归的使用
-
- a. 初始数据
- b. 高斯过程回归拟合
- c. 高斯过程回归后验结果分布
- d. 不同核函数拟合结果对比
一、高斯过程简介
高斯过程是一种常用的监督学习方法,可以用于解决回归和分类问题。
高斯过程模型的优点有:
- 预测对观察结果进行了插值
- 预测的结果是概率形式的
- 通用性:可以指定不同的核函数(kernels)形式
高斯过程模型的确定包括:
- 它们不是稀疏的,即它们使用整个样本/特征信息来执行预测
- 高维空间模型会失效,高维也就是指特征的数量超过几十个
值得注意的是,高斯过程模型的优势主要体现在处理非线性和小数据问题上。
参考资料:https://scikit-learn.org/stable/modules/gaussian_process.html
二、高斯分布
1. 一元高斯分布
若一个随机变量 X X X服从均值为 μ \mu μ,方差为 σ 2 \sigma ^2 σ2的高斯分布,则将其写作 X ∼ N ( μ , σ ) X \sim N(\mu, \sigma) X∼N(μ,σ),其概率密度函数形式为:
f ( x ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 f(x) = \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x)=σ2π1e−2σ2(x−μ)2
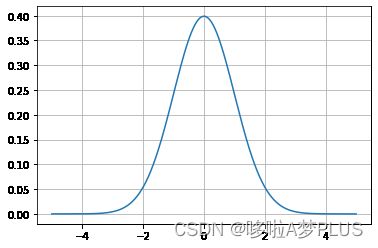
对于均值为0,方差为1的高斯分布可以画出其函数图像:
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(-5, 5, 10000)
y = 1.0/np.sqrt(2.0*np.pi)*np.exp(-1.0*np.power(x, 2)/2.0)
plt.plot(x, y)
plt.grid()
2. 多元高斯分布
对于任意维度的随机变量 X ( x 1 , x 2 , ⋯ , x n ) X(x_1, x_2, \cdots, x_n) X(x1,x2,⋯,xn),其高斯分布可以写作 X ∼ N ( μ , ∑ ) X\sim N(\mu, \sum) X∼N(μ,∑),其中 ∑ \sum ∑为协方差矩阵,其概率密度函数形式为:
f ( X ) = 1 ( 2 π ) n ∣ ∑ ∣ e − 1 2 ( X − μ ) T ∑ − 1 ( X − μ ) f(X) = \frac{1}{\sqrt{(2\pi)^n|\sum|}}e^{-\frac{1}{2}(X-\mu)^T\sum ^{-1}(X-\mu)} f(X)=(2π)n∣∑∣1e−21(X−μ)T∑−1(X−μ)
其中协方差矩阵的形式为:
[ σ ( x 1 , x 1 ) ⋯ σ ( x 1 , x n ) ⋮ ⋱ ⋮ σ ( x n , x 1 ) ⋯ σ ( x n , x n ) ] \begin{bmatrix} \sigma(x_1, x_1) & \cdots & \sigma(x_1,x_n) \\ \vdots & \ddots & \vdots \\ \sigma(x_n, x_1) & \cdots & \sigma(x_n, x_n) \end{bmatrix} ⎣ ⎡σ(x1,x1)⋮σ(xn,x1)⋯⋱⋯σ(x1,xn)⋮σ(xn,xn)⎦ ⎤
其中
σ ( x i , x j ) = ∑ k = 1 c ( x i k − x i ˉ ) ( x j k − x j ˉ ) c − 1 \sigma(x_i, x_j) = \frac{\sum^{c}_{k=1}(x_i^k-\bar{x_i})(x_j^{k}-\bar{x_j})}{c-1} σ(xi,xj)=c−1∑k=1c(xik−xiˉ)(xjk−xjˉ)
其中c代表样本总数,协方差矩阵反映了不同变量之间的相关性大小,如果各个变量之间不相关,那么该矩阵为单位阵。关于多元高斯分布的一个重要性质就是:多元高斯分布的条件分布同样符合高斯分布。
参考资料:https://zhuanlan.zhihu.com/p/518236536
三、高斯过程回归
顾名思义,高斯过程回归就是通过高斯过程来求解回归问题,回归是指通过适当的建模来拟合一组自变量 X X X和因变量 y y y之间的函数关系,建模的方式有很多种,最常用的有线性回归,多项式回归等,高斯过程是其中的一种。
1. 高斯过程
将多元高斯分布推广到连续域上的无限维高斯分布,就得到了高斯过程。如下图所示,在时域 T T T上,对于每一时刻 t i t_i ti,相应的表观值都服从高斯分布,即是 t i ∼ N ( μ i , σ i ) t_i \sim N(\mu _i, \sigma _i) ti∼N(μi,σi),那么对于整个时域 T T T上的联合分布,满足多元高斯分布,即是
T ( t 1 , t 2 , ⋯ , t n ) ∼ N ( μ ( t ) , ∑ ( t i , t j ) ) T(t_1, t_2, \cdots,t_n)\sim N(\mu(t), \sum(t_i, t_j)) T(t1,t2,⋯,tn)∼N(μ(t),∑(ti,tj))
其中每个时刻的均值用一个均值函数刻画,两个不同时刻之间的相关性用一个协方差函数刻画。
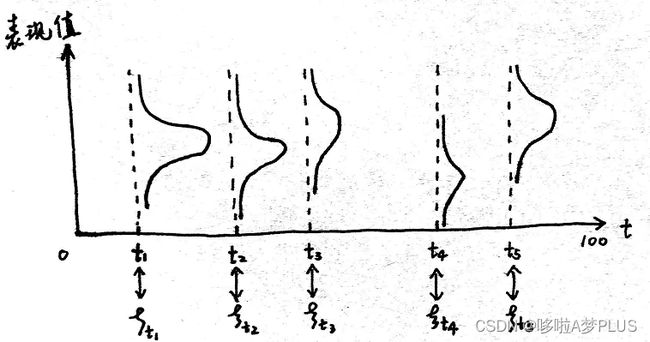
因此我们只需要两个因素来确定一个高斯过程:
- 均值函数
- 协方差函数(矩阵)
2.高斯过程回归
高斯过程回归的是通过有限的高维数据来拟合出相应的高斯过程,从而来预测任意随机变量下的函数值。具体而言,对于一组随机变量 X 1 , X 2 , ⋯ , X n X_1, X_2, \cdots, X_n X1,X2,⋯,Xn和目标值 y 1 , y 2 , ⋯ y n y_1, y_2, \cdots y_n y1,y2,⋯yn,我们假设其服从多元高斯分布,即是:
[ X 1 , X 2 , ⋯ , X n ] ∼ N ( y 1 , y 2 , ⋯ , y n , ∑ ) [X_1, X_2, \cdots, X_n]\sim N(y_1, y_2, \cdots, y_n,\sum) [X1,X2,⋯,Xn]∼N(y1,y2,⋯,yn,∑)
这其中的问题是需要确定协方差矩阵,它反映了不同采样点之间的相似性大小,合法的协方差矩阵要求是半正定的,因此这里我们需要指定相应的核函数来度量这一相似性,sklearn中提供了很多的核函数,后面介绍。确定了协方差矩阵之后,我们就能根据已有的数据确定变量空间中的无限维高斯分布,并且相应地能够确定任意采样点处的条件高斯分布,即是相应的概率分布,如下图所示:
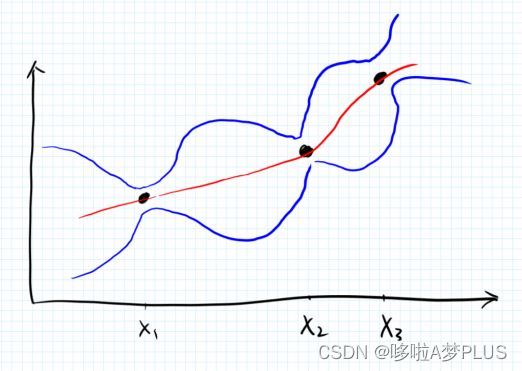
具体推到过程参考以下三篇文章。
- 浅谈高斯回归
- 高斯过程 Gaussian Processes 原理、可视化及代码实现
- 快速入门高斯过程(Gaussian process)回归预测
四、sklearn中高斯过程回归的使用
1. 核函数的选择
前面已经说明,核函数的作用是描述不同采样点之间的相似性大小,sklearn中内置了很多核函数,如下图所示:
|
Kernel which is composed of a set of other kernels. |
|
Constant kernel. |
|
Dot-Product kernel. |
|
Exp-Sine-Squared kernel (aka periodic kernel). |
|
The Exponentiation kernel takes one base kernel and a scalar parameter p and combines them via |
|
A kernel hyperparameter's specification in form of a namedtuple. |
|
Base class for all kernels. |
|
Matern kernel. |
|
Wrapper for kernels in sklearn.metrics.pairwise. |
|
The |
|
Radial basis function kernel (aka squared-exponential kernel). |
|
Rational Quadratic kernel. |
|
The |
|
White kernel. |
除了sklearn中提供的核函数之外,也可以自定义核函数。
2. sklearn中高斯过程回归的使用
a. 初始数据
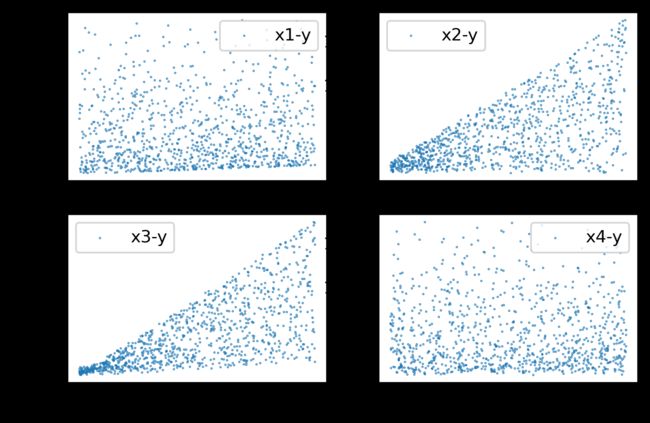
这里我们利用 sklearn.datasets.make_friedman2 生成初始数据,friedman2 生成输入数据是一个 n_sample x 4维的矩阵,下面是其调用及可视化。
from sklearn.datasets import make_friedman2
import matplotlib.pyplot as plt
X, y = make_friedman2(n_samples=1000, noise=0.1, random_state=10)
plt.figure(dpi=300)
ax1 = plt.subplot(221)
ax1.scatter(X[:, 0], y, label='x1-y', s=0.1)
ax1.legend()
ax1 = plt.subplot(222)
ax1.scatter(X[:, 1], y, label='x2-y', s=0.1)
ax1.legend()
ax1 = plt.subplot(223)
ax1.scatter(X[:, 2], y, label='x3-y', s=0.1)
ax1.legend()
ax1 = plt.subplot(224)
ax1.scatter(X[:, 3], y, label='x4-y', s=0.1)
ax1.legend()
b. 高斯过程回归拟合
from sklearn.datasets import make_friedman2
from sklearn.model_selection import train_test_split
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, Sum, WhiteKernel
import matplotlib.pyplot as plt
X, y = make_friedman2(n_samples=1000, noise=0.1, random_state=10)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=36)
model_kernel = Sum(RBF([100, 1500, 1, 10], length_scale_bounds='fixed'), WhiteKernel(0.1, noise_level_bounds='fixed'))
model_gpr = GaussianProcessRegressor(kernel=model_kernel)
model_gpr.fit(X_train, y_train)
print(model_gpr.score(X_test, y_test))
y_mean, y_std = model_gpr.predict(X_test, return_std=True)
plot_x = [i for i in range(X_test.shape[0])]
plt.figure(dpi=300)
plt.scatter(plot_x, y_test, color='red', label='test data')
plt.plot(plot_x, y_mean, color='blue', label='y predict')
plt.legend()

这里使用的是RBF和白噪声核函数,根据 x 1 , x 2 , x 3 , x 4 x_1,x_2,x_3,x_4 x1,x2,x3,x4四个特征大小选取了不同大小的长度缩放尺度,拟合得到的模型较好,评分为0.99。
c. 高斯过程回归后验结果分布
from sklearn.datasets import make_friedman2
from sklearn.model_selection import train_test_split
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import DotProduct, RBF, Sum, Matern, PairwiseKernel
import matplotlib.pyplot as plt
import numpy as np
x_train = np.random.uniform(0, 5, 6).reshape(-1, 1)
y_train = np.sin(np.power(x_train-2.5, 2))
model_kernel = RBF(length_scale=1.0, length_scale_bounds=(1e-1, 10.0))
model_gpr = GaussianProcessRegressor(kernel=model_kernel)
model_gpr.fit(x_train, y_train)
plot_x = np.linspace(0, 5, 10000).reshape(-1, 1)
y_mean, y_std = model_gpr.predict(plot_x, return_std=True)
plt.figure(dpi=300)
plt.xlim([0, 5.0])
plt.ylim([-2.0, 2.0])
plt.scatter(x_train, y_train, label="train")
plt.plot(plot_x[:, 0], y_mean, '--', label='predict y')
plt.fill_between(plot_x[:, 0], y_mean-y_std, y_mean+y_std, color='black', alpha=0.1, label=r"predict y $\pm$ std")
plt.legend()
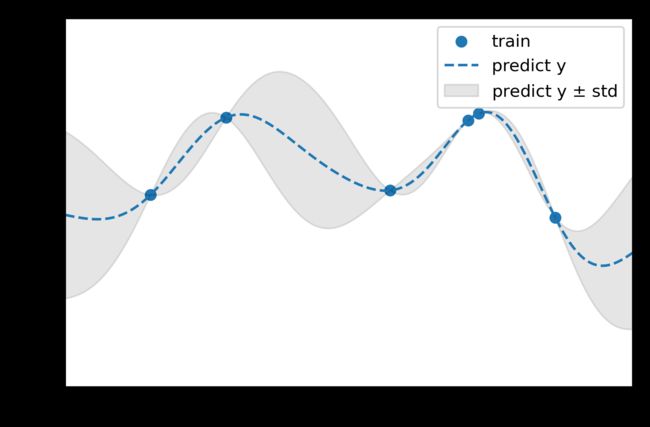
如上图为高斯过程回归拟合得到模型的预测值,可以看到结果是概率分布,灰色区域为95%置信区间。
d. 不同核函数拟合结果对比
对于以上c中的数据,这里用了四种不同的核函数来拟合,如下为代码和拟合结果。
from sklearn.datasets import make_friedman2
from sklearn.model_selection import train_test_split
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import DotProduct, RBF, Matern, PairwiseKernel
import matplotlib.pyplot as plt
import numpy as np
x_train = np.random.uniform(0, 5, 10).reshape(-1, 1)
y_train = np.sin(np.power(x_train-2.5, 2))
model_k1 = DotProduct(sigma_0=1, sigma_0_bounds=(1e-1, 10.0))
model_k2 = RBF(length_scale=1.0, length_scale_bounds=(1e-1, 10.0))
model_k3 = Matern(length_scale=1.0, length_scale_bounds=(1e-1, 10.0), nu=1.5)
model_k4 = PairwiseKernel(gamma=1.0, gamma_bounds=(1e-1, 10), metric='poly')
plt.figure(dpi=300)
plt.xlim([0, 5.0])
plt.ylim([-2.0, 2.0])
plt.scatter(x_train, y_train, label="train")
plot_x = np.linspace(0, 5, 10000).reshape(-1, 1)
for model_kernel in [model_k1, model_k2, model_k3, model_k4]:
model_gpr = GaussianProcessRegressor(kernel=model_kernel)
model_gpr.fit(x_train, y_train)
y_mean = model_gpr.predict(plot_x)
plt.plot(plot_x[:, 0], y_mean, '--', color=(np.random.random(), np.random.random(), np.random.random()), label='kernels: {}'.format(model_kernel.__str__()))
plt.legend()