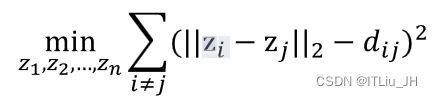数据分析-降维-PCA-LDA-LLE

目录

前言

矩阵分解法

主成分分析（PCA）

核PCA 

非负矩阵分解（NMF）

FactorAnalysis

独立主成分分析（ICA）

判别分析法（LDA）

基于流形学习的数据降维方法

LLE

 MDS

 MDS实现

t-SNE

---

前言

降维指采用某种映射方法，将高维空间中的数据点映射到低维度的空间中。降维的本质是学习一个映射函数 f : w->v，其中w是原始数据点的表达，目前最多使用向量表达形式。 v是数据点映射后的低维向量表达，通常v的维度小于w的维度。
原始数据在采集时可能包含了很高的维度，降维可以降低时间复杂度和空间复杂度，节省了开销；去掉数据集中夹杂的噪声，提高模型的泛化性能；降维使得模型具有更强的鲁棒性；也可以更好的解释数据，更好的可视化。

Sklearn中降维的方法主要分布在以下三个模块：
sklearn.decomposition：包含了绝大部分的矩阵分解算法，其中包括PCA、核PCA、NMF或ICA等
decomposition.PCA    主成分分析（PCA）
decomposition.NMF    非负矩阵分解（NMF）
decomposition.FastICA    独立主成分分析（ICA）
decomposition.FactorAnalysis    因子分析
decomposition.KernelPCA    核PCA

sklearn.discriminant_analysis：包含了LDA和QDA两种判别分析方法
discriminant_analysis.LinearDiscriminantAnalysis    线性判别分析（LDA）
discriminant_analysis.QuadraticDiscriminantAnalysis    二次判别分析（QDA）（非降维）

sklearn.manifold：包含了基于流形学习的数据降维方法等
manifold.LocallyLinearEmbedding    局部线性嵌入（LLE）
manifold.MDS    多维尺度变换（MDS）
manifold.TSNE    t分布随机邻域嵌入（t-SNE）
manifold.Isomap    等度量映射（Isomap）

矩阵分解法

主成分分析（PCA）

构造原始特征的一系列线性组合形成低维的特征，以去除数据的相关性，并使降维后的数据最大程度地保持原始高维数据的方差信息。

如下图，将二维空间的点变到一维空间。

 

 实现 decomposition.PCA    

# PCA降维
from sklearn.decomposition import PCA
pca = PCA(n_components=5)
# 训练集训练
pca.fit(X_train)
# 训练集降维
X_train_pca = pca.transform(X_train)
## 测试集降维
X_test_pca = pca.transform(X_test)
# 查看方差贡献率
print(sum(pca.explained_variance_ratio_))
# 查看方差贡献值
print(sum(pca.explained_variance_))

核PCA 

Non-linear dimensionality reduction through the use of kernels

对于输入空间(Input space)中的矩阵X，我们先用一个非线性映射（由核函数确定）把X中的所有样本映射到一个高维甚至是无穷维的空间(称为特征空间，Feature space)，使其线性可分，然后在这个高维空间进行PCA降维。

实现 decomposition.KernelPCA    

from sklearn.decomposition import KernelPCA
kpca = KernelPCA(n_components=3,kernel="sigmoid",random_state=10)
X_kpca = kpca.fit_transform(X)

'''
KernelPCA(
    n_components=None,
    *,
    kernel='linear',
    gamma=None,
    degree=3,
    coef0=1,
    kernel_params=None,
    alpha=1.0,
    fit_inverse_transform=False,
    eigen_solver='auto',
    tol=0,
    max_iter=None,
    remove_zero_eig=False,
    random_state=None,
    copy_X=True,
    n_jobs=None,
)
'''

非负矩阵分解（NMF）

decomposition.NMF    

非负矩阵分解(Non-negative Matrix Factorization)

一种主成分分析的方法，要求数据和成分都要非负，对图像数据十分有效

NMF希望找到两个矩阵和，使得与原数据的误差尽可能的少，即：

​

其中表示Frobenius范数，X代表N×p的数据矩阵，W是N×r的基矩阵， 是r×p的权重矩阵， r≤max⁡(N,p)，其中X，W和H都是非负矩阵

 加入正则化项，

其中，α为1与2正则化项的参数，而1正则化项占总正则化项的比例。

加入正则化项后，常用的拟牛顿法和梯度下降法并不适用，Sklearn中采用坐标轴下降法进行优化。

nmf = NMF(n_components=6, init='nndsvda', random_state=10)
nmf.fit(faces)
faces_nmf = nmf.components_

# 还原图像
plot_gallery("NMF Faces", faces_nmf[:6])

FactorAnalysis

A simple linear generative model with Gaussian latent variables.

The observations are assumed to be caused by a linear transformation of
lower dimensional latent factors and added Gaussian noise.
Without loss of generality the factors are distributed according to a
Gaussian with zero mean and unit covariance. The noise is also zero mean
and has an arbitrary diagonal covariance matrix.

from sklearn.decomposition import FactorAnalysis
Fa = FactorAnalysis(n_components=3,random_state=0)
Fa.fit_transform(X)
'''
FactorAnalysis(
    n_components=None,
    *,
    tol=0.01,
    copy=True,
    max_iter=1000,
    noise_variance_init=None,
    svd_method='randomized',
    iterated_power=3,
    rotation=None,
    random_state=0,
)
'''

独立主成分分析（ICA）

ICA认为观测信号是若干个统计独立的分量的线性组合，ICA要做的是一个解混过程。而PCA是一个信息提取的过程，将原始数据降维，目前已成为ICA将数据标准化的预处理步骤。

FastICA：a fast algorithm for Independent Component Analysis.

from sklearn.decomposition import FastICA
ica = FastICA(n_components=3, random_state=10)
X_pca = ica.fit_transform(X)
'''
FastICA(
    n_components=None,
    *,
    algorithm='parallel',
    whiten=True,
    fun='logcosh',
    fun_args=None,
    max_iter=200,
    tol=0.0001,
    w_init=None,
    random_state=None,
)
'''

判别分析法（LDA）

线性判别分析（Linear Discriminant Analysis, LDA）是一种典型的有监督线性降维方法。

LDA的目标是利用样本的类别标签信息，找到一个利于数据分类的线性低维表示。

这个目标可以从两个角度来量化

第一个角度是使得降维后相同类样本尽可能近，使用类内离散度 (within-class scatter)度量

第二个角度是使得降维后不同类样本尽可能远，使用类间离散度 (between-class scatter)度量

下图展示原始样本分为两类并用不同图形表示

利用PCA方法，将得到直线，可见降维后的两类数据无法很好区分

利用LDA方法，能够找到直线，使得降维后两类数据很好地被区分开

​

 ​

 实现

# 训练模型并评估模型
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda = LinearDiscriminantAnalysis(n_components=2)
lda.fit(X_train, y_train)
y_pred = lda.predict(X_test)
lda.score(X_test, y_test)
# 输出方差贡献率
print(sum(lda.explained_variance_ratio_))

基于流形学习的数据降维方法

LLE

流形：一个低维空间在一个高维空间中被扭曲之后的结果，低维流形嵌入在高维空间中

形象解释：“二维平面的一块布，把它扭一扭在三维空间中就变成了一个流形”

样本在高维空间分布复杂，但在局部上具有欧式空间的性质

在局部建立降维映射关系，再由局部推广到全局

数据被降至2维或3维，方便进行可视化

将数据降到低维空间中，但是保留数据局部的线性关系

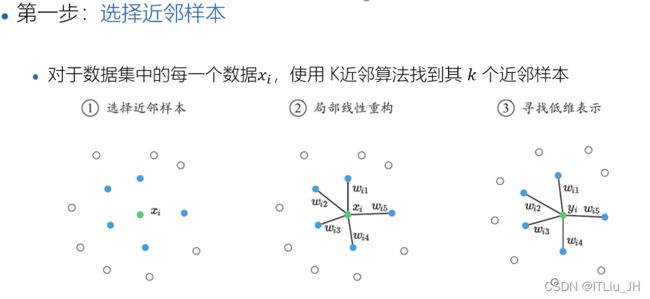
每一个样本点可以写成其 个近邻点的线性组合，从高维嵌入（embedding）到低维时尽量保持局部的线性关系

​

 ​

 ​

 LLE实现

from sklearn.manifold import LocallyLinearEmbedding
# 设置不同近邻数
n_neighbors = [5, 10, 15, 20, 50, 80] 
# 降至2维
n_components = 2
fig = plt.figure(figsize=(20, 8))
for i, number in enumerate(n_neighbors):
    # LLE进行降维
    Y = LocallyLinearEmbedding(n_neighbors=number, n_components=n_components, random_state=10).fit_transform(X)
    # 绘图
    ax = fig.add_subplot(231 + i)
    plt.scatter(Y[:, 0], Y[:, 1], c=color, cmap=plt.cm.Spectral)
    plt.title("n_neighbors = %s" % (number))

# 设置不同的算法
methods = ['standard', 'ltsa', 'hessian', 'modified']
fig = plt.figure(figsize=(20, 5))
for i, methods in enumerate(methods):
    # LLE进行降维，近邻数固定为50
    Y = LocallyLinearEmbedding(n_neighbors=50, n_components=n_components, method=methods, random_state=10).fit_transform(X)
    # 绘图
    ax = fig.add_subplot(141 + i)
    plt.scatter(Y[:, 0], Y[:, 1], c=color, cmap=plt.cm.Spectral)
    plt.title("method = %s" % (methods))

 MDS

 多维尺度变换(Multi-dimensional Scaling，MDS)的目标是找到数据的低维表示，使得降维前后样本之间的相似度信息尽量得以保留

多维尺度变换能够只利用样本间的距离信息，找到每一个样本的特征表示，且在该特征表示下样本的距离与原始的距离尽量接近

假设数据集包含n个样本，数据集用n×p的矩阵表示，样本i能够使用一个p维的特征向量x_i表示，样本间距离矩阵可以用n×n的矩阵D表示，其元素d_ij表示样本i和样本j的距离假设z_i为样本x_i在低维空间的表示，即样本和样本的欧式距离。

MDS的优化目标为

​

 ​

 ​

 MDS实现

from sklearn.manifold import MDS
## 使用MDS降维并得到降维结果
mds = MDS(n_components, random_state=10)
Y = mds.fit_transform(X)
## 降维可视化
plt.figure(figsize=(8, 6))
plt.scatter(Y[:, 0], Y[:, 1], c=color, cmap=plt.cm.Spectral)
plt.title("MDS") 

t-SNE

t-distributed Stochastic Neighbor Embedding.

t-SNE  is a tool to visualize high-dimensional data. It converts similarities between data points to joint probabilities and tries to minimize the Kullback-Leibler divergence between the joint probabilities

of the low-dimensional embedding and the
high-dimensional data. t-SNE has a cost function that is not convex,
i.e. with different initializations we can get different results.

It is highly recommended to use another dimensionality reduction
method (e.g. PCA for dense data or TruncatedSVD for sparse data)
to reduce the number of dimensions to a reasonable amount (e.g. 50)
if the number of features is very high. This will suppress some
noise and speed up the computation of pairwise distances between
samples. For more tips see Laurens van der Maaten's FAQ [2].

from sklearn.manifold import TSNE
tsne = TSNE(n_components=3,random_state=0)
X_tsne = tsne.fit_transform(X)
'''
TSNE(
    n_components=2,
    *,
    perplexity=30.0,
    early_exaggeration=12.0,
    learning_rate=200.0,
    n_iter=1000,
    n_iter_without_progress=300,
    min_grad_norm=1e-07,
    metric='euclidean',
    init='random',
    verbose=0,
    random_state=None,
    method='barnes_hut',
    angle=0.5,
    n_jobs=None,
    square_distances='legacy',
)

'''

待完善...

参考文献

......