图机器学习(Graph Machine Learning)- 第三章 无监督图学习 (Unsupervised Graph Learning)- 浅嵌入方法
第三章 无监督图学习
文章目录
- 第三章 无监督图学习
- 前言
- 3.1 无监督图嵌入路线图
- 3.2 浅嵌入方法 Shallow embedding methods
-
- 3.2.1 矩阵分解 Matrix factorization
-
- 3.2.1.1 图因子分解 Graph factorization
- 3.2.1.2 高阶邻近保持嵌入 Higher-order proximity preserved embedding, HOPE
- 3.2.1.3 具有全局结构信息的图表示 GraphRep
- 3.2.2 Skip-gram
- 3.2.3 DeepWalk
- 3.2.4 Node2Vec
- 3.2.5 Edge2Vec
- 3.2.6 Graph2Vec
- 小结
前言
无监督机器学习是机器学习算法的一个分支,在训练过程中不利用任何目标信息。相反,他们自己发现聚类,发现模式,发现异常,并解决许多其他问题,这些问题没有老师,也没有已知的先验正确答案。
与其他许多机器学习算法一样,无监督模型在图表示学习领域有大量应用。实际上,它们是解决各种下游任务(如节点分类和社区检测等)的非常有用的工具。
在本章中,我们将概述最近的无监督图嵌入方法。对于一个图,这些技术的目标是自动学习它的潜在表示,其中的关键结构组件以某种方式保留下来。
本章将涉及以下主题:
无监督图嵌入路线图 The unsupervised graph embedding roadmap
浅嵌入方法 Shallow embedding methods
自编码 Autoencoders
图神经网络 Graph neural networks
3.1 无监督图嵌入路线图
图是定义在非欧几里德空间中的复杂数学结构。粗略地说,这意味着定义什么是close什么并不总是容易的;甚至很难说close意味着什么。想象一个社交网络图:两个用户可以分别连接在一起,但却共享非常不同的功能——一个可能对时尚和服装感兴趣,而另一个可能对体育和电子游戏感兴趣。我们能把它们看作是“close”吗?
因此,无监督机器学习算法在图分析中得到了大量应用。无监督机器学习是一类机器学习算法,可以在不需要人工标注数据的情况下进行训练。其中大多数模型确实只利用邻接矩阵和节点特征中的信息,而不需要下游的机器学习任务的知识。
最常用的解决方案之一是学习保持图结构的嵌入。学习后的表示通常是最优的,以便它可以用来重建成对节点的相似性,例如邻接矩阵。这些技术带来了一个重要的特征:学习后的表示可以编码节点或图之间的潜在关系,允许我们发现隐藏的和复杂的新模式。
许多算法都与无监督图机器学习技术相关。然而,正如文献(https://arxiv.org/abs/2005.03675) 所示,这些算法可以分为从宏观上分为:浅嵌入方法、自动编码器和图神经网络 (GNNs),如图3.1所示:

3.2 浅嵌入方法 Shallow embedding methods
正如在第二章图机器学习中已经介绍过的,使用浅嵌入方法,我们确定了一组算法,这些算法能够学习并只返回学习到的输入数据的嵌入值。
在本节中,我们将详细解释其中的一些算法。此外,我们将提供几个例子来丰富描述如何在Python中使用这些算法。对于本节中描述的所有算法,我们将使用以下库来实现:Graph Embedding Methods (GEM),Node to Vector (Node2Vec),Karate Club。
3.2.1 矩阵分解 Matrix factorization
矩阵分解是一种广泛应用于不同领域的通用分解技术。一致数量的图嵌入算法使用这种技术来计算一个图的节点嵌入。
我们将从介绍矩阵分解问题开始。在介绍了基本原理之后,我们将描述两种算法,即图因子分解(Graph Factorization (GF)) 与高阶邻近保持嵌入(Higher-Order Proximity Preserved Embedding(HOPE)) 方法,利用矩阵分解来构建图的节点嵌入。
令 W ∈ R m × n W \in \mathbb{R}^{m \times n} W∈Rm×n为输入数据,矩阵因子分解将 W W W近似分解为 W ≈ V × H W \approx V \times H W≈V×H, 其中$V \in \mathbb{R}^{m \times d} 和 和 和H \in \mathbb{R}^{d \times n}$ 分别为源矩阵(source) 和丰度(abundance) 矩阵, d d d为生成嵌入空间的维数。矩阵分解算法通过最小化损失函数来学习 V V V和 H H H矩阵,该损失函数可以根据我们想要解决的具体问题而改变。在其一般公式中,损失函数是通过使用Frobenius范数 ∣ ∣ W − V × H ∣ ∣ F 2 ||W-V \times H||_F^2 ∣∣W−V×H∣∣F2计算重构误差来定义的.
一般来说,所有基于矩阵分解的无监督嵌入算法都使用相同的原理。它们都将一个表示为不同分量的矩阵的输入图进行因式分解。每种方法之间的主要区别在于优化过程中使用的损失函数。实际上,不同的损失函数允许创建一个强调输入图形特定属性的嵌入空间。
3.2.1.1 图因子分解 Graph factorization
GF算法是计算图的节点嵌入的模型之一。根据我们前面描述的矩阵分解原理,GF算法分解给定图的邻接矩阵。
从形式上来看,设 G = ( V , E ) G=(V,E) G=(V,E)是我们要计算节点嵌入的图, A ∈ R ∣ V ∣ × ∣ V ∣ A∈\mathbb{R}^{| V|×|V |} A∈R∣V∣×∣V∣是其邻接矩阵。该矩阵分解问题中使用的损失函数为:
L = 1 2 ∑ ( i , j ) ∈ E ( A i , j − Y i , : Y j , : T ) 2 + λ 2 ∑ i ∣ ∣ Y i , : ∣ ∣ 2 L = \frac{1}{2} \sum_{(i,j)\in E}(A_{i,j}-Y_{i,:}Y_{j,:}^T)^2 + \frac{\lambda}{2} \sum_{i} ||Y_{i,:}||^2 L=21(i,j)∈E∑(Ai,j−Yi,:Yj,:T)2+2λi∑∣∣Yi,:∣∣2
上式中 ( i , j ) ∈ E (i,j)\in E (i,j)∈E表示 G G G中的一条边, Y ∈ R ∣ V ∣ × d Y∈\mathbb{R}^{| V|×d} Y∈R∣V∣×d是包含 d d d维嵌入的矩阵。矩阵的每一行表示给定节点的内嵌。此外,嵌入矩阵的正则项确保问题在缺乏足够数据的情况下仍然是适定的。
该方法中使用的损失函数主要是为了提高GF的性能和可扩展性。实际上,这种方法生成的解可能是有噪声的。此外,通过观察矩阵分解公式可以看出GF执行了一个强对称分解。这个特性特别适用于无向图,其中邻接矩阵是对称的,但可能是有向图的一个潜在限制。
在下面的代码中,我们将展示如何使用Python和GEM库执行给定networkx图的节点嵌入:
import matplotlib.pyplot as plt
#定义画图函数
def draw_graph(G, node_names={}, node_size=500):
pos_nodes = nx.spring_layout(G)
nx.draw(G, pos_nodes, with_labels=True, node_size=node_size, edge_color='gray', arrowsize=30)
pos_attrs = {}
for node, coords in pos_nodes.items():
pos_attrs[node] = (coords[0], coords[1] + 0.08)
#nx.draw_networkx_labels(G, pos_attrs, font_family='serif', font_size=20)
plt.axis('off')
axis = plt.gca()
axis.set_xlim([1.2*x for x in axis.get_xlim()])
axis.set_ylim([1.2*y for y in axis.get_ylim()])
plt.show()
from pathlib import Path
Path("gem/intermediate").mkdir(parents=True, exist_ok=True) #生成路径
# 首次使用需安装gem 模块 pip install git+https://github.com/palash1992/GEM.git
from gem.embedding.gf import GraphFactorization
G = nx.barbell_graph(m1=10, m2=4) #生成一个哑铃图,包含2个size=10的完全图和一个长度为4的路径
draw_graph(G)
gf = GraphFactorization(d=2, data_set=None,max_iter=10000, eta=1*10**-4, regu=1.0) #生成一个d=2维的嵌入空间
gf.learn_embedding(G) #计算输入图G的节点嵌入
(array([[ 0.005649 , -0.00162848],
[ 0.00564943, -0.00162778],
[ 0.00565073, -0.00162701],
[ 0.00564531, -0.0016282 ],
[ 0.00567283, -0.00160997],
[ 0.00569636, -0.00177473],
[ 0.00534768, -0.0017131 ],
[ 0.00712381, -0.00220416],
[ 0.00325992, -0.00191946],
[ 0.00836498, 0.00132794],
[ 0.00664959, -0.00526292],
[ 0.00277289, -0.0031307 ],
[-0.00731414, 0.00334539],
[-0.00501265, 0.00347537],
[-0.00066064, 0.00035803],
[-0.00066021, 0.0003574 ],
[-0.00066684, 0.00036028],
[-0.00065625, 0.00036165],
[-0.0006718 , 0.0003454 ],
[-0.00074331, 0.00036039],
[-0.00055733, 0.00053317],
[-0.00108717, 0.0004539 ],
[ 0.00249238, -0.00077529],
[-0.00636049, 0.0006267 ]]),
8.368745803833008)
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10,10))
for x in G.nodes():
v = gf.get_embedding()[x] #提取计算的嵌入
ax.scatter(v[0],v[1], s=1000) #显示为散点图
ax.annotate(str(x), (v[0],v[1]), fontsize=12)
- 利用
networkx生成一个杠铃图(G),用作GF分解算法的输入。 - 利用
GraphFactorization类生成一个d=2维的嵌入空间。 - 使用
gf.learn_embedding(G)计算输入图的节点嵌入。 - 通过调用
gf.get_embedding()方法提取计算得到的嵌入。
从结果可以看到,属于组1和组3的节点是如何映射到同一个空间区域中的。这些点由属于第2组的节点分隔。这种映射使我们能够很好地将第1组和第3组与第2组分开。但不幸的是,第1组和第3组之间没有明确的区分。
3.2.1.2 高阶邻近保持嵌入 Higher-order proximity preserved embedding, HOPE
HOPE是另一种基于矩阵分解原理的图嵌入技术。该方法允许保持高阶邻近性,且不强制其嵌入具有任何对称性质。在开始描述这个方法之前,我们先来了解一下一阶邻近和高阶邻近的含义:
- 一阶邻近(First-order proximity):给定图 G = ( V , E ) G=(V,E) G=(V,E),其中边具有权重 W i j W_{ij} Wij,对每个节点对 ( v i , v j ) (v_i,v_j) (vi,vj),若 ( v i , v j ) ∈ E (v_i,v_j) \in E (vi,vj)∈E,则称其一阶邻近等于 W i j W_{ij} Wij,否则,两节点间的一阶邻近为0。
- 二阶和高阶邻近(Second- and high-order proximity): 利用二阶接近性,我们可以表示顶点之对之间的两步关系。 对每个顶点对 ( v i , v j ) (v_i,v_j) (vi,vj),二阶邻近可以看做是从 v i v_i vi到 v j v_j vj的两步转移。高阶邻近性进一步泛化了这一概念,并允许我们表示一个更全局的结构。高阶邻近度可以看作是从从 v i v_i vi到 v j v_j vj的 k k k步 ( k ≥ 3 ) (k≥3) (k≥3)过渡。
有了邻近性的定义,下面我们可以来描述HOPE方法。令 G = ( V , E ) G=(V,E) G=(V,E)为需要计算嵌入的图, A ∈ R ∣ V ∣ × ∣ V ∣ A \in \mathbb{R}^{|V|\times |V|} A∈R∣V∣×∣V∣是其邻接矩阵。该问题的损失函数定义如下:
L = ∣ ∣ S − Y s × Y t T ∣ ∣ F 2 L = ||S - Y_s \times Y_t^T||_F^2 L=∣∣S−Ys×YtT∣∣F2
上式中 S ∈ R ∣ V ∣ × ∣ V ∣ S \in \mathbb{R}^{|V|\times |V|} S∈R∣V∣×∣V∣ 是由图 G G G生成的相似度矩阵, Y s ∈ R ∣ V ∣ × d Y_s \in \mathbb{R}^{|V|\times d} Ys∈R∣V∣×d, Y t ∈ R ∣ V ∣ × d Y_t \in \mathbb{R}^{|V|\times d} Yt∈R∣V∣×d是两个在 d d d维嵌入空间中表示的嵌入矩阵。更详细的, Y s Y_s Ys表示源嵌入, Y t Y_t Yt表示目标嵌入。
HOPE利用这两个矩阵来捕捉有向网络中的非对称邻近性,其中方向从源节点指向目标节点。最终的嵌入矩阵 Y Y Y是通过简单地将 Y s Y_s Ys和 Y t Y_t Yt矩阵按列连接而得到的。因此HOPE最终产生的嵌入空间将会有 2 ∗ d 2∗d 2∗d维。
正如我们前面提及的, S S S矩阵是原始图 G G G的相似度矩阵。 S S S 的目标是获得高阶邻近信息。可由 S = M g ⋅ M l S = M_g \cdot M_l S=Mg⋅Ml得到,其中$ M_g, M_l$均为矩阵多项式。
在原始文献中,HOPE的作者给出了不同的计算$ M_g, M_l 的 方 法 。 这 里 我 们 仅 介 绍 一 种 简 单 的 常 用 计 算 方 法 , ∗ ∗ A d a m i c − A d a r ( A A ) ∗ ∗ 。 这 里 的方法。这里我们仅介绍一种简单的常用计算方法,**Adamic-Adar (AA)** 。这里 的方法。这里我们仅介绍一种简单的常用计算方法,∗∗Adamic−Adar(AA)∗∗。这里 M_g = I$, M l = A ⋅ D ⋅ A M_l = A \cdot D \cdot A Ml=A⋅D⋅A,其中 D = 1 ∑ ( A i j + A j i ) D = \frac{1}{\sum (A_{ij} + A_{ji})} D=∑(Aij+Aji)1为对角矩阵。其他的计算 $ M_g, M_l$的方法还包括Katz Index, Rooted PageRank (RPR), Common Neighbors (CN)。
在下面的代码中,我们将展示如何使用Python和GEM库执行给定networkx图的节点嵌入:
import networkx as nx
from gem.embedding.hope import HOPE
G = nx.barbell_graph(m1=10, m2=4)
draw_graph(G)
hp = HOPE(d=4, beta=0.01)
hp.learn_embedding(G) #利用HOPE将G嵌入到d=4维空间
(array([[ 0.07024409, 0.07024348, 0.07024409, 0.07024348],
[ 0.07024409, 0.07024348, 0.07024409, 0.07024348],
[ 0.07024409, 0.07024348, 0.07024409, 0.07024348],
[ 0.07024409, 0.07024348, 0.07024409, 0.07024348],
[ 0.07024409, 0.07024348, 0.07024409, 0.07024348],
[ 0.07024409, 0.07024348, 0.07024409, 0.07024348],
[ 0.07024409, 0.07024348, 0.07024409, 0.07024348],
[ 0.07024409, 0.07024348, 0.07024409, 0.07024348],
[ 0.07024409, 0.07024348, 0.07024409, 0.07024348],
[ 0.07104037, 0.07104201, 0.07104037, 0.07104201],
[ 0.00797181, 0.00799433, 0.00797181, 0.00799433],
[ 0.00079628, 0.00099787, 0.00079628, 0.00099787],
[-0.00079628, 0.00099787, -0.00079628, 0.00099787],
[-0.00797181, 0.00799433, -0.00797181, 0.00799433],
[-0.07104037, 0.07104201, -0.07104037, 0.07104201],
[-0.07024409, 0.07024348, -0.07024409, 0.07024348],
[-0.07024409, 0.07024348, -0.07024409, 0.07024348],
[-0.07024409, 0.07024348, -0.07024409, 0.07024348],
[-0.07024409, 0.07024348, -0.07024409, 0.07024348],
[-0.07024409, 0.07024348, -0.07024409, 0.07024348],
[-0.07024409, 0.07024348, -0.07024409, 0.07024348],
[-0.07024409, 0.07024348, -0.07024409, 0.07024348],
[-0.07024409, 0.07024348, -0.07024409, 0.07024348],
[-0.07024409, 0.07024348, -0.07024409, 0.07024348]]),
0.04996991157531738)
#画嵌入散点图
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10,10))
for x in G.nodes():
#由于原始图是无向图,因此源节点和目标节点没有区别,取嵌入矩阵的前两列画散点图
v = hp.get_embedding()[x,2:]
ax.scatter(v[0],v[1], s=1000)
ax.annotate(str(x), (v[0],v[1]), fontsize=20)

在上例中,由于原始图是无向图,因此源节点和目标节点没有区别,嵌入矩阵的前两列表示 。从图中也可以看出HOPE生成的嵌入空间在本例中可以更好地分离不同的节点。
3.2.1.3 具有全局结构信息的图表示 GraphRep
具有全局结构信息的图表示(GraphRep),如HOPE,允许我们保持高阶邻近性,而不强制其嵌入具有对称性。从形式上看,令 G = ( V , E ) G=(V,E) G=(V,E)为需要计算节点嵌入的图, A ∈ R ∣ V ∣ × ∣ V ∣ A \in \mathbb{R}^{|V|\times |V|} A∈R∣V∣×∣V∣是其邻接矩阵。该问题的损失函数定义如下:
L = ∣ ∣ X k − Y s k × Y t k T ∣ ∣ F 2 , 1 ≤ k ≤ K L = ||X^k - Y_s^k \times {Y_t^k}^T||_F^2, 1\leq k \leq K L=∣∣Xk−Ysk×YtkT∣∣F2,1≤k≤K
上式中 X k ∈ R ∣ V ∣ × ∣ V ∣ X^k \in \mathbb{R}^{|V|\times |V|} Xk∈R∣V∣×∣V∣是由图 G G G生成的矩阵,用于得到节点之间的第 k k k阶邻近。 Y s k ∈ R ∣ V ∣ × d Y_s^k \in \mathbb{R}^{|V|\times d} Ysk∈R∣V∣×d, Y t k ∈ R ∣ V ∣ × d Y_t^k \in \mathbb{R}^{|V|\times d} Ytk∈R∣V∣×d是源节点和目标节点在 d d d维嵌入空间中的 k k k阶邻近。 X k = ∏ k ( D − 1 A ) X^k = \prod_{k} (D^{-1}A) Xk=∏k(D−1A). D D D被称为度矩阵,是一个对角矩阵,可通过如下计算得到:
D i j = { ∑ A i p , i = j 0 , i ≠ j D_{ij} = \begin{cases} \sum A_{ip}, & i=j\\ 0,& i \neq j \end{cases} Dij={∑Aip,0,i=ji=j
X 1 = D − 1 A X^1 = D^{-1}A X1=D−1A 表示(一步)概率转移矩阵, X i j 1 X_{ij}^1 Xij1 表示从 v i v_i vi到 v j v_j vj的一步转移概率, X i j k X_{ij}^k Xijk 表示从 v i v_i vi到 v j v_j vj的 k k k步转移概率.
每一阶的邻近都通过一个独立的优化问题计算。然后将生成的所有 k k k个嵌入矩阵按列串联,得到最终的源嵌入矩阵。
在下面的代码中,我们将展示如何使用Python和karatclub库执行给定networkx图的节点嵌入:
import networkx as nx
from karateclub.node_embedding.neighbourhood.grarep import GraRep
G = nx.barbell_graph(m1=10, m2=4)
draw_graph(G)
gr = GraRep(dimensions=2,order=3)
#2维嵌入空间,节点邻近最大阶数为3,最终的嵌入矩阵的列数为dimension*order
gr.fit(G)
embeddings = gr.get_embedding()
embeddings #每个节点的嵌入变量为一个2*3=6维向量
array([[ 13.392852 , 13.408884 , 14.690813 , -14.603628 ,
17.966175 , 13.389623 ],
[ 13.392852 , 13.408884 , 14.690813 , -14.603628 ,
17.966175 , 13.389623 ],
[ 13.392852 , 13.408884 , 14.690813 , -14.603628 ,
17.966175 , 13.389623 ],
[ 13.392852 , 13.408885 , 14.690813 , -14.603628 ,
17.966175 , 13.389623 ],
[ 13.392852 , 13.408884 , 14.690813 , -14.603628 ,
17.966175 , 13.389623 ],
[ 13.392852 , 13.408884 , 14.690813 , -14.60363 ,
17.966175 , 13.389623 ],
[ 13.392852 , 13.408885 , 14.690813 , -14.60363 ,
17.966175 , 13.389623 ],
[ 13.392852 , 13.408885 , 14.690813 , -14.603628 ,
17.966175 , 13.389623 ],
[ 13.392852 , 13.408885 , 14.690813 , -14.603628 ,
17.966177 , 13.389623 ],
[ 11.760014 , 11.578869 , 14.057339 , -10.999479 ,
15.445142 , 11.519671 ],
[ 12.952441 , 12.806962 , 14.31821 , -12.021735 ,
14.415425 , 12.798148 ],
[ 2.184538 , -0.30208588, 15.1362505 , -11.759393 ,
26.771967 , -1.449792 ],
[ 2.1845179 , 0.3022315 , 15.1362295 , 11.759424 ,
26.771975 , 1.4498051 ],
[ 12.953293 , -12.806104 , 14.318185 , 12.021766 ,
14.415431 , -12.798142 ],
[ 11.760778 , -11.578092 , 14.057317 , 10.999511 ,
15.445145 , -11.519667 ],
[ 13.39374 , -13.407992 , 14.690788 , 14.603661 ,
17.966179 , -13.38962 ],
[ 13.39374 , -13.407992 , 14.690788 , 14.603661 ,
17.966179 , -13.389619 ],
[ 13.39374 , -13.407992 , 14.690788 , 14.603661 ,
17.966179 , -13.389619 ],
[ 13.39374 , -13.407992 , 14.690787 , 14.603661 ,
17.966179 , -13.389619 ],
[ 13.39374 , -13.407992 , 14.690787 , 14.6036625 ,
17.966179 , -13.389619 ],
[ 13.39374 , -13.407992 , 14.690787 , 14.6036625 ,
17.966179 , -13.389619 ],
[ 13.39374 , -13.407992 , 14.690787 , 14.6036625 ,
17.966179 , -13.389619 ],
[ 13.39374 , -13.407992 , 14.690787 , 14.6036625 ,
17.96618 , -13.389619 ],
[ 13.39374 , -13.407993 , 14.690787 , 14.603662 ,
17.96618 , -13.389619 ]], dtype=float32)
#由于是2维嵌入空间,因此embeddings[:,:2] 为一阶嵌入,embeddings[:,2:4] 为2阶嵌入,embeddings[:,4:] 为3阶嵌入,
embeddings[:,:2]
array([[ 13.392852 , 13.408884 ],
[ 13.392852 , 13.408884 ],
[ 13.392852 , 13.408884 ],
[ 13.392852 , 13.408885 ],
[ 13.392852 , 13.408884 ],
[ 13.392852 , 13.408884 ],
[ 13.392852 , 13.408885 ],
[ 13.392852 , 13.408885 ],
[ 13.392852 , 13.408885 ],
[ 11.760014 , 11.578869 ],
[ 12.952441 , 12.806962 ],
[ 2.184538 , -0.30208588],
[ 2.1845179 , 0.3022315 ],
[ 12.953293 , -12.806104 ],
[ 11.760778 , -11.578092 ],
[ 13.39374 , -13.407992 ],
[ 13.39374 , -13.407992 ],
[ 13.39374 , -13.407992 ],
[ 13.39374 , -13.407992 ],
[ 13.39374 , -13.407992 ],
[ 13.39374 , -13.407992 ],
[ 13.39374 , -13.407992 ],
[ 13.39374 , -13.407992 ],
[ 13.39374 , -13.407993 ]], dtype=float32)
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10,10))
#1阶嵌入
ida = 0
idb = 1
for x in G.nodes():
v = gr.get_embedding()[x]
ax.scatter(v[ida],v[idb], s=1000)
ax.annotate(str(x), (v[ida],v[idb]), fontsize=12)
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10,10))
#2阶嵌入
ida = 2
idb = 3
for x in G.nodes():
v = gr.get_embedding()[x]
ax.scatter(v[ida],v[idb], s=1000)
ax.annotate(str(x), (v[ida],v[idb]), fontsize=12)
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10,10))
#3阶嵌入
ida = 4
idb = 5
for x in G.nodes():
v = gr.get_embedding()[x]
ax.scatter(v[ida],v[idb], s=1000)
ax.annotate(str(x), (v[ida],v[idb]), fontsize=12)
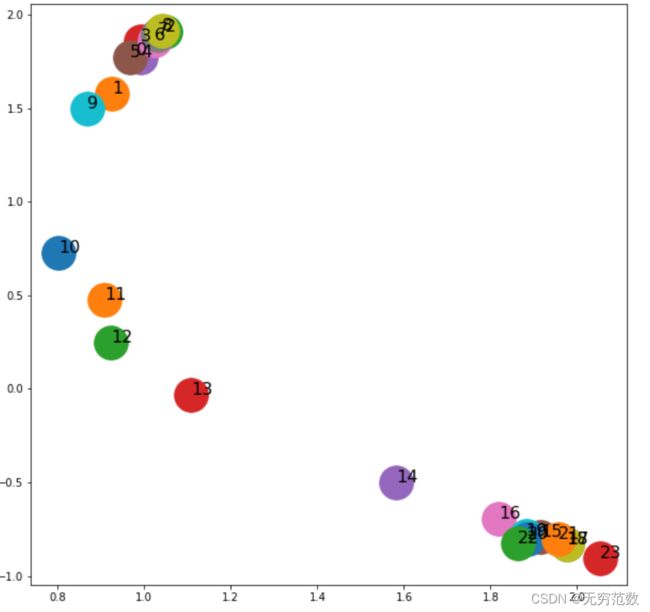
从以上高阶嵌入图中可以看出,我们可以很容易地看出,不同的邻近顺序是如何让我们得到不同的嵌入的。由于输入图非常简单,在这种情况下,在k=1时得到了一个分离良好的嵌入空间。需要指出的是,在组1和组3的节点在所有邻近阶中属于具有相同的嵌入值(它们在散点图中是重叠的)。
在本节中,我们描述了一些用于无监督图嵌入的矩阵分解方法。在下一节中,我们将介绍一种使用skip-gram模型执行无监督图嵌入的不同方法。
3.2.2 Skip-gram
在本节中,我们将简要描述skip-gram模型。由于它被广泛地应用于不同的嵌入算法中,因此需要对其进行高阶的描述以更好地理解不同的方法。在深入详细描述之前,我们将首先给出一个简要的概述。
skip-gram模型是一个简单的神经网络,它有一个隐藏层,用来预测输入词出现时给定词出现的概率。该神经网络的训练是通过使用一个文本语料库作为参考而建立的训练数据。
这个过程如下图所示:

图3.5中描述的例子显示了生成训练数据的算法是如何工作的。选择一个目标单词,并围绕该单词构建一个固定大小w的滚动窗口。滚动窗口内的单词被称为上下文单词。然后根据滚动窗口内的单词构建多个(目标词、上下文词)对。
一旦从整个语料库中生成训练数据,就会训练skip-gram模型来预测一个词成为给定目标上下文词的概率。在训练过程中,神经网络学习输入单词的紧凑表示。这就是为什么skip-gram模型也被称为Word to Vector (Word2Vec) 。
表示skip-gram模型的神经网络结构如下图所示:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-t47uhPN2-1649639617653)(fig3-6.png “skip-gram-NN”)]
神经网络的输入是一个大小为m的二进制向量。向量的每个元素代表我们想要嵌入这些单词的语言字典中的一个单词。在训练过程中,当给定(目标词、上下文词)对时,输入数组中除了表示“目标”词的项等于1外,所有项都为0。隐藏层有d个神经元。隐藏层将学习每个单词的嵌入表示,创建一个d维嵌入空间。
最后,神经网络的输出层是m个神经元(与输入向量大小相同)的稠密层,具有softmax激活函数。每个神经元代表字典中的一个单词。神经元赋予的值对应于该词与输入词“相关”的概率。当m的大小增加时,softmax很难计算,分层softmax方法常被使用。
skip-gram模型的最终目标不是真正学习我们前面描述的任务,而是建立一个输入单词的紧凑的d维表示。由于有了这种表示方式,可以使用隐藏层的权重轻松地提取单词的嵌入空间。另一种创建Skip-gram模型的常见方法是基于上下文的:Continuous Bag-of-Words(CBOW) 。
由于已经介绍了skip-gram模型背后的基本概念,我们可以开始描述一系列建立在该模型上的无监督图嵌入算法。一般来说,所有基于skip-gram模型的无监督嵌入算法都使用相同的原理。
从一个输入图开始,他们从中提取一系列的游走步。这些游走可以看作一个文本语料库,其中每个节点表示一个单词。如果两个单词(表示节点)在游走中由一条边连接,则它们在文本中相邻。每种方法之间的主要区别在于计算这些步数的方式。实际上,正如我们将看到的,不同的游走生成算法可以强调图的特定局部或全局结构。
3.2.3 DeepWalk
DeepWalk算法使用skip-gram模型生成给定图的节点嵌入。为了更好地解释这个模型,我们需要引入随机游走(random walks) 的概念。
形式上,假设 G G G是一个图,选择一个顶点 v i v_i vi作为起始点。我们随机选择一个邻居 v j v_j vj然后向它移动。将从一点出发随机选择另一个点移动这个过程反复进行 t t t次。以这种方式得到的 t t t个顶点的随机序列是一个长度的随机游走。值得一提的是,用于生成随机游动的算法对它们的构建方式没有任何约束。因此,不能保证节点的局部邻域被很好地保存。
利用随机游走的概念,DeepWalk算法为每个节点生成一个最大为t的随机游走。这些随机游走将作为skip-gram模型的输入。使用skip-gram生成的嵌入将被用作最终的节点嵌入。在下图(图3.7)中,我们可以看到算法的分步表示:

下面是对上述图表中描述的算法的一步一步的解释:
-
随机游动生成(Random Walk Generation):对于输入图 G G G的每个节点,计算一组最大长度固定 ( t ) (t) (t)的随机游走。应该注意到长度 t t t是一个上界。不存在强制所有路径具有相同长度的约束。
-
** Skip-Gram 训练:** 使用上一步中生成的所有随机游走,训练一个Skip-Gram模型。如前所述,skip-gram模型适用于单词和句子。当一个图作为skip-gram模型的输入时,如图3.7所示,一个图可以看作是一个输入文本语料库,而图的单个节点可以看作语料库的一个单词。
随机游走可以被看作是一个单词序列(句子)。然后使用随机游走中节点生成的“假”句子训练跳跃图。前面描述的skip-gram模型的参数(窗口大小w和嵌入大小d)将在此步骤中使用。 -
嵌入生成(Embedding Generation):利用训练好的skip-gram模型隐藏层中所包含的信息,提取每个节点的嵌入。
在下面的代码中,我们将展示如何使用Python和karatclub库执行给定networkx图的节点嵌入:
import networkx as nx
from karateclub.node_embedding.neighbourhood.deepwalk import DeepWalk
G = nx.barbell_graph(m1=10, m2=4)
draw_graph(G)
dw = DeepWalk(dimensions=2)
dw.fit(G)
embeddings = dw.get_embedding()
3.2.4 Node2Vec
Node2Vec 算法可以看作是DeepWalk的扩展。与DeepWalkl类似,Node2Vec也生成一组随机游走,用作skip-gram模型的输入。 一旦训练完毕,就使用skip-gram模型的隐藏层来生成在图中嵌入节点。 这两种算法的主要区别在于在随机游走的生成方式。
实际上,DeepWalk不使用偏差生成随机游走,Node2Vec中引入了一种新的技术来在图上生成有偏差的随机游走。生成随机游走的算法结合了宽度优先搜索(Breadth-First Search,BFS) 和深度优先搜索(Depth-First Search,DFS) 的图搜索方法。这两种算法在随机游走生成中的组合方式是通过两个参数 p , q p,q p,q进行正则化的。 p p p定义了随机游走返回到前一个节点的概率, q q q定义了随机游走通过图中之前未见过的部分的概率。
由于以上组合,Node2Vec可以通过保持图中的局部结构和全局社区结构来保持高阶邻近性。这种新的随机游走生成方法可以解决DeepWalk在保持节点的局部邻域特性方面的局限性。
在下面的代码中,我们将展示如何使用Python和node2vec库执行给定networkx图的节点嵌入:
import networkx as nx
from node2vec import Node2Vec
G = nx.barbell_graph(m1=10, m2=4)
draw_graph(G)
node2vec = Node2Vec(G, dimensions=2) # 嵌入空间的维数为2
model = node2vec.fit(window=10) # 对模型进行拟合
embeddings = model.wv # 嵌入

值得注意的是,model.wv是 Word2VecKeyedVectors类的一个对象。
为了得到以nodeid为ID的特定节点的嵌入向量,我们可以使用训练后的模型model.wv[str(nodeid)]。
Node2Vec其他参数如下:
- num_walks:为每个节点生成的随机游走步数
- walk_length:生成的随机游走的长度
- p, q:随机游走生成算法的p和q参数
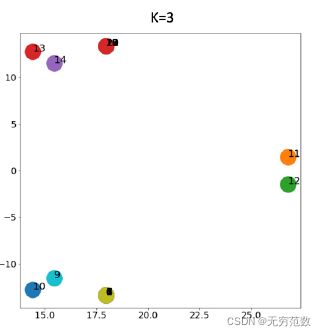
从下图可以看出,与DeepWalk相比,Node2Vec可以让我们在嵌入空间中获得更好的节点分离。区域1和3很好地聚集在两个空间区域中。而区域2正好位于两组的中间,没有任何重叠。
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10,10))
for x in G.nodes():
v = model.wv[str(x)]
ax.scatter(v[0],v[1], s=1000)
ax.annotate(str(x), (v[0],v[1]), fontsize=16)
plt.show()
3.2.5 Edge2Vec
与其他嵌入函数不同,Edge2Vec(Edge to Vector) 算法在边而不是节点上生成嵌入空间。该算法是使用Node2Vec生成的嵌入的一个简单附带作用。其主要思想是利用两个相邻节点的节点嵌入来进行一些基本的数学运算,以提取连接它们的边的嵌入。
形式上,设 v i v_i vi和 v j v_j vj为两个相邻节点, f ( v i ) f(v_i) f(vi)和 f ( v j ) f(v_j) f(vj)为用Node2Vec计算的嵌入值。可以使用表3.1中描述的运算符来计算其边缘的嵌入
在下面的代码中,我们将展示如何使用Python和Node2Vec库执行给定networkx图的节点嵌入:
#HadamardEmbedder类只使用keyed_vectors参数。该参数值为Node2Vec生成的内嵌模型。
from node2vec.edges import HadamardEmbedder
edges_embs = HadamardEmbedder(keyed_vectors=model.wv)
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10,10))
for x in G.edges():
v = edges_embs[(str(x[0]), str(x[1]))]
ax.scatter(v[0],v[1], s=1000)
ax.annotate(str(x), (v[0],v[1]), fontsize=16)
plt.show()
要使用其他方法来生成边缘嵌入,我们只需要从表3.1中列出的类中选择一个即可。
from node2vec.edges import AverageEmbedder
edges_embs = AverageEmbedder(keyed_vectors=model.wv)
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10,10))
for x in G.edges():
v = edges_embs[(str(x[0]), str(x[1]))]
ax.scatter(v[0],v[1], s=1000)
ax.annotate(str(x), (v[0],v[1]), fontsize=16)
plt.show()
from node2vec.edges import WeightedL1Embedder
edges_embs = WeightedL1Embedder(keyed_vectors=model.wv)
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10,10))
for x in G.edges():
v = edges_embs[(str(x[0]), str(x[1]))]
ax.scatter(v[0],v[1], s=1000)
ax.annotate(str(x), (v[0],v[1]), fontsize=16)
plt.show()
from node2vec.edges import WeightedL2Embedder
edges_embs = WeightedL2Embedder(keyed_vectors=model.wv)
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10,10))
for x in G.edges():
v = edges_embs[(str(x[0]), str(x[1]))]
ax.scatter(v[0],v[1], s=1000)
ax.annotate(str(x), (v[0],v[1]), fontsize=16)
plt.show()
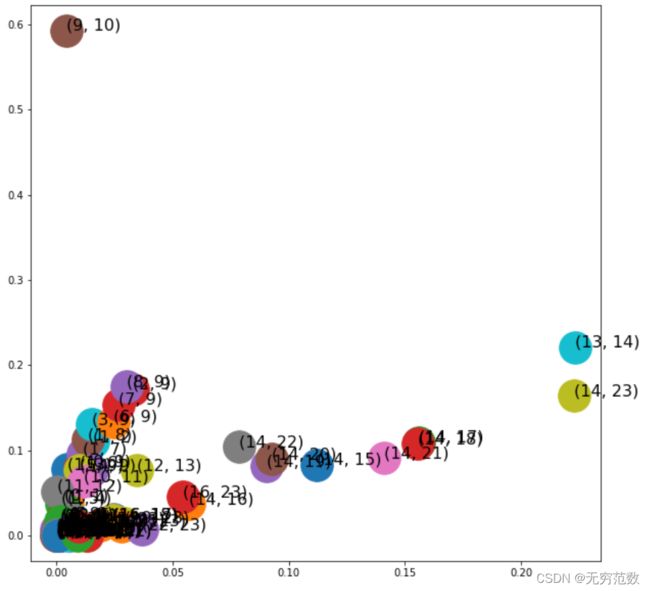
从上图可以看出,不同的嵌入方法是产生完全不同的嵌入空间。在本例中,AverageEmbedder和HadamardEmbedder为区域1、2和3生成分离良好的嵌入。而对于WeightedL1Embedder和WeightedL2Embedder,由于边缘嵌入集中在单个区域,没有显示出清晰的聚类,嵌入空间不能很好地分离。
3.2.6 Graph2Vec
我们前面描述的方法为给定图上的每个节点或边生成嵌入空间。Graph to Vector(Graph2Vec) 概括了这个概念,并为整个图生成嵌入。
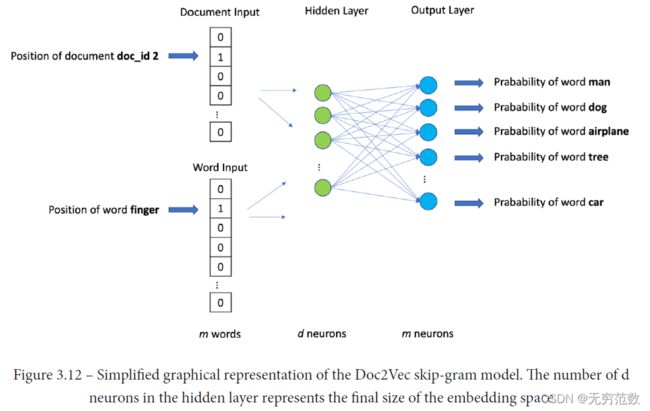
给定的一组图,Graph2Vec算法生成一个嵌入空间,其中每个点代表一个图。该算法被称为Document to Vector (Doc2Vec) ,可看做Word2Vec 和 skip-gram模型的综合。 我们可以在图3.12中直观地看到这个模型的简化:
与简单的Word2Vec相比,Doc2Vec还接受另一个表示包含输入单词的文档的二进制数组。给定一个“目标”文档和一个“目标”单词,模型就会尝试预测与输入的“目标”单词和文档相关的最可能的“上下文”单词。
随着Doc2Vec模型的引入,我们现在可以描述Graph2Vec算法了。这种方法背后的主要思想是将整个图视为一个文档,并将其每个子图视为一个自我图(ego graph)(参见第1章,Getting Started with Graphs),作为组成文档的单词。
换句话说,图由子图组成,就像文档由句子组成一样。根据此描述,该算法可归纳为以下步骤:
- 子图生成:围绕每个节点生成一组有根的子图。
- Doc2Vec训练:使用上一步生成的子图来训练Doc2Vec skip-gram图。
- 嵌入生成:利用经过训练的Doc2Vec模型隐藏层中所包含的信息,提取每个节点的嵌入。
在下面的代码中我们将展示如何使用Python和karatclub库执行一组networkx图的节点嵌入:
import random
import matplotlib.pyplot as plt
from karateclub import Graph2Vec
n_graphs = 20
def generate_radom(): #用随机参数生成了20个Watts-Strogatz图。
n = random.randint(6, 20)
k = random.randint(5, n)
p = random.uniform(0, 1)
return nx.watts_strogatz_graph(n,k,p), [n,k,p]
Gs = [generate_radom() for x in range(n_graphs)]
model = Graph2Vec(dimensions=2, wl_iterations=10) #生成2维嵌入
model.fit([x[0] for x in Gs]) #对输入数据进行模型拟合
embeddings = model.get_embedding() #提取包含嵌入的向量
fig, ax = plt.subplots(figsize=(10,10))
for i,vec in enumerate(embeddings):
ax.scatter(vec[0],vec[1], s=1000)
ax.annotate(str(i), (vec[0],vec[1]), fontsize=40)
小结
在本节中,我们描述了不同的基于矩阵分解和skip-gram模型的浅嵌入方法。然而,目前也存在大量的无监督嵌入算法,如拉普拉斯方法。有兴趣的读者可以参考Machine Learning on Graphs: A Model and Comprehensive Taxonomy https://arxiv.org/pdf/2005.03675.pdf.
在下一节中,我们将继续描述无监督图嵌入方法。我们将描述基于自编码器的更复杂的图嵌入算法。