Python 技巧 —— 矩阵操作
![]()
欢迎关注 “小白玩转Python”,发现更多 “有趣”
使用 NumPy 学习矩阵和求解线性方程组的完整指南
矩阵作为一种数学资源被用于一些现实世界的应用。在本文中,您将使用强大的 NumPy 库学习 Python 中的矩阵,如下所示:
1. 什么是 NumPy,什么时候应该使用它?
2. 使用 NumPy 构造矩阵
3. 矩阵的运算和实例
4. 如何执行矩阵切片
另外:我们还将探讨如何使用 Python 中的矩阵来计算线性方程模型。
让我们从 Python 的矩阵开始。
1. NumPy 是什么,什么时候使用?
NumPy 是一个 Python 库,可以对单个和多维数组和矩阵进行简单的数值计算。顾名思义,NumPy 在数值计算中脱颖而出。许多数据科学库(如 pandas、 scikit-learn 和 SciPy)都依赖 NumPy。它构成了当今 python 编写的数据科学应用程序的一部分。
许多线性代数计算可以很容易地解决 NumPy。在几种机器学习算法中,线性代数是一种重要的数学方法。通过深入了解 NumPy,您可以构建库或扩展现有库以用于机器学习。
提供:
一个强 n 维数组对象,名为ndarray
广播功能
C/C + + 和 Fortran 代码合并工具
生成线性代数,傅里叶变换,和随机数能力
现在让我们进一步了解 Python 矩阵,看看矩阵是如何形成的。
2. 使用 NumPy 构造矩阵
用列表形成一个矩阵
import numpy as np
# Create a 2D numpy array with python lists
new_array = np.array([[ 1, 2, 3],[ 4, 5, 6]])
print(new_array)
输出如下:
[[1 2 3]
[4 5 6]]
结果显示了一个2D 矩阵,其中 np.array()的输入是一个列表[1,2,3] ,[4,5,6]。父列表中的每个列表在矩阵中创建一行。
形成一个具有范围的矩阵
print(np.arange(0,4))
上述声明输出下列一维数组:
[0 1 2 3]
要形成一个2D 矩阵,我们可以在一个列表中使用 np.arange ()。我们将这个列表传递给 np.array () ,它将创建一个2D NumPy 数组。
print(np.array([np.arange(0,4), np.arange(5,9)]))
上面的语句产生以下二维数组:
[[0 1 2 3]
[5 6 7 8]]
NumPy 数组形状
每个 NumPy 对象都是一个 n 维数组。在数学中,它被称为 n 维矩阵。对于它的形式,可以指定任何 numpy ndarray 对象。
# Using example from above p to form a matrix with ranges
new_array_2d = np.array([np.arange(0,4), np.arange(5,9)])
print(new_array_2d.shape)
输出:
(2,4)
上面的输出引用了这样一个事实:矩阵有两行和四列。
由0和1组成的矩阵
由0
# Create a matrix of order(3, 3) filled with zeros
# By default float64 type of numbers are generated if not specified
print(np.zeros((3, 3)))
输出:
[[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]]
由1
print(np.ones((2, 2), dtype=np.int16))
输出:
[[1 1]
[1 1]]
在形成矩阵时,我们传递了一个附加的 dtype = np.int16参数。这需要使用 np.ones 特性而不是默认的 float 来生成整数。您还可以将这个附加参数传递到 np.zeros中。
3. 矩阵的运算和实例
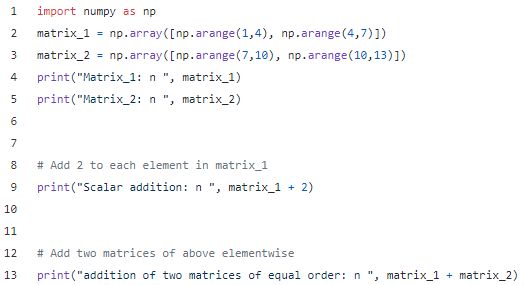
加法
下面的例子说明了两种加法形式:
标量的加法
矩阵的加法
输出:
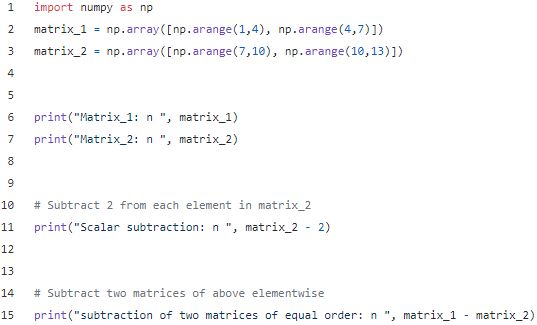
减法
减法相当于矩阵的加法,你只需要把加法改为减法即可。
输出:
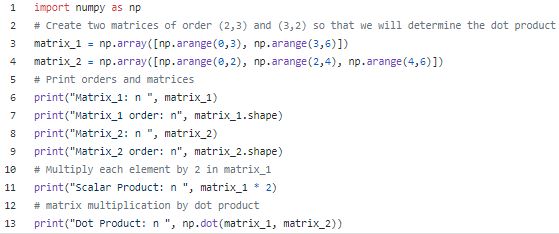
乘积
在 NumPy 矩阵中,可以执行两种乘法或乘积函数。
标量积:标量值与所有矩阵元素相乘
点乘积:这是根据矩阵的乘法规则得到的两个矩阵的乘积
重要提示: 注意 * 操作符仅用于标量乘法。我们使用一个函数 np.dot ()作为矩阵乘法的参数,该函数接受两个 numpy 2D 数组作为参数。
输出:
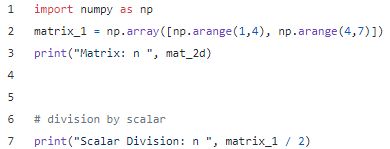
除法
元素级标量除法可以使用除法运算符/执行。
输出:
指数
可以使用运算符 * * 执行逐个元素的指数运算。
输出:
转置
矩阵的换位是一个包含初始列行的新矩阵。
一个矩阵序(2,3)在新的矩阵中变成(3,2)。
Numpy 具有在任何 ndarray 实体中转换矩阵的特性。我们不需要一个特定的运算符就可以找到一个矩阵转换。
下面的程序显示转置操作Matrix. T。
输出:
4. 如何执行矩阵切片
矩阵切片是子矩阵的发现,Python 为索引和切片矩阵提供了更好的语法。
切片使用了上面提到的语法:
矩阵[行索引范围,列索引范围,步骤号]
行和列索引范围遵循典型的起始索引 Python 语法: end index
当代码运行时,所选范围都是从开始索引到(结束索引 -1)
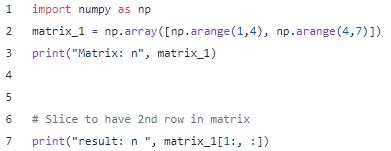
切片选择行
输出:
注意:行范围选择1意味着从索引1到最后一行选择行。列范围索引表示选择所选行范围中的所有列。
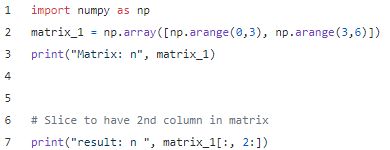
切片选择列
输出:
注意: 行范围选择意味着选择所有行。列范围索引2意味着选择从索引2开始到最后一列的所有列。
分片选择子矩阵
输出:
注意: 行范围选择1:3选择索引为1到2的行。列范围选择1:3将选择索引为1至2的列。
求解线性方程组
方程组
矩阵计算线性方程组的语法是:
R = np.dot((Inverse of P), Q)
其中:
r = 未知数的向量
p = 左边的元素系数
q = 右边的值
例如,考虑下面的线性方程组:
x + y + z = 1
2x + 4y + z =-2
x-y + z = 0
它是以矩阵形式构成的:
R = [ x y z ]未知数的向量
P = [ [1. 1 1] [2 4 1] [1 -1 1] ]
Q = [1 -2 0]
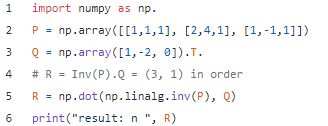
使用前面解释的矩阵语法,您将对方程组求解如下:
输出:
result:
[-4.5 0.5 5.]
其中 x =-4.5,y = 0.5,z = 5.0。
我相信你已经学会了如何在 Python 中实现矩阵。如果你有任何建议,请后台联系我吖。
· END ·
HAPPY LIFE
![]()