论文翻译:Dual-path RNN: efficient long sequence modeling for time-domain single-channel speech separatio
论文出处:
https://arxiv.org/abs/1910.06379
摘要
近年来基于深度学习的语音分离研究证明了时域方法相对于传统的时频分离方法的优越性。与时频域方法不同的是,时域分离系统经常接收到包含大量时间步长的输入序列,这给极长的序列建模带来了挑战。传统的递归神经网络(rnn)由于优化困难,不能有效地对这类长序列进行建模,而一维卷积神经网络(1-D cnn)在接受域小于序列长度时无法进行话语级序列建模。在本文中,我们提出了一种简单而有效的方法,将**双路径循环神经网络(DPRNN)**组织在深层结构中,以模拟极长的序列。DPRNN将长序列输入分割成更小的块,并迭代地应用块内和块间操作,其中在每次操作中,输入长度可以与原始序列长度的平方根成正比。实验表明,通过将一维CNN替换为DPRNN,并在时域音频分离网络(TasNet)中应用采样级建模,WSJ02mix在比之前的最佳系统小20倍的模型下实现了新的最先进的性能。
1. 简介
基于深度学习的语音分离技术的最新进展,引起了研究界对时域方法的兴趣。与标准的时频域方法相比,时域方法旨在联合建模幅度和相位信息,并允许对时频域可微准则进行直接优化。
目前的时域分离系统主要分为自适应前端方法和直接回归方法。自适应前端方法的目的是用可微变换取代短时傅里叶变换(STFT),构建一个可与分离网络共同学习的前端。与将分离过程应用于频谱图输入的传统时频域方法一样,分离应用于前端输出。这些系统独立于传统的时频分析范式,能够在窗口大小和前端基本功能的数量上有更灵活的选择。另一方面,直接回归方法从输入混合物中学习回归函数∗在微软研究院实习期间完成的作品。通常是通过使用某种形式的一维卷积神经网络(1-D cnn)来获取没有明确前端的底层干净信号。
这两个类别之间的一个共同点是,它们都依赖于对极长输入序列的有效建模。直接回归方法在波形样本水平上进行分离,而样本的数量通常可达数万,有时甚至更多。自适应前端方法的性能也取决于窗口大小的选择,其中较小的窗口以显著延长前端表示为代价提高了分离性能。这给传统的序列建模网络(包括rnn和一维cnn)带来了额外的挑战,因为它们难以学习这种长期的时间依赖性。此外,与具有动态接受域的RNNs不同,具有固定接受域且小于序列长度的一维cnn无法充分利用序列级依赖关系。
在本文中,我们提出了一个简单的网络结构,我们称之为双路径RNN (DPRNN),它组织任何类型的RNN层,以一种非常简单的方式建模长顺序输入。其原理是将输入序列分割成更短的块,并交替使用两个RNN,一个块内RNN和一个块间RNN,分别用于局部建模和全局建模。在一个DPRNN块中,块内RNN首先对局部块进行独立处理,然后块间RNN对所有块的信息进行聚合,进行话语级处理。对于长度为L的序列输入,chunk size K和chunk hop size P的DPRNN包含S个chunk,其中K和S分别对应于chunk间和chunk内rnn的输入长度。当K≈S时,两个rnn的输入长度为次线性(O(√L)),而不是原始的输入长度(O(L)),这大大降低了当L非常大时的优化难度。
相比于其他安排局部和全局RNN层的方法,或更通用于在多个时间尺度上进行序列建模的分层RNN,堆叠的DPRNN块迭代地交替执行块内和块间操作,可以将其视为局部输入和全局输入之间的交错处理。此外,在大多数分层RNN中,第一RNN层仍然接收整个输入序列,而在堆叠的DPRNN中,每个块内或块间的RNN在所有块中接收相同的次线性输入大小。与基于cnn的体系结构,如时间卷积网络(TCNs),由于接收域固定,只能进行局部建模相比,DPRNN能够通过块间RNNs充分利用全局信息,以更小的模型尺寸获得更优的性能。在第4节中,我们将表明,在先前提出的时域分离系统[4]中,只需简单地用DPRNN替换TCN,模型就能够在WSJ0-2mix上实现0.7 dB(4.6%)相对于比例不变信噪比(SI-SNR)的相对改进,模型尺寸减小49%。通过在波形样本水平进行分离,即2个样本的窗口大小和1个样本的跳跃大小,一个新的最先进的性能是实现了一个比以前最好的系统小20倍的模型。
2. 双路递归神经网络
2.1 模型设计
双路径RNN (DPRNN)包括三个阶段:分割、块处理和重叠添加。分割阶段将一个连续的输入分割成重叠的块,并将所有的块连接成一个三维张量。张量然后传递到堆叠的DPRNN块,以交替的方式迭代应用局部(块内)和全局(块间)建模。最后一层的输出用重叠叠加的方法转换回序列输出。图1显示了该模型的流程图。
2.1.1. 分离
对于顺序输入 W ∈ R N × L {\bf{W}} \in {\mathbb{R}^{N \times L}} % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaaqaaaaaaaaaWdbiaahEfacqGHiiIZtuuD % JXwAK1uy0HMmaeXbfv3ySLgzG0uy0HgiuD3BaGGbaiab-1ris9aada % ahaaWcbeqaa8qacaWGobGaey41aqRaamitaaaaaaa!5063! W∈RN×L其中N为特征维,L为时间步长,分割阶段将W分割为长度为K,跳数为P的块。第一个和最后一个块是零填充物,因此W中的每个样本都出现并且只出现在K/P块中,生成S等大小块 D s ∈ R N × K {{\bf{D}}_s} \in {\mathbb{R}^{N \times K}} % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaaqaaaaaaaaaWdbiaahseapaWaaSbaaSqa % a8qacaWGZbaapaqabaGcpeGaeyicI48efv3ySLgznfgDOjdarCqr1n % gBPrginfgDObcv39gaiyaacqWFDeIupaWaaWbaaSqabeaapeGaamOt % aiabgEna0kaadUeaaaaaaa!51BB! Ds∈RN×KS = 1,…然后,所有的块串联在一起,形成一个三维张量 T = [ D 1 , … , D S ] ∈ R N × K × S {\bf{T}} = \left[ {{{\bf{D}}_1}, \ldots ,{{\bf{D}}_S}} \right] \in {\mathbb{R}^{N \times K \times S}} % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaaqaaaaaaaaaWdbiaahsfacqGH9aqpdaWa % daWdaeaapeGaaCira8aadaWgaaWcbaWdbiaaigdaa8aabeaak8qaca % GGSaGaeyOjGWRaaiilaiaahseapaWaaSbaaSqaa8qacaWGtbaapaqa % baaak8qacaGLBbGaayzxaaGaeyicI48efv3ySLgznfgDOjdarCqr1n % gBPrginfgDObcv39gaiyaacqWFDeIupaWaaWbaaSqabeaapeGaamOt % aiabgEna0kaadUeacqGHxdaTcaWGtbaaaOGaaiOlaaaa!5E24! T=[D1,…,DS]∈RN×K×S
2.1.2 块处理
然后将分割输出T传递给B DPRNN块的堆栈。每个块将一个输入的三维张量转换成另一个形状相同的张量。我们表示块b = 1的输入张量,…,B为 T b ∈ R N × K × S {{\bf{T}}_b} \in {\mathbb{R}^{N \times K \times S}} % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaaqaaaaaaaaaWdbiaahsfapaWaaSbaaSqa % a8qacaWGIbaapaqabaGcpeGaeyicI48efv3ySLgznfgDOjdarCqr1n % gBPrginfgDObcv39gaiyaacqWFDeIupaWaaWbaaSqabeaapeGaamOt % aiabgEna0kaadUeacqGHxdaTcaWGtbaaaaaa!54A9! Tb∈RN×K×S其中T1 = T。每个块包含两个子模块,分别对应于块内处理和块间处理。块内RNN始终是双向的,应用于Tb的第2维,即每个S块内: U b = [ f b ( T b [ : , : , i ] ) , i = 1 , … , S ] {{\bf{U}}_b} = \left[ {{f_b}\left( {{{\bf{T}}_b}[:,:,i]} \right),i = 1, \ldots ,S} \right] % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaaqaaaaaaaaaWdbiaahwfapaWaaSbaaSqa % a8qacaWGIbaapaqabaGcpeGaeyypa0ZaamWaa8aabaWdbiaadAgapa % WaaSbaaSqaa8qacaWGIbaapaqabaGcpeWaaeWaa8aabaWdbiaahsfa % paWaaSbaaSqaa8qacaWGIbaapaqabaGcpeGaai4waiaacQdacaGGSa % GaaiOoaiaacYcacaWGPbGaaiyxaaGaayjkaiaawMcaaiaacYcacaWG % PbGaeyypa0JaaGymaiaacYcacqGHMacVcaGGSaGaam4uaaGaay5wai % aaw2faaaaa!5763! Ub=[fb(Tb[:,:,i]),i=1,…,S]
其中 U b ∈ R H × K × S {{\bf{U}}_b} \in {\mathbb{R}^{H \times K \times S}} % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaaqaaaaaaaaaWdbiaahwfapaWaaSbaaSqa % a8qacaWGIbaapaqabaGcpeGaeyicI48efv3ySLgznfgDOjdarCqr1n % gBPrginfgDObcv39gaiyaacqWFDeIupaWaaWbaaSqabeaapeGaamis % aiabgEna0kaadUeacqGHxdaTcaWGtbaaaaaa!54A4! Ub∈RH×K×S为RNN的输出,fb(·)是RNN定义的映射函数,并且 T b [ : , : , i ] ∈ R N × K {{\bf{T}}_b}[:,:,i] \in {\mathbb{R}^{N \times K}} % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaaqaaaaaaaaaWdbiaahsfapaWaaSbaaSqa % a8qacaWGIbaapaqabaGcpeGaai4waiaacQdacaGGSaGaaiOoaiaacY % cacaWGPbGaaiyxaiabgIGioprr1ngBPrwtHrhAYaqehuuDJXwAKbst % HrhAGq1DVbacgaGae8xhHi1damaaCaaaleqabaWdbiaad6eacqGHxd % aTcaWGlbaaaaaa!5744! Tb[:,:,i]∈RN×K是块i定义的序列,然后应用线性全连接层(FC)将Ub的特征维度转换回Tb的特征维度: U ^ b = [ G U b [ : , : , i ] + m , i = 1 , … , S ] {{\bf{\hat U}}_b} = \left[ {{\bf{G}}{{\bf{U}}_b}[:,:,i] + {\bf{m}},i = 1, \ldots ,S} \right] % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaaqaaaaaaaaaWdbiqahwfapaGbaKaadaWg % aaWcbaWdbiaadkgaa8aabeaak8qacqGH9aqpdaWadaWdaeaapeGaaC % 4raiaahwfapaWaaSbaaSqaa8qacaWGIbaapaqabaGcpeGaai4waiaa % cQdacaGGSaGaaiOoaiaacYcacaWGPbGaaiyxaiabgUcaRiaah2gaca % GGSaGaamyAaiabg2da9iaaigdacaGGSaGaeyOjGWRaaiilaiaadofa % aiaawUfacaGLDbaaaaa!562E! U^b=[GUb[:,:,i]+m,i=1,…,S]
其中 U ^ ∈ R N × K × S {\bf{\hat U}} \in {\mathbb{R}^{N \times K \times S}} % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaaqaaaaaaaaaWdbiqahwfapaGbaKaapeGa % eyicI48efv3ySLgznfgDOjdarCqr1ngBPrginfgDObcv39gaiyaacq % WFDeIupaWaaWbaaSqabeaapeGaamOtaiabgEna0kaadUeacqGHxdaT % caWGtbaaaaaa!537E! U^∈RN×K×S是变换后的特征。
G ∈ R N × H {\bf{G}} \in {\mathbb{R}^{N \times H}} % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaaqaaaaaaaaaWdbiaahEeacqGHiiIZtuuD % JXwAK1uy0HMmaeXbfv3ySLgzG0uy0HgiuD3BaGGbaiab-1ris9aada % ahaaWcbeqaa8qacaWGobGaey41aqRaamisaaaaaaa!504F! G∈RN×H和
m ∈ R N × 1 {\bf{m}} \in {\mathbb{R}^{N \times 1}} % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaaqaaaaaaaaaWdbiaah2gacqGHiiIZtuuD % JXwAK1uy0HMmaeXbfv3ySLgzG0uy0HgiuD3BaGGbaiab-1ris9aada % ahaaWcbeqaa8qacaWGobGaey41aqRaaGymaaaaaaa!5063! m∈RN×1分别是全连接层的权重和偏置。
U b [ : , : , i ] ∈ R H × K {{\bf{U}}_b}[:,:,i] \in {\mathbb{R}^{H \times K}} % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaaqaaaaaaaaaWdbiaahwfapaWaaSbaaSqa % a8qacaWGIbaapaqabaGcpeGaai4waiaacQdacaGGSaGaaiOoaiaacY % cacaWGPbGaaiyxaiabgIGioprr1ngBPrwtHrhAYaqehuuDJXwAKbst % HrhAGq1DVbacgaGae8xhHi1damaaCaaaleqabaWdbiaadIeacqGHxd % aTcaWGlbaaaaaa!573F! Ub[:,:,i]∈RH×K代表Ub中的第i块,然后将层归一化(LN)应用于ˆU,我们根据经验发现,这对于模型具有良好的泛化能力非常重要:

其中z,r∈ RN×1是重缩放因子,µ(·)和σ(·)是定义为的三维张量的均值和方差:

然后在LN操作的输出和输入Tb之间加上一个剩余的连接: T ^ b = T b + L N ( U ^ b ) {{\bf{\hat T}}_b} = {{\bf{T}}_b} + LN\left( {{{{\bf{\hat U}}}_b}} \right) % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaaqaaaaaaaaaWdbiqahsfapaGbaKaadaWg % aaWcbaWdbiaadkgaa8aabeaak8qacqGH9aqpcaWHubWdamaaBaaale % aapeGaamOyaaWdaeqaaOWdbiabgUcaRiaadYeacaWGobWaaeWaa8aa % baWdbiqahwfapaGbaKaadaWgaaWcbaWdbiaadkgaa8aabeaaaOWdbi % aawIcacaGLPaaaaaa!4B3B! T^b=Tb+LN(U^b)然后将Tb作为块间RNN子模块的输入,其中将RNN应用于最后一个维,即每个S块中对齐的K个时间步长: V b = [ h b ( T ^ b [ : , i , : ] ) , i = 1 , … , K ] {{\bf{V}}_b} = \left[ {{h_b}\left( {{{{\bf{\hat T}}}_b}[:,i,:]} \right),i = 1, \ldots ,K} \right] % MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai % aabeqaamaabaabauaakeaaqaaaaaaaaaWdbiaahAfapaWaaSbaaSqa % a8qacaWGIbaapaqabaGcpeGaeyypa0ZaamWaa8aabaWdbiaadIgapa % WaaSbaaSqaa8qacaWGIbaapaqabaGcpeWaaeWaa8aabaWdbiqahsfa % paGbaKaadaWgaaWcbaWdbiaadkgaa8aabeaak8qacaGGBbGaaiOoai % aacYcacaWGPbGaaiilaiaacQdacaGGDbaacaGLOaGaayzkaaGaaiil % aiaadMgacqGH9aqpcaaIXaGaaiilaiabgAci8kaacYcacaWGlbaaca % GLBbGaayzxaaaaaa!576E! Vb=[hb(T^b[:,i,:]),i=1,…,K]其中Vb是RNN的输出,其中Vb∈R^(H×K×S)是RNN的输出,hb(·)是RNN定义的映射函数,ˆTb[:, i,:]∈R^(N ×S)是所有S块中第i个时间步长定义的序列。由于块内RNN是双向的,ˆTb中的每一个时间步都包含了它所属块的全部信息,这使得块间RNN可以进行全序列级建模。与intrachunk RNN一样,线性FC层和LN操作是在Vb之上应用的。在output和ˆTb之间还增加了一个剩余的连接,构成了DPRNN block b的输出。当b < b时,输出作为下一个block T(b+1)的输入。
2.1.3 重叠相加
在上一节中最后一个DPRNN块的输出为T(b+1)∈R^(N ×K×S)。为了将其转换回序列,对S块应用重叠加的方法,形成输出Q∈R(N ×L)。
2.2. 讨论
考虑单个块内和块间RNNs的输入序列长度之和,用K + S表示,其中跳数大小设置为50%(即P = K/2),如图1所示。很容易看出,S = d(2L/K)e + 1,其中d(·)e是上限函数。为了使总输入长度K + S = K + d(2L/K)e + 1最小,K取K≈√2L,那么S也满足S≈√2L≈K,这样得到的是次线性输入长度O(√L),而不是原来的线性输入长度O(L)。
对于需要在线处理的任务,块间RNN可以进行单向扫描,从第一个块扫描到当前块。后仍然可以利用信息块从以前所有块,因此延迟最小系统定义的块大小k .这是与标准CNN-based模型只能进行本地处理由于thefixed receptivefield或传统RNN-based模型执行框架水准仪代替chunk-level建模。但是,在线和离线设置之间的性能差异超出了本文的范围。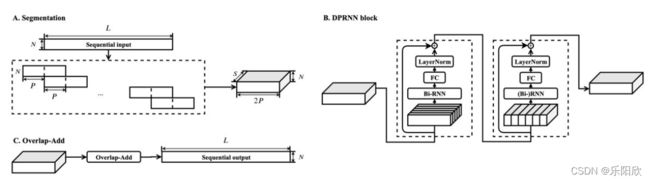
图为双路径RNN (DPRNN)系统流程图。(A)分割阶段将一个连续的输入分割成有或没有重叠的块,并将它们连接起来形成一个三维张量。在我们的实现中,重叠比例被设置为50%。(B)每个DPRNN块由两个具有不同维度循环连接的rnn组成。首先将块内双向RNN并行应用于单个块,以处理局部信息。然后跨块应用块间RNN以捕获全局依赖关系。可对多个块进行叠加,增加网络的总深度。©将最后一个DPRNN块的三维输出通过对块进行叠加转换为顺序输出。
3 实验程序
3.1 模型配置
虽然DPRNN可以应用于任何需要长期序列建模的系统,但我们研究了它在时域音频分离网络(TasNet)中的应用,这是一种自适应前端方法,可以在基准数据集上实现高语音分离性能。TasNet包含三个部分:(1)线性一维卷积编码器,它封装了输入波形为一个混合自适应二维前端表示,(2)一个分离器估计掩蔽矩阵C目标来源,和(3)线性一维转置卷积译码器转换回波形蒙面的二维表示。我们使用与[4]中相同的编码器和解码器设计,而数字过滤器被设置为64。对于分离器,我们将提出的深度DPRNN与[4]中描述的优化配置的TCN进行了比较。我们使用6个DPRNN块,使用BLSTM作为块内和块间rnn,每个方向有128个隐藏单元。DPRNN的块大小K是根据前端表示的长度经验定义的,即在训练集中K≈√2L,如2.2节所述。
3.2 数据集
我们评估了我们的方法在两说话人语音分离和识别任务。仅分离实验是在广泛使用的WSJ0-2mix数据集上进行的。WSJ0-2mix包含从《华尔街日报》(WSJ0) si tr s集生成的30小时8k Hz训练数据。它也有10小时的验证数据和5小时的测试数据产生的si dt 05和si et 05组。每种混合都是通过从相应的组中随机选择不同的扬声器,并以-5到5 dB之间的随机相对信噪比(SNR)进行混合而人为产生的。在语音分离与识别实验中,我们分别从Librispeech数据集中采样200小时和10小时的人工混合噪声混响混合物进行训练和验证。将16khz信号与图像方法产生的房间脉冲响应进行卷积。房间的长宽在2 - 10米之间随机采样,高度在2 - 5米之间随机采样。混响时间(T60)在0.1和0.5秒之间随机采样。扬声器和单个麦克风的位置都是随机取样的。两个混响信号被重新调整为-5到5 dB之间的随机信噪比,并进一步移位,使两个扬声器之间的重叠率平均为50%。在10 ~ 20 dB的随机信噪比下,合成的混合物进一步受到随机各向同性噪声的破坏。为了进行评估,我们以同样的方式从微软内部的由44个发言者组成的性别平衡的干净演讲集合中采样,生成混合语音。分离的目标是为两个发言者的混响干净的讲话。
3.3 实验配置
我们在4秒长的片段上训练100个时代的所有模型。学习速率初始化为1e−3,每两个epoch衰减0.98。如果连续10个时期在验证集中没有发现最佳模型,则采用提前停止。Adam被用作优化器。所有实验均采用最大l2范数为5的梯度裁剪。所有模型都使用话语级置换不变训练(uPIT)进行训练,以最大化尺度不变信噪比(SI-SNR)。从信号保真度和语音识别精度两个方面评估了系统的有效性。信号保真度的改善程度是通过信噪比改善(SDRi)和SI-SNR改善(SISNRi)来衡量的。语音识别的准确性是由两个分开的说话人的单词错误率(WER)来衡量的。
4. 结果与讨论
4.1 在WSJ0-2mix数据集上的结果
我们首先报告WSJ0-2mix数据集上的结果。表1比较了基于tasnet的不同隔离网络的系统。可以看出,单纯用DPRNN替代TCN,分离性能提高了4.6%,模型缩小了49%。这显示了本文提出的局部全局建模比以前基于cnn的局部唯一建模的优越性。此外,通过进一步减小编码器和解码器中的滤波器长度(以及因此而产生的跳数大小),可以持续地提高性能。当滤波器长度为2个采样,编码器输出帧数超过30000帧时,获得了最佳性能。这对于标准的RNNs或cnn来说是非常困难的,甚至是不可能的,而对于拟议的DPRNN,使用这样的短滤波器成为可能,并获得最佳性能。表2将DPRNN-TasNet与WSJ0-2mix上的其他系统进行了比较。我们可以看到,DPRNN-TasNet实现了SI-SNRi的新记录,其模型比FurcaNeXt(先前的最先进的系统)小20倍。DPRNN-TasNet模型体积小,性能优越,表明无需使用庞大或复杂的模型即可解决WSJ0-2mix数据集上的语音分离问题,表明在未来的研究中需要使用更具挑战性和更真实的数据集。
表1:基于tasnet的语音分离系统中WSJ0-2mix的不同分离网络和配置的比较。之前的工作使用了TCN-TasNet。
表2:WSJ0-2mix与其他方法的比较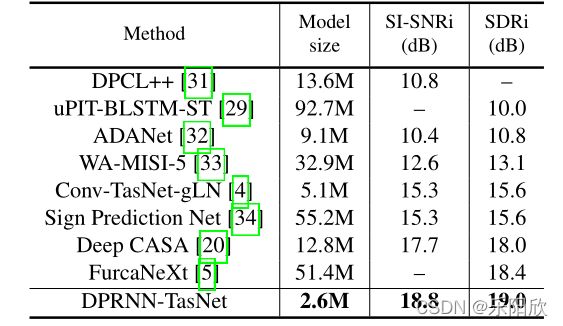
表3:SI-SNRi和WER结果用于噪声混响的分离和识别任务。两个模型的窗口大小设置为32个样本,DPRNN-TasNet的块大小设置为100帧。对两个分离的说话人计算WER

4.2 语音分割与识别的结果
我们使用传统的混合系统进行语音识别。我们的识别系统是在从各种来源[35]收集到的大规模单扬声器噪声混响语音上训练的。表3比较了基于TCN和基于dprnn的TasNet模型的2 ms窗口(32个样本,16 kHz采样率)。我们可以观察到,DPRNN- tasnet在SISNRi和WER中的表现明显优于TCN-TasNet,这表明即使在具有挑战性的嘈杂和混响条件下,DPRNN也具有优势。这进一步表明,DPRNN可以在一系列任务和场景中替代传统的顺序建模模块。
5. 总结
在本文中,我们提出了双路径循环神经网络(DPRNN),这是一种简单而有效的方法来组织任何类型的RNN层来建模一个极长的序列。DPRNN将顺序输入分割为重叠的块,并执行块内(本地)和块间(全局)处理,有两个rnn交替迭代。该设计允许每个RNN输入的长度与原始输入长度的平方根成正比,实现了次线性处理,缓解了优化挑战。我们还描述了利用时域音频分离网络(TasNet)在单通道时域语音分离中的应用。通过将一维CNN模块替换为深度DPRNN,并在TasNet框架中进行样本级分离,WSJ0-2mix在比先前报道的最佳系统小20倍的模型下获得了新的最先进的性能。实验结果证明了DPRNN在具有挑战性的声学条件下的有效性。这些结果证明了所提出的方法在各种场景和任务中的优越性。