wzg2016
wzg2016

共轭复数，共轭根式，共轭矩阵，共轭方向，共轭方向法，共轭梯度法，共轭分布，共轭函数，傅里叶变换的共轭对称

目录

1. 共轭复数

2. 傅里叶变换的共轭对称性

3. 共轭根式(radical conjugates)

4. 共轭矩阵（自共轭矩阵、Hermitian（埃尔米特）矩阵）

5. 共轭方向

6. 共轭方向法

7. 共轭梯度法

8. 共轭分布(conjugacy)

9. 共轭函数（对偶函数、极化函数）

共轭（conjugate ）的概念在数学、物理、化学、地理等学科中都有出现。 本意：两头牛背上的架子称为轭，轭使两头牛同步行走。扩展到数学等领域，共轭即为按一定的规律相配的一对或一组。

共轭复数，共轭根式，共轭矩阵，共轭方向，共轭方向法，共轭梯度法，共轭分布，共轭函数，傅里叶变换的共轭对称_第1张图片

在数学中常见的共轭有：共轭复数，共轭根式，共轭矩阵，共轭转置，共轭分布，共轭先验，共轭函数, 共轭方向，共轭方向法，共轭梯度

法。

我们在关注共轭时，主要关注共轭的配对规律，共轭的性质，以及取共轭可以带来什么样的数学或应用优势。

1. 共轭复数

配对规律：在复数中，实部相等，虚部互为相反数的两个复数互为共轭复数。

公式描述：z=a+ib 与 \widetilde{z}=a-ib 互为复数

共轭性质：1）加和为实数

                  2）在复平面上，共轭复数所对应的点关于实轴对称

2. 傅里叶变换的共轭对称性

说明：这里的共轭就是上面介绍的复数共轭，不是指傅里叶变换与傅里叶反变换是一对共轭。

定义：

3. 共轭根式(radical conjugates)

配对规律：两个不等于零的根式A、B，若它们的积AB不含根式，则称A、B互为共轭根式。

共轭性质：通过相乘能把根式去掉。

描述：对根式的模式没有要求，只要满足配对规律的就都是共轭根式。

4. 共轭矩阵（自共轭矩阵、Hermitian（埃尔米特）矩阵）

描述：一般共轭矩阵是一个复数矩阵，实对称阵是Hermite阵的特例。

配对规律：矩阵中第i行第j列的元素与第j行第i列的元素互为共轭复数，的矩阵称为共轭矩阵。

公式描述：对于一个复数矩阵 A=(a_{ij}),如果a_{ij}=\widetilde{a_{ji}},则称A为共轭矩阵。

                  若用H表示矩阵的旋转取共轭操作（称为共轭转置操作），则满足A^{H}=A的矩阵是共轭矩阵。

性质：1）主对角线上的元素全是实数。

           2）若A 和B 是Hermite阵，那么它们的和A+B 也是Hermite阵

           3）若A 和B 是Hermite阵，如果满足AB=BA，那么AB与BA也是Hermite阵

           4）更多性质可参考《矩阵分析与应用（张贤达 第2版）》第101页。拥有很多很好的性质。

5. 共轭方向

组配对规律：对于一组n维的非零(列)向量\{v_1,v_2,v_3,...v_i,...v_j,...\}和一个n*n的对称正定矩阵 Q，若 v_{i}^{T}Qv_j=0，则称这组向量关于矩阵Q是互相共轭的。因为每个向量都可以表示一个方向，所以称为共轭方向。

描述：由定义可知，在高维空间中，一个方向向量的共轭方向不是唯一的，而是一组。

特例：当Q为单位矩阵时，v_{i}^{T}v_j=0，此时这组向量是正交的。由此可见，正交是共轭的一种特殊情况，共轭是正交的推广。

性质：1）互为共轭的一组向量，线性无关

           2）n维空间中，关于任何一个n*n的对称正定矩阵 Q， 非零的共轭向量个数不超过n。

6. 共轭方向法

描述：共轭方向法(conjugate direction method)一种沿着共轭方向寻找无约束最优化问题极小点的一类方法。

对于一个二次型函数f(\vec{x})=\frac{1}{2}\vec{x}^TG\vec{x} + \vec{b} ^T\vec{x} + c, 其中\vec{x}\in R^n,Q是一个正定对称矩阵，

给定关于 Q 的一组包含k(k<=n)个共轭向量的共轭向量组 \{ \vec{d^1},\vec{d^2},...,\vec{d^i},...,\vec{d^k} \} ,与一个初始搜索点\vec{x}^{(1)}，可以通过k次迭代，在\vec{x}^{(1)}与\{ \vec{d^1},\vec{d^2},...,\vec{d^i},...,\vec{d^k} \}张成的k维子空间中找到f(\vec{x})的极小值。每一次迭代都沿着一个新的共轭方向更新，沿该共轭方向的更新步长是一个解析解。

以下是来自共轭方向法 的摘抄。

共轭复数，共轭根式，共轭矩阵，共轭方向，共轭方向法，共轭梯度法，共轭分布，共轭函数，傅里叶变换的共轭对称_第2张图片

其中\alpha_k是沿 \vec{d}^{(k)} 方向的更新步长。\vec{d}^{(k)}是提前已知的。具体的公式证明可参考：《最优化方法（赖炎连 贺国平 主编）》的第三章，3.3节。

7. 共轭梯度法

描述：共轭梯度法可以看作一类特殊的共轭方向法，不同的是，共轭方向法在使用时需要预先定义好一组共轭方向向量。共轭梯度法克服这一缺点，共轭方向向量是随着迭代过程，当场生成下一次迭代的共轭方向。以下摘抄自：共轭梯度法

共轭复数，共轭根式，共轭矩阵，共轭方向，共轭方向法，共轭梯度法，共轭分布，共轭函数，傅里叶变换的共轭对称_第3张图片

其中\beta_{k}也是解析解，具体推论与证明可参考 《最优化方法（赖炎连 贺国平 主编）》的第三章，3.3节。。

8. 共轭分布(conjugacy)

配对规律：如果两个分布满足同样的分布律（形式相同，参数不同），那么这两个分布互称为共轭分布。

性质：分布的表达式相同，参数不同

描述：共轭分布概念通常出现在贝叶斯概率理论中，如果后验概率P(θ|X)和先验概率P(θ)满足同样的分布律(形式相同，参数不同)。那么，先验分布和后验分布被叫做共轭分布，同时，先验分布叫做似然函数的共轭先验（分布）。

9. 共轭函数（对偶函数、极化函数）

定义：设函数 f:R^n\rightarrow R, 定义函数f^*:R^n\rightarrow R为：

                                                       f^*(y)=\sup_{x\in dom f} (y^Tx-f(x)),

则函数f^*是函数f的共轭函数。其中dom f表示函数f的定义域。sup表示函数的上确界，即最小上界。y是共轭函数f^*的变量。

使f^*上确界有限（即 y^Tx-f(x) 在dom f 上有上确界）的所有的y\in R^n构成共轭函数f^*的定义域。下图描述了此定义。

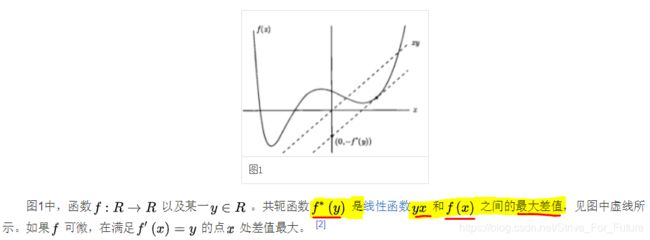
共轭复数，共轭根式，共轭矩阵，共轭方向，共轭方向法，共轭梯度法，共轭分布，共轭函数，傅里叶变换的共轭对称_第4张图片

特点：无论原函数f是否是凸函数，它的共轭函数f^*都是凸函数。

性质：1）凸函数的共轭函数的共轭函数是原函数，f^{**}=f。

           2）更多具体性质可参考《凸优化（王书宁 译）》第85页

相关：可微函数的共轭函数称为函数的Legendre变换。为了区分一般情况和可微情况下所定义的共轭，一般函数的共轭有时称为Fenchel共轭。

 

参考：[1] 连续时间傅里叶变换的共轭与共轭对称性（详细推导）

           [2]【机器学习之数学】02 梯度下降法、最速下降法、牛顿法、共轭方向法、拟牛顿法

           [3]《凸优化（王书宁 译）》

           [4]《最优化方法（赖炎连 贺国平 主编）》的第三章

你可能感兴趣的:(共轭复数，共轭根式，共轭矩阵，共轭方向，共轭方向法，共轭梯度法，共轭分布，共轭函数，傅里叶变换的共轭对称)

  • 斤斤计较的婚姻到底有多难？ 白心之岂必有为
    很多人私聊我会问到在哪个人群当中斤斤计较的人最多？我都会回答他，一般婚姻出现问题的斤斤计较的人士会非常多，以我多年经验，在婚姻落的一塌糊涂的人当中，斤斤计较的人数占比在20～30%以上，也就是说10个婚姻出现问题的斤斤计较的人有2-3个有多不减。在婚姻出问题当中，有大量的心理不平衡的、尖酸刻薄的怨妇。在婚姻中仅斤斤计较有两种类型：第一种是物质上的，另一种是精神上的。在物质与精神上抠门已经严重的影响
  • 情绪觉察日记第37天 露露_e800
    今天是家庭关系规划师的第二阶最后一天，慧萍老师帮我做了个案，帮我处理了埋在心底好多年的一份恐惧，并给了我深深的力量！这几天出来学习，爸妈过来婆家帮我带小孩，妈妈出于爱帮我收拾东西，并跟我先生和婆婆产生矛盾，妈妈觉得他们没有照顾好我…。今晚回家见到妈妈，我很欣赏她并赞扬她，妈妈说今晚要跟我睡我说好，当我们俩躺在床上准备睡觉的时候，我握着妈妈的手对她说:妈妈这几天辛苦你了，你看你多利害把我们的家收拾得
  • 芦花鞋一四 许叶晗
    又是在一个寒冷的夏日里，青铜和葵花决定今天一起去卖芦花鞋，奶奶亲手给他们做了一碗热乎乎的粥对他们说:“就靠你们两挣生活费了这碗粥赶紧趁热喝了吧！”于是青铜和葵花喝完了奶奶给她们做的粥，就准备去镇上卖卢花鞋，这回青铜和葵花穿着新的芦花鞋来到了镇上。青铜这回看到了很多人都在卖，用手势表达对葵花说:“这回有好多人在抢我们生意呢！我们必须得吆喝起来。”葵花点了点头。可是谁知他们也大声的叫，卖芦花喽！卖芦花
  • QQ群采集助手，精准引流必备神器 2401_87347160 其他经验分享
    功能概述微信群查找与筛选工具是一款专为微信用户设计的辅助工具，它通过关键词搜索功能，帮助用户快速找到相关的微信群，并提供筛选是否需要验证的群组的功能。主要功能关键词搜索：用户可以输入关键词，工具将自动查找包含该关键词的微信群。筛选功能：工具提供筛选机制，用户可以选择是否只显示需要验证或不需要验证的群组。精准引流：通过上述功能，用户可以更精准地找到目标群组，进行有效的引流操作。3.设备需求该工具可以
  • 关于沟通这件事，项目经理不需要每次都面对面进行 流程大师兄
    很多项目经理都会遇到这样的问题，项目中由于事情太多，根本没有足够的时间去召开会议，那在这种情况下如何去有效地管理项目中的利益相关者？当然，不建议电子邮件也不需要开会的话，建议可以采取下面几种方式来形成有效的沟通，这几种方式可以帮助你努力的通过各种办法来保持和各方面的联系。项目经理首先要问自己几个问题，项目中哪些利益相关者是必须要进行沟通的？可以列出项目中所有的利益相关者清单，同时也整理出项目中哪些
  • 机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习python
    一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
  • 铭刻于星（四十二） 随风至
    69夜晚，绍敏同学做完功课后，看了眼房外，没听到动静才敢从书包的夹层里拿出那个心形纸团。折痕压得很深，都有些旧了，想来是已经写好很久了。绍敏同学慢慢地、轻轻地捏开折叠处，待到全部拆开后，又反复抚平纸张，然后仔细地一字字默看。只是开头的三个字是第一次看到，让她心漏跳了几拍。“亲爱的绍敏：从四年级的时候，我就喜欢你了，但是我一直不敢说，怕影响你学习。六年级的时候听说有人跟你表白，你接受了，我很难过，但
  • 底层逆袭到底有多难，不甘平凡的你准备好了吗？让吴起给你说说 造命者说
    底层逆袭到底有多难，不甘平凡的你准备好了吗？让吴起给你说说我叫吴起，生于公元前440年的战国初期，正是群雄并起、天下纷争不断的时候。后人说我是军事家、政治家、改革家，是兵家代表人物。评价我一生历仕鲁、魏、楚三国，通晓兵家、法家、儒家三家思想，在内政军事上都有极高的成就。周安王二十一年（公元前381年），因变法得罪守旧贵族，被人乱箭射死。我出生在卫国一个“家累万金”的富有家庭，从年轻时候起就不甘平凡
  • 2020-01-25 晴岚85
    郑海燕坚持分享590天2020.1.24在生活中只存在两个问题。一个问题是：你知道想要达成的目标是什么，但却不知道如何才能达成；另一个问题是：你不知道你的目标是什么。前一个是行动的问题，后一个是结果的问题。通过制定具体的下一步行动，可以解决不知道如何开始行动的问题。而通过去想象结果，对结果做预估，可以解决找不着目标的问题。对于所有吸引我们注意力，想要完成的任务，你可以先想象一下，预期的结果究竟是什
  • 随笔 | 仙一般的灵气 海思沧海
    仙岛今天，我看了你全部，似乎已经进入你的世界我不知道，这是否是梦幻，还是你仙一般的灵气吸引了我也许每一个人都要有一份属于自己的追求，这样才能够符合人生的梦想，生活才能够充满着阳光与快乐我不知道，我为什么会这样的感叹，是在感叹自己的人生，还是感叹自己一直没有孜孜不倦的追求只感觉虚度了光阴，每天活在自己的梦中，活在一个不真实的世界是在逃避自己，还是在逃避周围的一切有时候我嘲笑自己，嘲笑自己如此的虚无，
  • 想家 爆米花机
    也许不同于大家对家乡的思念，我对家乡甚至是疯狂的不舍。还未踏出车站就感觉到幸福，我享受这里的夕阳、这里的浓烈柴火味、这里每一口家常菜。我是宅女，我贪恋家的安逸。刚刚踏出大学校门，初出茅庐，无法适应每年只能国庆和春节回家。我焦虑、失眠、无端发脾气，是无法适应工作的节奏，是无法接受我将一步步离开家乡的事实。我不想承认自己胸无大志，选择再次踏上征程。图片发自App
  • 【iOS】MVC设计模式 Magnetic_h iosmvc设计模式objective-c学习ui
    MVC前言如何设计一个程序的结构，这是一门专门的学问，叫做"架构模式"（architecturalpattern），属于编程的方法论。MVC模式就是架构模式的一种。它是Apple官方推荐的App开发架构，也是一般开发者最先遇到、最经典的架构。MVC各层controller层Controller/ViewController/VC（控制器）负责协调Model和View，处理大部分逻辑它将数据从Mod
  • OC语言多界面传值五大方式 Magnetic_h iosui学习objective-c开发语言
    前言在完成暑假仿写项目时，遇到了许多需要用到多界面传值的地方，这篇博客来总结一下比较常用的五种多界面传值的方式。属性传值属性传值一般用前一个界面向后一个界面传值，简单地说就是通过访问后一个视图控制器的属性来为它赋值，通过这个属性来做到从前一个界面向后一个界面传值。首先在后一个界面中定义属性@interfaceBViewController:UIViewController@propertyNSSt
  • 一百九十四章. 自相矛盾 巨木擎天
    唉！就这么一夜，林子感觉就像过了很多天似的，先是回了阳间家里，遇到了那么多不可思议的事情儿。特别是小伙伴们，第二次与自己见面时，僵硬的表情和恐怖的气氛，让自己如坐针毡，打从心眼里难受！还有东子，他现在还好吗？有没有被人欺负？护城河里的小鱼小虾们，还都在吗？水不会真的干枯了吧？那对相亲相爱漂亮的太平鸟儿，还好吧！春天了，到了做窝、下蛋、喂养小鸟宝宝的时候了，希望它们都能够平安啊！虽然没有看见家人，也
  • UI学习——cell的复用和自定义cell Magnetic_h ui学习
    目录cell的复用手动（非注册）自动（注册）自定义cellcell的复用在iOS开发中，单元格复用是一种提高表格（UITableView）和集合视图（UICollectionView）滚动性能的技术。当一个UITableViewCell或UICollectionViewCell首次需要显示时，如果没有可复用的单元格，则视图会创建一个新的单元格。一旦这个单元格滚动出屏幕，它就不会被销毁。相反，它被添
  • element实现动态路由+面包屑 软件技术NINI vue案例vue.js前端
    el-breadcrumb是ElementUI组件库中的一个面包屑导航组件，它用于显示当前页面的路径，帮助用户快速理解和导航到应用的各个部分。在Vue.js项目中，如果你已经安装了ElementUI，就可以很方便地使用el-breadcrumb组件。以下是一个基本的使用示例：安装ElementUI（如果你还没有安装的话）:你可以通过npm或yarn来安装ElementUI。bash复制代码npmi
  • 10月|愿你的青春不负梦想-读书笔记-01 Tracy的小书斋
    本书的作者是俞敏洪，大家都很熟悉他了吧。俞敏洪老师是我行业的领头羊吧，也是我事业上的偶像。本日摘录他书中第一章中的金句：『一个人如果什么目标都没有，就会浑浑噩噩，感觉生命中缺少能量。能给我们能量的，是对未来的期待。第一件事，我始终为了进步而努力。与其追寻全世界的骏马，不如种植丰美的草原，到时骏马自然会来。第二件事，我始终有阶段性的目标。什么东西能给我能量？答案是对未来的期待。』读到这里的时候，我便
  • C语言宏函数 南林yan C语言c语言
    一、什么是宏函数？通过宏定义的函数是宏函数。如下，编译器在预处理阶段会将Add(x,y)替换为((x)*(y))#defineAdd(x,y)((x)*(y))#defineAdd(x,y)((x)*(y))intmain(){inta=10;intb=20;intd=10;intc=Add(a+d,b)*2;cout<
  • 地推话术，如何应对地推过程中家长的拒绝 校师学
    相信校长们在做地推的时候经常遇到这种情况：市场专员反馈家长不接单，咨询师反馈难以邀约这些家长上门，校区地推疲软，招生难。为什么？仅从地推层面分析，一方面因为家长受到的信息轰炸越来越多，对信息越来越“免疫”；而另一方面地推人员的专业能力和营销话术没有提高，无法应对家长的拒绝，对有意向的家长也不知如何跟进，眼睁睁看着家长走远；对于家长的疑问，更不知道如何有技巧地回答，机会白白流失。由于回答没技巧和专业
  • 谢谢你们，爱你们！ 鹿游儿
    昨天家人去泡温泉，二个孩子也带着去，出发前一晚，匆匆下班，赶回家和孩子一起收拾。饭后，我拿出笔和本子（上次去澳门时做手帐的本子）写下了1\2\3\4\5\6\7\8\9,让后让小壹去思考，带什么出发去旅游呢？她在对应的数字旁边画上了，泳衣、泳圈、肖恩、内衣内裤、tapuy、拖鞋……画完后，就让她自己对着这个本子，将要带的，一一带上，没想到这次带的书还是这本《便便工厂》(晚上姑婆发照片过来，妹妹累得
  • C语言如何定义宏函数？ 小九格物 c语言
    在C语言中，宏函数是通过预处理器定义的，它在编译之前替换代码中的宏调用。宏函数可以模拟函数的行为，但它们不是真正的函数，因为它们在编译时不会进行类型检查，也不会分配存储空间。宏函数的定义通常使用#define指令，后面跟着宏的名称和参数列表，以及宏展开后的代码。宏函数的定义方式：1.基本宏函数：这是最简单的宏函数形式，它直接定义一个表达式。#defineSQUARE(x)((x)*(x))2.带参
  • 微服务下功能权限与数据权限的设计与实现 nbsaas-boot 微服务java架构
    在微服务架构下，系统的功能权限和数据权限控制显得尤为重要。随着系统规模的扩大和微服务数量的增加，如何保证不同用户和服务之间的访问权限准确、细粒度地控制，成为设计安全策略的关键。本文将讨论如何在微服务体系中设计和实现功能权限与数据权限控制。1.功能权限与数据权限的定义功能权限：指用户或系统角色对特定功能的访问权限。通常是某个用户角色能否执行某个操作，比如查看订单、创建订单、修改用户资料等。数据权限：
  • 理解Gunicorn：Python WSGI服务器的基石 范范0825 ipythonlinux运维
    理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
  • 小丽成长记（四十三） 玲玲54321
    小丽发现，即使她好不容易调整好自己的心态下一秒总会有不确定的伤脑筋的事出现，一个接一个的问题，人生就没有停下的时候，小问题不断出现。不过她今天看的书，她接受了人生就是不确定的，厉害的人就是不断创造确定性，在Ta的领域比别人多的确定性就能让自己脱颖而出，显示价值从而获得的比别人多的利益。正是这样的原因，因为从前修炼自己太少，使得她现在在人生道路上打怪起来困难重重，她似乎永远摆脱不了那种无力感，有种习
  • 学点心理知识，呵护孩子健康 静候花开_7090
    昨天听了华中师范大学教育管理学系副教授张玲老师的《哪里才是学生心理健康的最后庇护所，超越教育与技术的思考》的讲座。今天又重新学习了一遍，收获匪浅。张玲博士也注意到了当今社会上的孩子由于心理问题导致的自残、自杀及伤害他人等恶性事件。她向我们普及了一个重要的命题，她说心理健康的一些基本命题，我们与我们通常的一些教育命题是不同的，她还举了几个例子，让我们明白我们原来以为的健康并非心理学上的健康。比如如果
  • 2021年12月19日，春蕾教育集团团建活动感受——黄晓丹 黄错错加油
    感受:1.从陌生到熟悉的过程。游戏环节让我们在轻松的氛围中得到了锻炼，也增长了不少知识。2.游戏过程中，我们贡献的是个人力量，展现的是团队的力量。它磨合的往往不止是工作的熟悉，更是观念上契合度的贴近。3.这和工作是一样的道理。在各自的岗位上，每个人摆正自己的位置、各司其职充分发挥才能，并团结一致劲往一处使，才能实现最大的成功。新知:1.团队精神需要不断地创新。过去，人们把创新看作是冒风险，现在人们
  • Cell Insight | 单细胞测序技术又一新发现，可用于HIV-1和Mtb共感染个体诊断 尐尐呅
    结核病是艾滋病合并其他疾病中导致患者死亡的主要原因。其中结核病由结核分枝杆菌（Mycobacteriumtuberculosis,Mtb）感染引起，获得性免疫缺陷综合症（艾滋病）由人免疫缺陷病毒（Humanimmunodeficiencyvirustype1,HIV-1）感染引起。国家感染性疾病临床医学研究中心/深圳市第三人民医院张国良团队携手深圳华大生命科学研究院吴靓团队，共同研究得出单细胞测序
  • c++ 的iostream 和 c++的stdio的区别和联系 黄卷青灯77 c++算法开发语言iostreamstdio
    在C++中，iostream和C语言的stdio.h都是用于处理输入输出的库，但它们在设计、用法和功能上有许多不同。以下是两者的区别和联系：区别1.编程风格iostream（C++风格）：C++标准库中的输入输出流类库，支持面向对象的输入输出操作。典型用法是cin（输入）和cout（输出），使用>操作符来处理数据。更加类型安全，支持用户自定义类型的输入输出。#includeintmain(){in
  • 瑶池防线 谜影梦蝶
    冥华虽然逃过了影梦的军队，但他是一个忠臣，他选择上报战况。败给影梦后成逃兵，高层亡尔还活着，七重天失守......随便一条，即可处死冥华。冥华自然是知道以仙界高层的习性此信一发自己必死无疑，但他还选择上报实情，因为责任。同样此信送到仙宫后，知道此事的人，大多数人都认定冥华要完了，所以上到仙界高层，下到扫大街的，包括冥华自己，全都准备好迎接冥华之死。如果仙界现在还属于两方之争的话，冥华必死无疑。然而
  • 爬山后遗症 璃绛
    爬山，攀登，一步一步走向制高点，是一种挑战。成功抵达是一种无法言语的快乐，在山顶吹吹风，看看风景，这是从未有过的体验。然而，爬山一时爽，下山腿打颤，颠簸的路，一路向下走，腿部力量不够，走起来抖到不行，停不下来了！第二天必定腿疼，浑身酸痛，坐立难安！
  • HQL之投影查询 归来朝歌 HQLHibernate查询语句投影查询
            在HQL查询中，常常面临这样一个场景，对于多表查询，是要将一个表的对象查出来还是要只需要每个表中的几个字段，最后放在一起显示？ 针对上面的场景，如果需要将一个对象查出来： HQL语句写“from 对象”即可 Session session = HibernateUtil.openSession();
  • Spring整合redis bylijinnan redis
    pom.xml <dependencies> <!-- Spring Data - Redis Library --> <dependency> <groupId>org.springframework.data</groupId> <artifactId>spring-data-redi
  • org.hibernate.NonUniqueResultException: query did not return a unique result: 2 0624chenhong Hibernate
    参考：http://blog.csdn.net/qingfeilee/article/details/7052736 org.hibernate.NonUniqueResultException: query did not return a unique result: 2         在项目中出现了org.hiber
  • android动画效果 不懂事的小屁孩 android动画
    前几天弄alertdialog和popupwindow的时候，用到了android的动画效果，今天专门研究了一下关于android的动画效果，列出来，方便以后使用。 Android 平台提供了两类动画。 一类是Tween动画，就是对场景里的对象不断的进行图像变化来产生动画效果（旋转、平移、放缩和渐变）。 第二类就是 Frame动画，即顺序的播放事先做好的图像，与gif图片原理类似。
  • js delete 删除机理以及它的内存泄露问题的解决方案 换个号韩国红果果 JavaScript
    delete删除属性时只是解除了属性与对象的绑定，故当属性值为一个对象时，删除时会造成内存泄露  （其实还未删除） 举例： var person={name:{firstname:'bob'}} var p=person.name delete person.name p.firstname -->'bob' // 依然可以访问p.firstname，存在内存泄露
  • Oracle将零干预分析加入网络即服务计划 蓝儿唯美 oracle
    由Oracle通信技术部门主导的演示项目并没有在本月较早前法国南斯举行的行业集团TM论坛大会中获得嘉奖。但是，Oracle通信官员解雇致力于打造一个支持零干预分配和编制功能的网络即服务（NaaS）平台，帮助企业以更灵活和更适合云的方式实现通信服务提供商（CSP）的连接产品。这个Oracle主导的项目属于TM Forum Live!活动上展示的Catalyst计划的19个项目之一。Catalyst计
  • spring学习——springmvc（二） a-john springMVC
    Spring MVC提供了非常方便的文件上传功能。 1，配置Spring支持文件上传： DispatcherServlet本身并不知道如何处理multipart的表单数据，需要一个multipart解析器把POST请求的multipart数据中抽取出来，这样DispatcherServlet就能将其传递给我们的控制器了。为了在Spring中注册multipart解析器，需要声明一个实现了Mul
  • POJ-2828-Buy Tickets aijuans ACM_POJ
    POJ-2828-Buy Tickets http://poj.org/problem?id=2828 线段树，逆序插入 #include<iostream>#include<cstdio>#include<cstring>#include<cstdlib>using namespace std;#define N 200010struct
  • Java Ant build.xml详解 asia007 build.xml
    1,什么是antant是构建工具2,什么是构建概念到处可查到，形象来说，你要把代码从某个地方拿来，编译，再拷贝到某个地方去等等操作，当然不仅与此，但是主要用来干这个3,ant的好处跨平台   --因为ant是使用java实现的，所以它跨平台使用简单--与ant的兄弟make比起来语法清晰--同样是和make相比功能强大--ant能做的事情很多，可能你用了很久，你仍然不知道它能有
  • android按钮监听器的四种技术 百合不是茶 androidxml配置监听器实现接口
    android开发中经常会用到各种各样的监听器,android监听器的写法与java又有不同的地方;    1,activity中使用内部类实现接口 ,创建内部类实例  使用add方法  与java类似   创建监听器的实例 myLis lis = new myLis();   使用add方法给按钮添加监听器  
  • 软件架构师不等同于资深程序员 bijian1013 程序员架构师架构设计
            本文的作者Armel Nene是ETAPIX Global公司的首席架构师，他居住在伦敦，他参与过的开源项目包括 Apache Lucene,，Apache Nutch， Liferay 和 Pentaho等。         如今很多的公司
  • TeamForge Wiki Syntax & CollabNet User Information Center sunjing TeamForgeHow doAttachementAnchorWiki Syntax
    the CollabNet user information center http://help.collab.net/   How do I create a new Wiki page? A CollabNet TeamForge project can have any number of Wiki pages. All Wiki pages are linked, and
  • 【Redis四】Redis数据类型 bit1129 redis
    概述 Redis是一个高性能的数据结构服务器，称之为数据结构服务器的原因是，它提供了丰富的数据类型以满足不同的应用场景，本文对Redis的数据类型以及对这些类型可能的操作进行总结。 Redis常用的数据类型包括string、set、list、hash以及sorted set.Redis本身是K/V系统，这里的数据类型指的是value的类型，而不是key的类型，key的类型只有一种即string
  • SSH2整合-附源码 白糖_ eclipsespringtomcatHibernateGoogle
    今天用eclipse终于整合出了struts2+hibernate+spring框架。 我创建的是tomcat项目，需要有tomcat插件。导入项目以后，鼠标右键选择属性，然后再找到“tomcat”项，勾选一下“Is a tomcat project”即可。具体方法见源码里的jsp图片，sql也在源码里。     补充1：项目中部分jar包不是最新版的，可能导
  • [转]开源项目代码的学习方法 braveCS 学习方法
    转自： http://blog.sina.com.cn/s/blog_693458530100lk5m.html http://www.cnblogs.com/west-link/archive/2011/06/07/2074466.html   1）阅读features。以此来搞清楚该项目有哪些特性2）思考。想想如果自己来做有这些features的项目该如何构架3）下载并安装d
  • 编程之美-子数组的最大和（二维） bylijinnan 编程之美
    package beautyOfCoding; import java.util.Arrays; import java.util.Random; public class MaxSubArraySum2 { /** * 编程之美 子数组之和的最大值（二维） */ private static final int ROW = 5; private stat
  • 读书笔记-3 chengxuyuancsdn jquery笔记resultMap配置ibatis一对多配置
    1、resultMap配置 2、ibatis一对多配置 3、jquery笔记 1、resultMap配置 当<select resultMap="topic_data"> <resultMap id="topic_data">必须一一对应。 (1)<resultMap class="tblTopic&q
  • [物理与天文]物理学新进展 comsci
          如果我们必须获得某种地球上没有的矿石,才能够进行某些能量输出装置的设计和建造,而要获得这种矿石,又必须首先进行深空探测,而要进行深空探测,又必须获得这种能量输出装置,这个矛盾的循环,会导致地球联盟在与宇宙文明建立关系的时候,陷入困境       怎么办呢?  
  • Oracle 11g新特性:Automatic Diagnostic Repository daizj oracleADR
    Oracle Database 11g的FDI（Fault Diagnosability Infrastructure）是自动化诊断方面的又一增强。 FDI的一个关键组件是自动诊断库（Automatic Diagnostic Repository-ADR）。 在oracle 11g中，alert文件的信息是以xml的文件格式存在的，另外提供了普通文本格式的alert文件。 这两份log文
  • 简单排序:选择排序 dieslrae 选择排序
    public void selectSort(int[] array){ int select; for(int i=0;i<array.length;i++){ select = i; for(int k=i+1;k<array.leng
  • C语言学习六指针的经典程序，互换两个数字 dcj3sjt126com c
    示例程序，swap_1和swap_2都是错误的，推理从1开始推到2，2没完成，推到3就完成了 # include <stdio.h> void swap_1(int, int); void swap_2(int *, int *); void swap_3(int *, int *); int main(void) { int a = 3; int b =
  • php 5.4中php-fpm 的重启、终止操作命令 dcj3sjt126com PHP
    php 5.4中php-fpm 的重启、终止操作命令: 查看php运行目录命令：which php/usr/bin/php 查看php-fpm进程数：ps aux | grep -c php-fpm 查看运行内存/usr/bin/php  -i|grep mem 重启php-fpm/etc/init.d/php-fpm restart 在phpinfo()输出内容可以看到php
  • 线程同步工具类 shuizhaosi888 同步工具类
    同步工具类包括信号量（Semaphore）、栅栏（barrier）、闭锁（CountDownLatch）   闭锁（CountDownLatch） public class RunMain { public long timeTasks(int nThreads, final Runnable task) throws InterruptedException { fin
  • bleeding edge是什么意思 haojinghua DI
    不止一次，看到很多讲技术的文章里面出现过这个词语。今天终于弄懂了——通过朋友给的浏览软件，上了wiki。  我再一次感到，没有辞典能像WiKi一样，给出这样体贴人心、一清二楚的解释了。为了表达我对WiKi的喜爱，只好在此一一中英对照，给大家上次课。   In computer science, bleeding edge is a term that
  • c中实现utf8和gbk的互转 jimmee ciconvutf8&gbk编码
    #include <iconv.h> #include <stdlib.h> #include <stdio.h> #include <unistd.h> #include <fcntl.h> #include <string.h> #include <sys/stat.h> int code_c
  • 大型分布式网站架构设计与实践 lilin530 应用服务器搜索引擎
    1.大型网站软件系统的特点？ a.高并发，大流量。 b.高可用。 c.海量数据。 d.用户分布广泛，网络情况复杂。 e.安全环境恶劣。 f.需求快速变更，发布频繁。 g.渐进式发展。 2.大型网站架构演化发展历程？ a.初始阶段的网站架构。 应用程序，数据库，文件等所有的资源都在一台服务器上。 b.应用服务器和数据服务器分离。 c.使用缓存改善网站性能。 d.使用应用
  • 在代码中获取Android theme中的attr属性值 OliveExcel androidtheme
    Android的Theme是由各种attr组合而成, 每个attr对应了这个属性的一个引用, 这个引用又可以是各种东西.   在某些情况下, 我们需要获取非自定义的主题下某个属性的内容 (比如拿到系统默认的配色colorAccent), 操作方式举例一则: int defaultColor = 0xFF000000; int[] attrsArray = { andorid.r.
  • 基于Zookeeper的分布式共享锁 roadrunners zookeeper分布式共享锁
    首先，说说我们的场景，订单服务是做成集群的，当两个以上结点同时收到一个相同订单的创建指令，这时并发就产生了，系统就会重复创建订单。等等......场景。这时，分布式共享锁就闪亮登场了。   共享锁在同一个进程中是很容易实现的，但在跨进程或者在不同Server之间就不好实现了。Zookeeper就很容易实现。具体的实现原理官网和其它网站也有翻译，这里就不在赘述了。   官
  • 两个容易被忽略的MySQL知识 tomcat_oracle mysql
    1、varchar(5)可以存储多少个汉字，多少个字母数字？ 　　相信有好多人应该跟我一样，对这个已经很熟悉了，根据经验我们能很快的做出决定，比如说用varchar(200)去存储url等等，但是，即使你用了很多次也很熟悉了，也有可能对上面的问题做出错误的回答。 　　这个问题我查了好多资料，有的人说是可以存储5个字符，2.5个汉字（每个汉字占用两个字节的话），有的人说这个要区分版本，5.0
  • zoj 3827 Information Entropy(水题) 阿尔萨斯 format
    题目链接：zoj 3827 Information Entropy 题目大意：三种底，计算和。 解题思路：调用库函数就可以直接算了，不过要注意Pi = 0的时候，不过它题目里居然也讲了。。。limp→0+plogb(p)=0，因为p是logp的高阶。 #include <cstdio> #include <cstring> #include <cmath&
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他